机器人小车焊接构架变形预测和分析
2020-09-26张金玉门志辉刘靖楠李娅娜
张金玉 门志辉 刘靖楠 李娅娜
摘要: 为探究焊接变形对机器人小车碰撞性能和使用寿命的影响,基于热弹塑性固有应变法,利用仿真软件VIRFAC对机器人小车焊接构架变形进行数值模拟。通过热源校核,模拟4种典型接头的热源分布,建立固有应变数据库,分析具有282条焊缝的机器人小车整体变形规律。结果表明:机器人小车焊接构架的最大变形为2.962 mm,位于顶层边框位置。研究结果为机器人小车的焊接设计、强度和稳定性分析提供支持。
关键词: 焊接; 构架; 热弹塑性; 固有应变; 热源校核; 变形
中图分类号: TG404; TB115.1 文献标志码: B
Abstract: To study the influence of welding deformation on the collision performance and the service life of the robot vehicle, based on the thermo-elasto-plasticity inherent strain method, the deformation of the robot vehicle welding frame is simulated in software VIRFAC. By checking with heat source, the heat source distributions of four typical joints are simulated, the inherent strain database is established, and the overall deformation rule of the robot vehicle with 282 welding seams is analyzed. The results show that the maximum deformation of the welding frame of the robot vehicle is 2.962 mm, which is located at the top of the frame. The research results can support the welding design, strength and stability analysis of the robot vehicle.
Key words: welding; frame; thermo-elasto-plasticity; inherent strain; heat source checking; deformation
0 引 言
焊接变形涉及传热学、电磁学、材料冶金学、固体力学和流体力学等,是多学科融合的复杂现象。[1]作为机械加工常用的连接方式之一,焊接在机器人小车构架的生产和制造中有重要的作用。焊接加工时往往出现残余变形,残余变形的大小直接影响机器人小车焊接构架的性能和使用寿命。焊接构架是机器人小车的关键承载部件之一,其安全性和可靠性至关重要。在机器人小车焊接构架的设计阶段,合理完善的焊接变形预测和分析需要可靠、适用的焊接变形数据支撑。
近年来,计算机技术快速发展,对焊接变形的数值仿真计算有很大地促进作用,数值模拟成为结构焊接残余应力和焊接变形预测的有效方法之一。常用的数值模拟方法有热弹塑性有限元法和固有应变法。张立平等[2]利用热弹塑性有限元法分析厚度为5 mm的Q550低碳钢薄板在对接接头焊接过程中的焊接变形;戈亮等[3]采用顺序耦合热弹塑性有限元法对自由状态下的甲板分段焊接过程进行数值模拟;纪浩然[4]采用热弹塑性有限元法分析大型复杂结构的焊接变形;于红等[5]采用固有应变法研究高速列车司机室前窗框的焊接变形;唐琪等[6]通過有限元软件SYSWELD,采用固有应变法计算不同焊接顺序时枕梁的焊接变形,分析焊接顺序对枕梁焊接变形的影响;李树栋等[7]采用固有应变法对不锈钢车体的车顶进行焊接变形仿真;VISHVESHA等[8]采用固有应变法预测汽轮机导叶座外圈的焊接变形;王小杰等[9]采用固有应变法研究不同焊点距离对门槛结构焊接变形的影响;王素节等[10]采用热弹塑性法预测T型梁的焊接变形。目前,针对机器人小车焊接构架变形预测和分析的文献很少。
本文以机器人小车焊接构架为研究对象,基于热弹塑性固有应变法,利用有限元分析和VIRFAC软件,结合实际加工工艺,对机器人小车构架焊接变形进行仿真分析,为机器人小车焊接构架的可靠性设计提供技术参考。
1 基本原理
1.1 固有应变法
固有应变法最初由日本学者提出。固有应变是指热循环后残留在构件内引起构件残余应力和变形的应变,也称为残余应变。固有应变是焊件产生应力和变形的根本原因。固有应变表示构件从应力状态剥离后处于自由状态时,与基准状态对比所具有的应变。固有应变包括塑性应变、热应变和相应变,其表达式为ε*=εP+εT+εX(1)式中:εP为塑性应变;εT为热应变;εX为相应变。
若只经过1次热循环,则构件热应变基本可以忽略不计,构件材料为低碳钢,也可以不考虑相应变,所以固有应变可以用塑性应变代替,即ε*=εP(2)
1.2 热弹塑性固有应变法
目前,基于固有应变理论进行焊接变形仿真主要有2种方法:一种是基于经验数据的固有应变法,另一种是基于热弹塑性的固有应变法。本文采用基于热弹塑性的固有应变法。
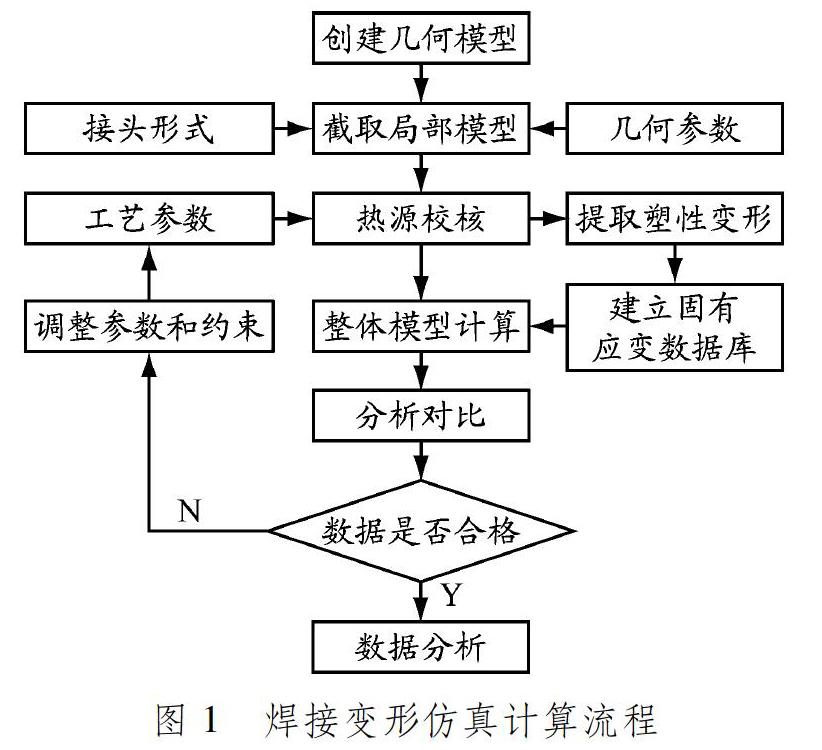
首先,利用热弹塑性有限元法对机器人小车焊接构架的局部模型进行仿真和计算;然后,提取塑性应变并建立固有应变数据库;最后,将固有应变作为初始应变,施加到焊缝及其附近区域,进行1次弹性计算,得到机器人小车焊接构架的最终应变。焊接变形仿真计算流程见图1。
2 焊接构架模型
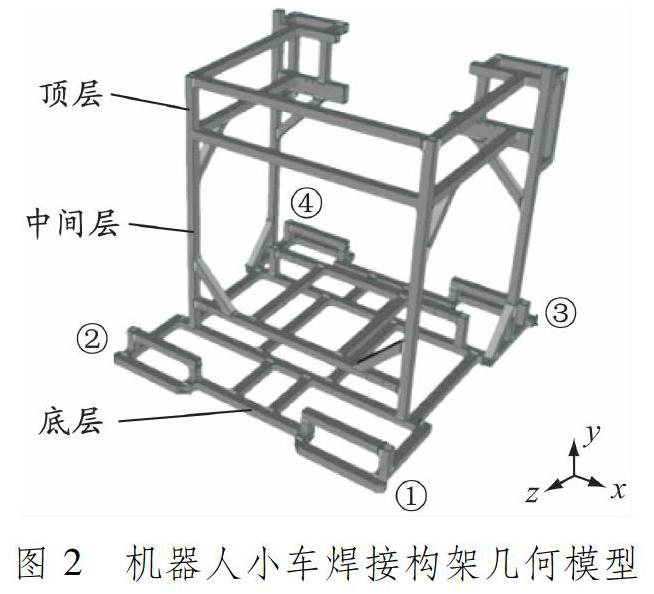
目前,大部分机器人小车焊接构架分为底层、中间层和顶层等3部分,由方形钢管焊接而成,方形钢管的母材材料为Q345A,焊接构架几何模型见图2。机器人小车焊接构架主要起支撑和保护作用,因此需要研究构架中282条焊缝对机器人小车整体焊接构架的影响。
3 局部模型热源校核
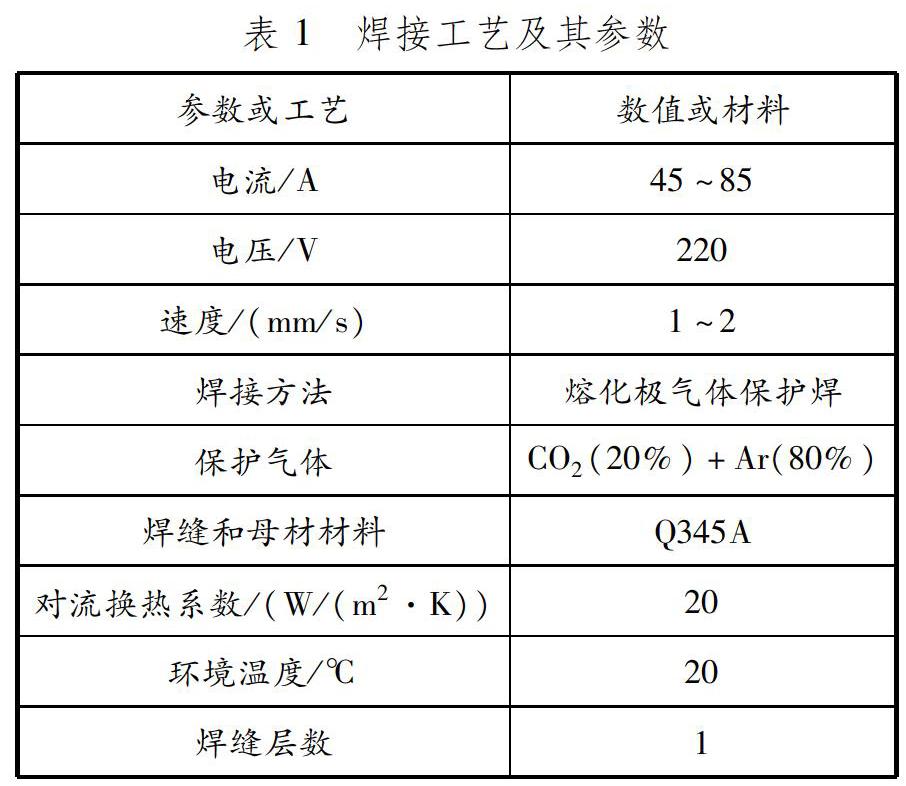
根据不同焊接接头形式,可将机器人小车焊接构架的接头分为4类,局部接头和焊缝填充物均用六面体实体单元模拟。焊接工艺及其参数见表1。
热源校核是焊接仿真和计算的关键步骤,其准确性直接影响固有应变数据库的准确性。局部接头仿真时,热源采用Goldak双椭球体热源,局部焊接接头热源校核示意见表2。
4 边界条件
4.1 约束条件
取方形钢管厚度为1 mm、方形截面边长为2 cm。考虑模型的最小夹持条件,约束底层4个点防止刚体移动。机器人小车的装夹约束条件(见图2)为:①点约束x、y和z方向,②点约束y和z方向,③点约束x和y方向,④点约束y方向。
4.2 焊接顺序
机器人小车焊接构架按照从底层到顶层的顺序依次焊接。底层焊接顺序见图3。底层按照空心箭头所指顺序从中间向两端焊接,每个横杆都先焊接内侧再焊接外侧。中间层焊接顺序见图4。中间层先焊接前面的短竖杆及其上面的横杆,再绕y轴逆时针顺序焊接4根长竖杆;中间部分先焊接竖杆再焊接横杆;最后焊接具有固定作用的斜杆。
顶层焊接顺序见图5。顶层有2层:下面一层先按照逆时针顺序依次焊接3根横杆,然后焊接长方形端口构件,最后按照逆时针方向焊接4根斜杆将其固定;上面一层同样也按逆时针方向先焊接竖杆再焊接横杆。最外侧突出结构先焊接支撑杆再焊接连接杆。
5 整体模型计算和结果分析
5.1 固有应变的提取和数据库建立
由局部接头焊缝应变结果的范围可确定焊缝局部塑性应变的提取半径。根据应变分布规律,选取包含固有应变区域的单元最大直线距离,即为焊缝塑性应变提取半径。通过设置焊接起弧阶段和焊接收弧阶段占焊缝长度的百分比确定所需提取的固有应变。提取局部接头长度前25%的塑性应变作为焊接起弧阶段的固有应变,提取局部接头长度后25%的塑性应变作为焊接收弧阶段的固有应变,提取局部接头中间50%的塑性应变作为焊接稳定阶段的固有应变,最后生成局部接头塑性应变数据库文件。本文提取局部接头焊缝处各方向的塑性应变建立固有应变数据库,再将固有应变数值分别映射到整体模型的每条焊缝,进行数值模拟。
5.2 整体模型计算结果分析
利用局部焊缝的塑性应变作为映射源,对整体模型的每条焊缝进行映射和1次弹性计算。机器人小车构架焊接工艺方案的整体变形见图6。
机器人小车焊接构架底层和中间层的变形不大,整体最大变形位于构架顶层边框位置,最大变形为2.962 mm,x、y和z方向最大变形依次为0.730、0.465和2.655 mm,相对于整个焊接构架,焊接变形较小。对实验室十几台模型车的焊接变形进行测量统计,x、y方向的变形较小,z方向的变形约为3 mm,模拟数据与试验数据基本吻合,计算结果可为 机器人小车构架焊接变形优化设计和分析提供数据支持。
6 结 论
通过对机器人小车焊接构架进行焊接变形预测和分析,得出以下结论:
(1)将焊接构架局部接头分为4种类型,根据实际焊接工艺参数,对每种接头进行热源校核,热源校核计算结果合理。
(2)在热源校核基础上,提取每个接头各主方向的塑性应變建立固有应变数据库,为整体模型的弹性计算提供数据来源。
(3)利用固有应变数据库进行机器人小车焊接构架整体变形仿真计算,整体模型网格为2 909 266个,焊缝为282条,最大焊接变形为2.962 mm,位于构架顶层边框位置。
通过提取局部接头各方向塑性应变,建立固有应变数据库,再将固有应变映射到整体模型的每条焊缝进行模拟计算。这种方法可将百万量级网格、几百条焊缝模型的焊接变形计算时间缩短至十几个小时。因此,基于热弹塑性的固有应变法经济适用,可以应用于结构比较复杂的机器人小车焊接构架的变形仿真和计算。
参考文献:
[1] 谢超. 钢桥典型构造焊接残余应力有限元分析[D]. 成都: 西南交通大学, 2017.
[2] 张立平, 纪昂, 陈明刚, 等. 应变模型对薄板面外变形的影响[J]. 热加工工艺, 2019, 48(5): 241-244. DOI: 10.14158/j.cnki.1001-3814.2019.05.061.
[3] 戈亮, 刘序辰. 基于热弹塑性计算分析的甲板分段建造反变形值设置方法[J]. 造船技术, 2018(6): 59-63. DOI: 10.3969/j.issn.1000-3878.2018.06.014.
[4] 纪浩然. 大型复杂结构焊接变形热弹塑性有限元分析[J]. 中国金属通报, 2019(3): 136. DOI: 10.3969/j.issn.1672-1667.2019.03.085.
[5] 于红, 韩士宏, 田慧. 基于固有应变法的高速列车司机室前窗框焊接变形研究[J]. 焊接技术, 2019, 48(8): 13-15. DOI: 10.13846/j.cnki.cn12-1070/tg.2019.08.004.
[6] 唐琪, 刘赞, 陈鹏, 等. 基于固有应变法的地铁枕梁焊接变形数值模拟[J]. 热加工工艺, 2019, 48(19): 128-130. DOI: 10.14158/j.cnki.1001-3814.2019.19.032.
[7] 李树栋, 祝航, 戴忠晨, 等. 基于固有应变法的不锈钢车体车顶焊接变形仿真[J]. 电焊机, 2018, 48(8): 9-12. DOI: 10.7512/j.issn.1001-2303.2018.08.02.
[8] VISHVESHA A, PANDEY C, MAHAPATRA M M, et al. On estimation and control of welding distortion of guide blade carrier for a 660 MW turbine by using inherent strain method[J]. International Journal of Steel Structures, 2017, 17(1): 53-63. DOI: 10.1007/s13296-016-0098-4.
[9] 王小杰, 韩振宇, 刘春景, 等. 基于固有应变法的超高强钢电阻点焊变形研究[J]. 焊接技术, 2019, 48(10): 26-28. DOI: 10.13846/j.cnki.cn12-1070/tg.2019.10.006.
[10] 王素节, 马颖珊, 史良宇, 等. 钢制薄板T型梁焊接变形及焊接残余应力数值仿真[J]. 机械研究与应用, 2019, 32(6): 1-4. DOI: 10.16576/j.cnki.1007-4414.2019.06.001.
(编辑 章梦)
