道砟胶固化道床力学特性的离散元分析
2020-09-26孙倩孙文芳李勇俊季顺迎
孙倩 孙文芳 李勇俊 季顺迎


摘要: 为探究道砟胶的使用对有砟轨道道床的影响规律,采用镶嵌式组合颗粒单元构造道砟颗粒,根据相关文献确定道砟胶的黏结模型和刚度模型,利用单轴压缩试验和三点弯曲试验确定道砟胶固化道床的细观力学参数,基于离散元法对道砟胶固化道床开展数值模拟,系统分析道砟胶用量和加胶深度对道砟胶固化道床力学特性的影响。模拟结果表明:随着道砟胶加入量的增大,道床的累积沉降量减小且累积沉降量的振幅减小,道床的刚度逐渐增大且增大趋势逐渐趋于平缓;当道砟胶加入量为48 kg/m3时,道床的累积沉降量最小且刚度最大;随着道砟胶加入深度的增大,道床的累积沉降量减小且累積沉降量的振幅减小,道床的刚度与道砟胶加入深度呈线性关系;道床全部加入道砟胶时道床的沉降量最小且刚度最大。
关键词: 道砟胶; 固化剂; 道床; 离散元法; 镶嵌式组合颗粒; 沉降量
中图分类号: U214.2;TB115.2 文献标志码: B
Abstract: To study the influence of ballast glue on ballast track bed, the ballast glue curing track bed is simulated using discrete element method, and the influence of the consumption and depth of ballast glue on the mechanical properties of ballast glue curing track bed is analyzed. The ballast particles are constructed with mosaic composite particles. The bond model and stiffness model of ballast glue are determined according to relevant literature. The micromechanical parameters of ballast glue curing track bed is determined by uniaxial compression test and three-point bending test. The simulation results show that, with the increase of ballast glue consumption, the cumulative settlement of track bed decreases, and the amplitude of cumulative settlement decreases, and the rigidity of track bed increases gradually and its increasing trend tends to be slow; the cumulative settlement is minimum and the track bed rigidity is maximum when the consumption of ballast glue is 48 kg/m3; with the increase of ballast glue depth, the cumulative settlement of track bed decreases and the amplitude of cumulative settlement decreases, and there is a linear relationship between the rigidity of track bed and the depth of ballast glue; the settlement of the track bed is the minimum and the rigidity is the maximum when whole track bed are added with ballast glue.
Key words: ballast glue; curing agent; track bed; discrete element method; mosaic composite particle; settlement
0 引 言
道砟胶是以多种胶结材料(含活泼氢的多醇、聚氨酯、二邻氯二苯胺甲烷等)[1]制备的新型环保型材料。道砟胶的加固形式主要包括表面胶结和结构胶结。表面胶结喷射道砟胶厚度为4~7 cm,可防止道砟飞溅,改善道床表面清洁度,保持道砟道床(尤其是砟肩)的几何形状。结构胶结喷射道砟胶厚度为10~25 cm,用于道床过渡段刚度调整,可提高道床结构安全性、增强道床稳定性、提高小半径曲线处的横向阻力、固定道砟边坡并增强稳定性。[2]在德国,道砟胶被用于相邻线路改造时稳定道床和保持道床的清洁度,以及有砟、无砟道床间的平稳过度;在比利时,道砟胶被用于稳定高架桥砟肩道床;在匈牙利,道砟胶被用于减少道砟的破碎。近年来,随着高速铁路的不断发展,我国也开始使用道砟胶,但对道砟胶的研究还处于试验研究和工程应用方面,对道砟胶与道砟的微观相互作用的研究还不够充分。
对于道砟胶的试验研究,国内外学者主要运用现场施工和实验室中施加循环载荷2种方法[3-6],对比分析不同道砟胶用量[7]、全黏结断面、部分黏结断面和局部黏结断面[8]等情况下,道床支撑刚度的横纵向阻力与位移的关系。这些试验研究只是进行宏观分析,对道砟与道砟胶微观力学特性的研究很少。KEENE等[9]和蒋函珂[10]运用有限元软件建立道砟胶固化道床动力学仿真模型,但对道砟胶材料研究较少,缺乏合适的仿真参数导致数据不够准确。XIAO等[11]采用离散元法将枕木和道床分别离散成等径的球体颗粒进行数值模拟,但由于道砟的真实形状并非球形而是不规则的几何体,因此模拟不够真实。井国庆等[12]和胡飞[13]采用多个圆球叠加形成颗粒簇,真实描述实际铁路道砟颗粒形状和大小,但是没有考虑适合道砟胶的黏结模型。
本文基于离散元法,采用镶嵌式组合颗粒单元对道砟进行模拟。因为道砟胶固化后的形态特殊,所以参考相关文献,黏结模型运用2种临界状态的液-固体积比和道砟胶柱面半径进行拟合获得,刚度模型采用水泥沙连续黏结模型获得。通过单轴压缩和三点弯曲试验,校准离散元模型的力学计算参数,得到准确可靠的道砟胶黏结强度和摩擦因数。对道砟胶固化道床开展数值模拟,系统分析道砟胶用量和加胶深度对道砟胶固化道床的动力学响应。分析在循环往复载荷下,不同道砟胶用量和加胶深度的道砟胶固化道床的整体刚度和累积沉降量。采用离散元数值模拟的方法,分析道砟胶固化道床的动力过程,更好地揭示其内部变形机理。
1 道砟胶固化道床的离散元模型
1.1 道砟颗粒的单元构造
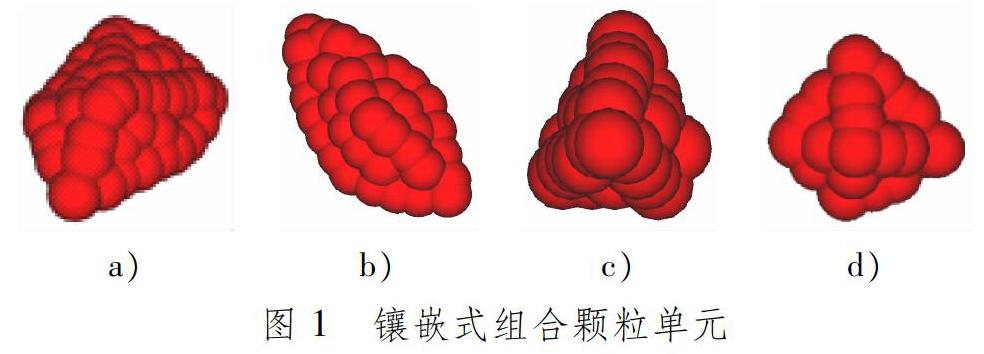
道砟为具有一定棱角的非规则多面体结构。针对道砟颗粒的特殊几何形态,采用镶嵌式组合颗粒单元构造道砟颗粒,见图1。根据道砟碎石有效粒径的随机性,构造道砟的颗粒尺寸为25~63 mm。运用有限分割法获得组合颗粒的质量、质心和转动惯量,并采用四元素法将组合颗粒的动力学分量在整体坐标系与局部坐标系下进行转换。[14]组成镶嵌模式单元的内部颗粒粒径不同,可根据设定的颗粒形态任意组合,使形态更加真实。该非规则颗粒构造可以更好地研究道砟的细观结构对道砟胶固化道床的影响。
1.2 道砟胶固化道床的黏结模型
向道砟中加入道砟胶的过程可分为干燥状态、钟摆状态、悬索状态、毛细血管状态和泥浆状态等5种状态[15],见图2。干燥状态到钟摆状态为加胶量较少的状态。在没有固化前,道砟胶性质与液桥类似,所以类比液桥模型分析道砟胶,此时2个球体间道砟胶的几何参数见图3。
道砟胶的体积是决定断裂能大小的重要因素,也是控制2个道砟颗粒连接的关键,对颗粒的分离和凝聚起决定性作用。道砟胶柱面直径与液-固接触角、道砟胶的体积和道砟颗粒间的距离密切相关。2个球体颗粒半径越大,道砟颗粒间胶结的体积越大,因此道砟胶的体积(用量)取决于2个球体的半径。RABINOVICH等[16]将理论与试验融合,推理得到等径球体颗粒间道砟胶的液-固接触角α,同时引入等效颗粒半径,将公式推广至不等径球体颗粒,α的定义为α=2HRVπRH2+1-1
(1)式中:H为2个球体间的距离;R为等效颗粒半径;V为球形颗粒间道砟胶的体积。此公式的适用范围为α<1,即道砟胶用量较少的情况,此时2个颗粒的等效半径为R=2R1R2(R1+R2)
(2) 在此状态下,道砟胶的柱面半径Rb=Rsin α,道砟胶的体积V=πα4R34+πα2R2H,此时液-固体积比V*=3V/8πR3,可求得V*=3α432+3Hα28R。
當道砟胶加入量增大时,道砟胶的形态为由钟摆状态至悬索状态,此过程的临界状态为平行黏结状态(见图4),此时Rb=R,道砟胶的体积V=πR2×(2R+H)-4πR33,因此液-固体积比V*=14+3H8R。
当液-固接触角α>1即加胶量较多时,需要推导道砟胶柱面半径Rb。在初始状态下,液-固体积比V*与道砟胶柱面半径Rb的关系曲线见图5。
在道砟受力过程中,道砟胶发生形变,2个球体间的距离H与道砟胶柱面半径Rb的关系曲线见图6。
将同样的道砟与道砟胶混合物制成200 mm×200 mm×400 mm的长方体试样,进行单轴压缩试验[9],试验加载示意见图9。利用此装置以0.843 MPa/s的名义应力率进行加载,获得试样的压缩强度为2 607 kPa。
2.2 数值模拟
分别构造与单轴压缩和三点弯曲试验试样尺寸相同的长方体试样模型,进行数值模拟,见图10。道砟胶摩擦因数取0.3、黏结强度取2.5 MPa,模拟试验获得试样应力随时间变化的曲线,见图11。单轴压缩试验和三点弯曲试验曲线的峰值分别对应试样的压缩强度和弯曲强度。
由此可知,试样的单轴压缩破坏强度σc=2 607 kPa、三点弯曲破坏强度σf=938 kPa,代入拟合公式,可得到摩擦因数μ=0.105,此时道砟胶的黏结强度σb=2.24 MPa。
3 道砟胶固化道床数值模拟
3.1 道砟胶固化道床试验离散元模拟参数
把混合道砟放入道砟试验箱模拟道床,对道床施加循环往复载荷,分析道砟胶固化道床的力学特性。模拟试验箱模型尺寸为600 mm×300 mm×400 mm,道砟颗粒为793块,见图13。
道砟胶固化道床离散元数值模拟计算参数见表1。道砟随机下落至道砟箱中,道砟夯实稳定后加入道砟胶。对道砟箱上方的枕木缓慢施加载荷,最小载荷为5.5 kN,最大载荷为30.5 kN,加载频率为3.0 Hz。
3.2 循环载荷下道床的累积沉降量
取道砟胶加入量为6 kg/m3,对枕木施加35次往复循环载荷,获得道床循环受力载荷P与累积沉降量s的关系,见图14。道床的累积沉降量与载荷的变化规律相似,呈现周期性循环。第一次循环,道床的沉降量较大;随着加载次数的增多,道床的累积沉降量趋于平稳。这是因为初始阶段道砟排列松散,随着循环载荷的施加,道砟发生错动而排列紧密、空隙缩小,使得道床累积沉降量增长减缓。
3.3 道砟胶加入量对道床的影响
分别取道砟胶加入量为0、6、12、24和48 kg/m3,对枕木施加从5.0 kN均匀增加至30.0 kN的载荷,进行离散元计算,得到道床的累积沉降量s和整体刚度K,见图15。由此可知,加入48 kg/m3道砟胶时道床的整体刚度为51.311 N/m,不使用道砟胶时其刚度为32.742 N/m,前者是后者的1.567倍。可见,加入道砟胶可以有效提高道床的整体刚度;随着道砟胶加入量的增大,道床刚度增大且增势逐渐趋于平缓。
对枕木施加循环载荷,计算道砟胶加入量分别为0、6、12、24和48 kg/m3时道床的累积沉降量,见图16a,并由此得到10个加载周期后道床的累积沉降量,见图16b。随着道砟胶加入量的增大,道床的累积沉降量变小且逐渐趋于稳定;道砟胶加入量为48 kg/m3时道床的最大累积沉降量为0.557 mm,不使用道砟胶时的最大累积沉降量为1.322 mm,前者仅为后者的42.1%。随着道砟胶用量增多,道床累积沉降量的振幅减小。因为作用在道砟上的载荷相同,所以振幅减小说明刚度增大,验证道床整体刚度随道砟胶加入量增大而增大这一规律。
3.4 道砟胶加入深度对道床的影响
取道砟胶加入量为48 kg/m3,分别将道砟胶加入不同深度的道砟中,对枕木施加从5.0 kN均匀增加至30.0 kN的载荷,进行离散元计算。加胶道砟深度分别取不使用道砟胶(即深度为0)、由上至下约1/3(即D=1/3)道砟加入道砟胶、由上至下约2/3(即D=2/3)道砟加入道砟胶、全部(即D=1)加入道砟胶4种情况,计算得到的道床累积沉降量和刚度见图17。由此可知,上部1/3道砟加入道砟胶时道床的刚度为36.975 N/m,上部2/3道砟加入道砟胶时道床的刚度为44.785 N/m,全部加入道砟胶时道床刚度为51.311 N/m。可见,道砟胶可有效提高道床的整体刚度,且道砟胶加入的深度与道床刚度约呈线性关系。
对上述4种道床上的枕木施加循环载荷,对比分析10个循环周期内道床的累积沉降量,并整理10个加载周期后道床的最大累积沉降量,见图18。由上至下1/3道砟加入道砟胶时道床的最大累积沉降量为0.842 mm,2/3道砟加入道砟胶时道床的最大累积沉降量为0.694 mm,全部加入道砟胶时道床的最大累积沉降量最小,由此可见道砟胶加入深度对道床的累积沉降量有明显作用。由图18还可以发現,道砟胶加入的深度越大,道床累积沉降量的振幅越小。因为作用在枕木上的载荷相同,所以道床累积沉降量振幅减小说明道床刚度增大,也可验证道床刚度随道砟胶加入深度增大而增大这一规律。
4 结 论
采用镶嵌式组合颗粒单元构造非规则形态的道砟颗粒,研究道砟胶加入量与加胶深度对道床累积沉降量和刚度的影响规律。模拟道砟的真实工作状态,探究在往复载荷下道床的沉降过程,得到结论如下:
(1)道砟胶固化道床离散元模型的细观参数无法通过试验直接获得,因此对混合道砟试样进行单轴压缩强度试验和三点弯曲强度试验,计算得到道砟胶的黏结强度为2.24 MPa、摩擦因数为0.15。
(2)随着道砟胶加入量增大,道床累积沉降量逐渐减小、累积沉降量的振幅逐渐减小、整体刚度逐渐增大且增大趋势趋于平缓。当道砟胶加入量为48 kg/m3时,道床的累积沉降量最小且刚度最大。
(3)随着道砟胶加入深度增大,道床累积沉降量减小,累积沉降量的振幅减小,道床整体刚度增加且与加胶深度大致呈线性关系,全部加入道砟胶时道床的累积沉降量最小且刚度最大。
(4)由模拟数据可知,道砟胶固化道床稳定性更强,能够更好地维持轨道形状,推荐在有砟轨道上广泛使用。
参考文献:
[1] 张亮. 高速铁路用道碴胶的制备与应用[J]. 中国胶粘剂, 2010, 19(9): 46-49.
[2] 朱永见. 聚氨酯在铁路道砟黏结技术中的应用综述[J]. 铁道标准设计, 2016, 60(10): 31-35. DOI: 10.13238/j.issn.1004-2954.2016.10.008.
[3] KENNEDY J, WOODWARD P K, MEDERO G, et al. Reducing railway track settlement using three-dimensional polyurethane polymer reinforcement of ballast[J]. Construction and Building Materials, 2013, 44: 615-625. DOI: 10.1016/j.conbuildmat.2013.03.002.
[4] WOODWARD P K, ABDELLAHEL K, LAGHROUCHEO, et al. Application of polyurethane geocomposites to help maintain track geometry for high-speed ballasted railway tracks[J]. Journal of Zhejiang University SCIENCE A: Applied Physics & Engineering, 2012, 13(11): 836-849. DOI: 10.1631/jzus.A12ISGT3.
[5] 朱永见. 道砟胶应用于有砟-无砟轨道过渡段的关键控制技术[J]. 铁道建筑, 2016(8): 133-136. DOI: 10.3969/j.issn.1003-1995.2016.08.33.
[6] 朱永见, 亓伟, 陈攀. 道砟胶对过渡段道床参数的影响规律研究[J]. 铁道科学与工程学报, 2016, 13(1): 35-38.
[7] 刘晓阳, 刘浩. 道砟胶对加强道床刚度的作用[J]. 中国西部科技, 2013, 12(5): 14-15. DOI: 10.3969/j.issn.1671-6396.2013.05.007.
[8] 亓伟. 道砟胶固化道床技术在有砟-无砟轨道过渡段的应用[J]. 中国铁路, 2016(12): 47-51.
[9] KEENE A, EDIL T, FRATTA D, et al. Modeling effect of polyurethane stabilization on rail track response[C]// Proceedings of Geo-Congress 2013. San Diego: American Society of Civil Engineers. DOI: 10.1061/9780784412787.141.
