基于多尺度卷积神经网络的立体匹配算法研究

段中兴，齐嘉麟

(1.西安建筑科技大学 信息与控制工程学院，西安 7100652.西部绿色建筑国家重点实验室，西安 710065)

0 引言

21世纪以来，机器人在各个行业都得到了迅速的发展，如艰难环境的探索任务、无人机自主导航和三维立体建模[1]。在建筑行业，建筑工地中钢筋水泥的抓取与搬运，往往采用人力的搬运，但是由于受到体力和环境条件的限制，使得整个工作过程效率太低，一些恶劣天气时更会拖延工期甚至对工人的生命安全也难以保障。机器人作为现代文明的重要产物，也越来越多的用于建筑工地中。作为移动机器人系统中最重要的一环，双目视觉系统成为了越来越多学者研究的热门话题。双目立体视觉通过模仿人的双目，经过立体匹配算法可以获得目标的视差信息从而获得目标的深度信息，这种方法已经应用于各种场合，如目标识别与跟踪、自主导航等。

根据现有的研究，立体匹配算法可以分为局部算法和全局算法。在局部算法中，两个像素之间的匹配代价是通过局部计算每个像素的一个支持窗口(例如9×9)，并且通常会通过聚合基于像素的匹配代价来进行隐式平滑假设。通过聚合匹配代价来计算最优视差。传统的局部算法包括平方差之和算法(SSD)、绝对误差和算法(SAD)和基于灰度值的归一化互相关算法[2](NCC)。与全局算法相比，局部算法通常速度更快，但由于局部算法的有限性，因此准确性较低。相反，全局算法做出明确的平滑假设，并通过解决基于能量的优化问题来搜索最优视差。目前常用的全局方法包括基于动态规划[3]，置信度传播[4]和图割[5]的全局计算方法。尽管这些全局算法取得了较好的实验结果，但是同时也需要复杂的计算以及庞大的计算量。目前，很多学者在立体匹配算法的研究中取得了一定的成果。文献[6-7]提出了一种基于树形结构代价聚合的非局部立体匹配算法(Non-Local Filter，NLF)，在代价聚合阶段利用目标的颜色信息求解最优视差；文献[8]提出了一种半全局立体匹配算法(Semi-Glob Matching，SGBM)，SGBM也基于构造全局代价函数，但是它沿8个方向执行优化，SGBM取得了较高的准确性，而计算复杂度相比全局算法却低得多，但是相比局部算法，在一些实时性要求较高场合仍有待提高。

由于建筑工地环境往往存在遮挡物以及室外环境受光照影响较大，现有立体匹配算法往往不能达到最佳的匹配效果，计算获得的视差图在光照变化大、纹理较弱以及深度不连续区域的误匹配点较多。研究表明，卷积神经网络(Convolutional Neural Network，CNN)凭借其可以有效获取目标深层次特征的能力，主要应用于自然语言处理、图像识别和视频领域等[9-10]，近年来，在立体匹配算法中也取得了实质性的发展[11]。Zbontar等人[12]立体匹配算法中，利用CNN计算图像的匹配代价，相较传统算法提高了视差图精度，但是未考虑到目标图的多尺度信息；文献[13]提出了一种基于图像金字塔思想的方法，将原图经过多次降采样后的子图输入网络，提高了视差图精度，但是计算复杂度太高。

针对以上方法存在的优缺点，本文提出了一种基于多尺度卷积神经网络的立体匹配算法。第一步，在各个尺度上，通过不同卷积核实现图像的特征提取，构建了一种具有多尺度的CNN模型来计算匹配代价；第二步，利用半全局立体匹配算法的思想，建立全局能量函数，利用动态规划的思想在不同方向上执行优化搜索最佳视差；第三步，利用左右一致性检测对得到的视差图中的遮挡点进行处理，进行进一步优化与校正，最终生成精度较高的视差图。

1 基于多尺度卷积神经网络的立体匹配

1.1 基于CNN的立体匹配算法

CNN结构主要有由输入层、卷积层、池化层、全连接层和输出层组成。卷积层实现对目标特征提取，利用多个卷积核提取多角度的空间信息。池化层在保留主要特征的同时减少参数和计算量，防止过拟合，提高模型泛化能力。全连接层出现在最后一层，主要对卷积层和池化层所提取的特征做加权。

本文基于CNN的立体匹配整体分为两步，第一步为网络训练，第二步为视差计算，算法流程如图1所示。

图1 基于CNN的立体匹配流程

1.2 多尺度卷积

Siamese Networks[14]架构是双目视觉中立体匹配最常用的结构之一，如图2所示。输入为双目相机拍摄经坐标变换后的原始左右标准图像块，经过多个卷积和全连接过程后就可以得到图像的匹配代价。由于双目相机采集到的障碍物目标的尺度大小不一，并且多数存在光照变化大、纹理过渡区域不明显和深度不连续的问题。本文设计了一种基于多尺度CNN网络结构，如图3所示。

图2 Siamese Networks的一般结构

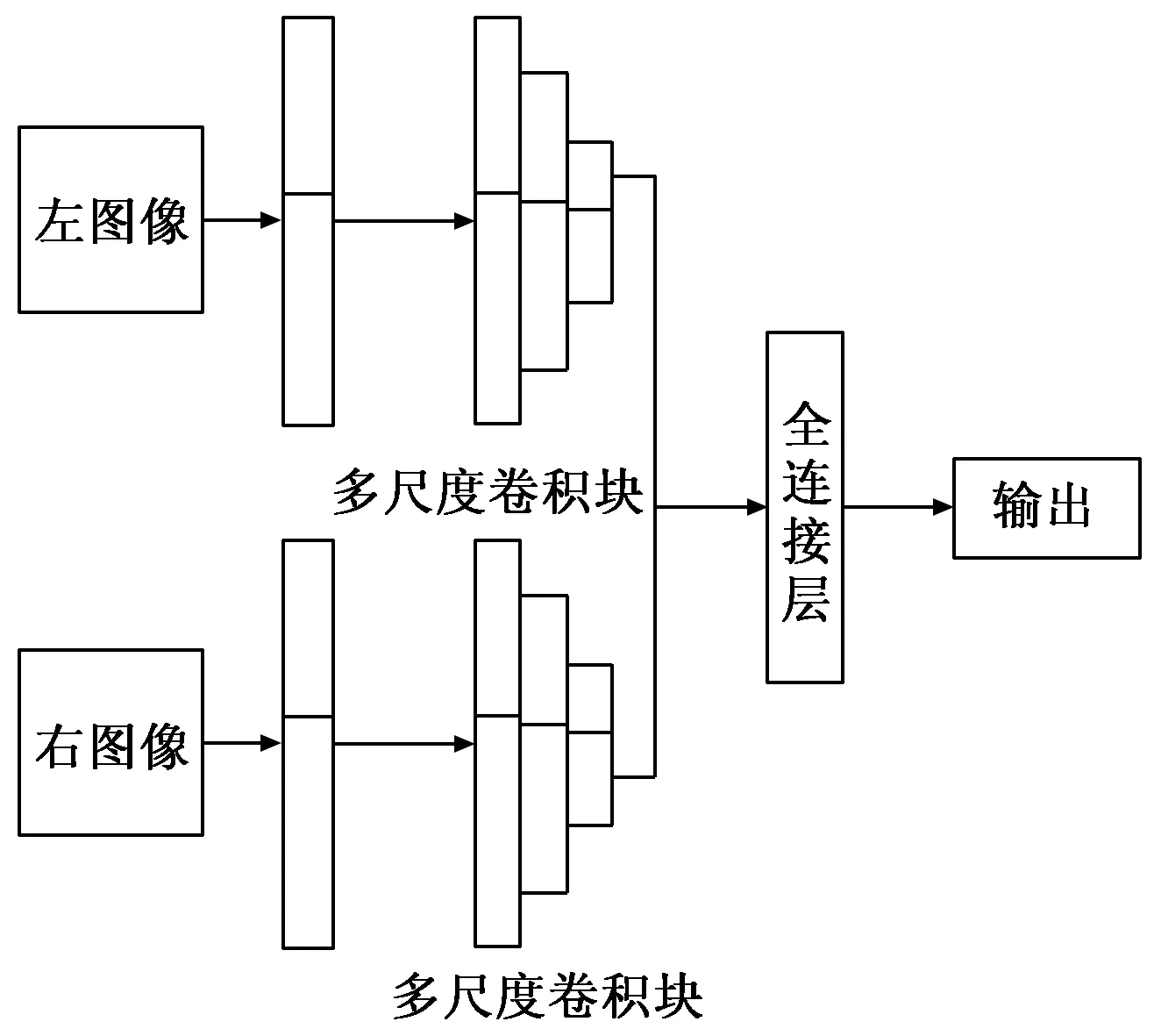
图3 本文的网络结构

在该网络结构中，利用多尺度卷积神经网络(Multi-Scale Convolutional Neural Network，MSCNN)的思想，采用多尺度卷积块(Multi-Scale Block，MSB)，从图像中学习与尺度相关的特征，实现对同一障碍物对象提取不同尺度上的特征信息，其具体结构如图4所示。

图4 多尺度卷积块

在多尺度卷积神经网络中，多尺度卷积块利用4个并列不同大小的卷积核来获取目标的尺度信息，本文经过实验发现，采用1×1、3×3、5×5和7×7的卷积核可以更好的从局部特征获得上下文语义信息并减少参数数量。

1.3 损失函数

L是双目立体匹配算法中Siamese结构常用的损失函数，和其他模型不同，它的输出代表两个向量的相似程度，如式(1)所示：

L=(1-y)·γ(p,q)+y·max{0,m-γ(p,q)}

(1)

式中，p和q分别代表左图和右图中的某一像素点；γ(p,q)为神经网络的输出，代表分别以p和q为中心的图像块的相似程度；y为训练时的标签值，当左右图中的图像块匹配正确，即为正例时，取1，反之，为反例时取0；m代表边界值。然而，在训练时，该式对每个样本都进行反向传播调整参数，导致训练过程繁琐增加了训练时间。本文在此基础上进行了改进，给出了一种新的损失函数，使模型在训练时的收敛速度加快。式(2)为本文所用的损失函数：

L=max{0,m-γ+(p,q)+γ-(p,q)}

(2)

式中，γ+(p,q) 代表左右两图中的图像块匹配正确(正例)时的输出，γ-(p,q) 代表左右两图中的图像块匹配错误(负例)时的输出。该损失函数在训练时由一正一负两个样本同时进行训练，加快模型收敛速度，并且去掉原有损失函数中的标签值，样本不再拥有确切的标签，提高模型的鲁棒性和拓展性。根据实验，本文将边界值m设为1。该损失函数可以提高匹配正确图像的相似度，并降低匹配错误图像的相似度。

2 基于多尺度CNN结构的匹配代价计算

采用监督学习的方法在本文所设计的网络结构上对标准立体匹配图像进行训练，训练好的模型用于计算匹配代价。同时，对训练使用的图像进行翻转、裁剪等操作，加入训练样本中，使模型训练更加充分。

由于立体匹配算法所使用的均为经过相机标定后的标准双目图像，所以图像中对应的像素点均位于同一水平线上。在左图中提取以像素点p为中心的一个图像块，同时提取以右图中对应视差为d的像素点p-d为中心的图像块，利用训练好的网络，计算输出结果。计算得到的匹配代价如式(3)：

(3)

3 代价聚合

由多尺度卷积模型计算得到的匹配代价计算只考虑到了图像的局部关联，视差图含有的噪声较多，无法直接用来获取目标的最优视差值，所以代价聚合就显得尤为重要。

为了提高立体匹配的精度，本文构造了一个全局能量函数，将式(3)获得的初始匹配代价作为数据项；其次，构造正则化约束，也称平滑项[16]：若相邻两像素点的视差值相差1，给定惩罚因子P1；若大于1，给定P2。本文构造的能量函数如公式(4)所示：

(4)

式中，p为图中任一像素点，q为其相邻像素点；T为截断函数，当括号中函数值为真时，取1；反之，取0。

由于目标图像是二维的，采用动态规划在目标视差图中求解最优视差值是一个NP难的问题。本文将二维图像上的最优问题分解为4个方向上的一维问题，利用动态规划的方法求解每个一维问题上的最优解，如式(5)所示：

Lr(p,d)=

(5)

式中，r表示指向像素点p的方向；p-r表示在r方向上p的上一个像素点；Lr(p,d)表示像素点p在方向r上视差为d的匹配代价。同时，为了防止匹配代价溢出，像素点p的匹配代价需减去像素点p-r取不同视差值的最小代价值。

4 视差精化

经过匹配代价和代价聚合获得精度较高的视差图之后，采用左右一致性检测[17]，对遮挡点进行处理，进一步提高视差图精度。具体方法为：对左图中像素点p，令代价聚合计算后的最优视差为d1，其右图中对应像素点p-d1的视差记为d2，如果|d1-d2|>δ，δ为阈值，则标记像素点p为挡点。对于遮挡像素点p，分别在其左右找到第一个非遮挡点pl和pr，将pl和pr中视差较小的值赋予遮挡像素点p，即d(p)=min{d(pl),d(pr)}。

5 实验结果与分析

实验平台为配置Linux系统的台式电脑，内存搭配2个12G的GPU和1个24G的CPU。在Middlebury数据集进行了实验与结果分析。对比方法采用引言部分所介绍的CNN[12]、NLF[6-7]和以及SGBM算法[8]。

5.1 评价指标

由于文献[12]和文献[6-8]均使用误匹配率和算法运行时间对算法性能进行评价，本文与对比算法保持一致，采用算法误匹配率和算法运行时间作为评价指标。分别在光照变化大、纹理较弱区域、深度不连续区域和全部区域，计算生成视差图中像素点的误匹配率。

误匹配率反映了立体匹配算法的准确度，误匹配率越小说明该区域的匹配精度越高，误匹配率的定义如式(6)所示：

(6)

式中，N表示图像像素点的总个数；P表示所有像素点的集合；Dz表示图像的真实视差，D表示本文计算得到的视差；其中，阈值θ≥1。

5.2 实验数据集与分析

选用Middlebury数据集[18]进行测试实验。Middlebury数据集包括Venus、Tsukuba、Cones和Teddy四组标准立体匹配测试图像对，四幅图像都具有部分光照变化明显、纹理较弱以及深度不连续的特点。四幅测试图像实验结果的视差图如图5所示。

图5 4种算法实验结果生成的视差图

3种对比算法与本文算法在四幅标准测试图像中的误匹配率和运行时间如表1～4所示。

表1 Venus图像中的实验结果

表2 Tsukuba图像中的实验结果

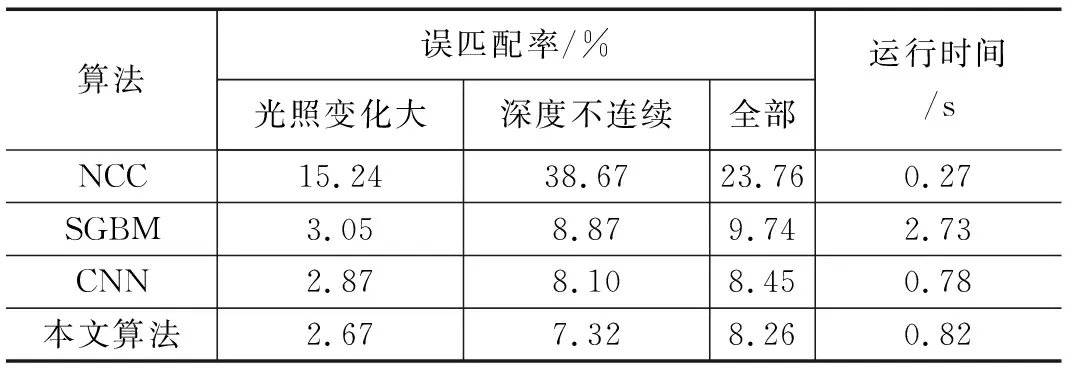
表3 Cones图像中的实验结果

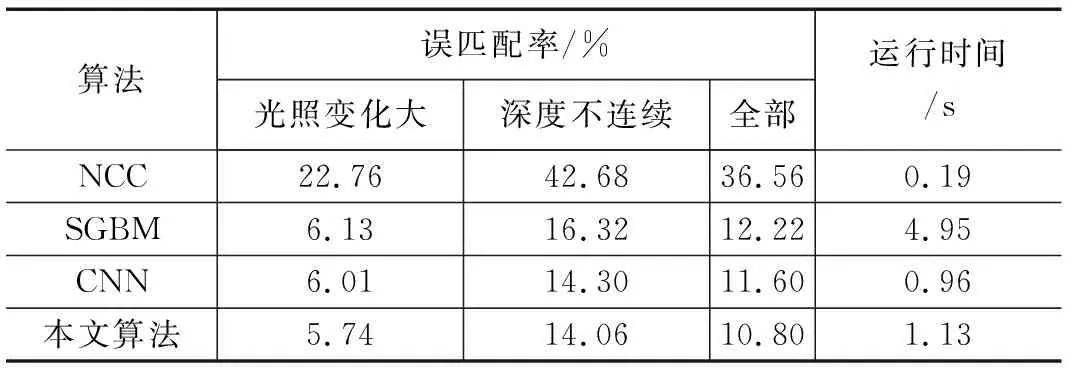
表4 Teddy图像中的实验结果

4种算法的平均误匹配率和运行时间如表5所示。

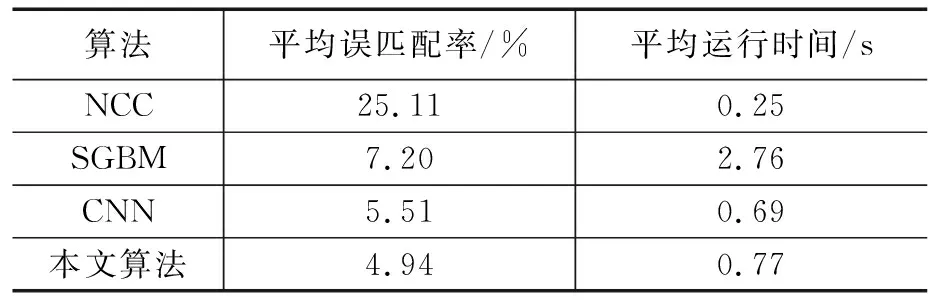
表5 4种算法的平均误匹配率和运行时间

由实验结果表明，在Middlebury数据集中，本文提出的算法相比NLF算法误匹配率降低了10.3%，相比SGBM算法降低了31.4%，在光照变化明显和障碍物边界等深度不连续区域的视差图精度也高于对比算法中的视差图的精度，提高了移动机器人在复杂场景中对障碍物识别的准确度，有利于对障碍物的精准定位。同时，为了全面验证本文算法性能，对算法运行时间进行比较。相比NCC和SGBM算法，本文显著的缩短了算法运行时间，使移动机器人在障碍物检测的过程中具有较高的实时性。由于本文属于半全局立体匹配算法，所以时间相比文献中的CNN算法较长，但也仅为毫秒级别的影响。

同时，为了验证本文算法的实用性，利用双目相机对障碍物进行实拍测试，获取了精度较高的视差图，如图6所示。

图6 自建数据的实验结果

通过立体匹配得到的视差图像中包含了物体在实际空间中的深度信息，为便于观察，利用自建数据实验得到的视差图生成了障碍物的三维点云，如图7所示。

图7 视差图的三维点云图像

从障碍物重建结果可以看出，由于视差图中障碍物边界区域精度较高，所以生成的点云图像中障碍物轮廓清晰，实现了移动机器人对障碍物的精确定位，验证了本文算法的实用性。

综上，本文算法有效地提高了立体匹配算法的视差图精度，在障碍物边界区域(深度不连续区域)和复杂区域的提升较为明显。在建筑工地这类环境复杂，静态障碍物较多的场合，提高了对目标障碍物深度信息获取的精确度，对复杂场景中障碍物三维重建及定位等工作具有重要的意义。

6 结束语

本文提出一种基于多尺度卷积神经网络的立体匹配计算方法，首先，利用多尺度卷积神经网络模型对图像的匹配代价进行初步计算，为提高模型的收敛速度以及稳定性，提出了一种新的损失函数；其次，在代价聚合阶段建立一个全局能量函数，利用动态规划的思想求解最优视差；最后，利用左右一致性检测对所得视差图上的遮挡点进行更正，进一步提高视差图的精度。实验使用Middlebury数据集中的标准立体匹配标准图像对测试算法性能，所有图像对均包含环境复杂光照变化大和纹理较弱区域，实验证明本文算法在光照变化明显、深度不连续以及纹理较弱等复杂环境下所获视差图精度更高，验证了该方法的有效性，并且算法运行速度较快，满足实时性要求。综上，本文算法提高了障碍物检测中立体匹配的精度和效率，在一定程度上提高了移动机器人对障碍物识别的准确度。但是真实的应用场景往往还有更加恶劣的环境以及动态的障碍物需要考虑，这也是后续需要研究的重点。