基于仿真体系模态下的流固耦合场泵站出水塔动力响应特征分析研究

曹 洋，王 逸，邵雨辰

(1.南京市水利规划设计院股份有限公司，江苏 南京 210000；2. 南京市高淳区水务局固城水务站，江苏 南京 211300)

作为重要蓄水调水的水工结构设施，泵站是地区水资源重要调控设备，而其引水调水的重要结构即是出水塔，当出水塔处于蓄水状态时，其结构实质处于流固耦合作用下，而水工结构动力响应特征关乎工程安全运营，因而，研究泵站出水塔等水工建筑地震荷载下动力响应特征很有必要[1- 3]。已有一些学者通过研究构建了水工结构原型，结合振动台试验，获得其动力响应特征试验数据[4- 6]。国内外也有一些学者根据不同地基计算边界模型，开展地震动对岩土层应力变形影响特征[7- 9]。另有一些学者研究了流固耦合下模型计算理论，多采用附加质量或直接流固体作用力耦合[10]，获得了不同计算方法结构多场耦合下模态特征。文章将引入多相耦合分析理论，并对比不同地基边界条件仿真模型[11- 12]，计算地震荷载下泵站出水塔动力响应特征，为泵站安全运营评判提供理论参考。

1 多相耦合理论

水工结构常常处于多相场作用下，其结构的动力响应特征受到多场耦合影响，故而在仿真计算时引入附加质量法理论，为多相耦合下泵站出水塔动力响应求解提供依据。附加质量法原理主要是指水流动压力转化为施加在固体结构上的质量力，根据水流状态，施加作用点产生差异性，进而求解结构动力响应特征。其中，结构运动服从以下方程：

(1)

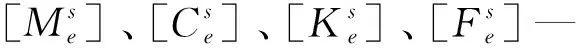
耦合水流介质后，振动方程为

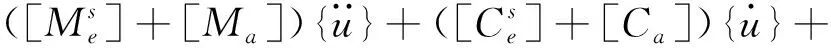
(2)

式中，[Ma]、[Ca]、[Ka]—流体自有属性特征参数的矩阵，包括质量以及刚度等。

假定流体介质运动为理想状态，即无刚度运动，则式(2)可简化为

(3)

由于文章研究对象为泵站出水塔，因而将蓄水池与压力管道中水流介质作为附加质量，其计算公式如下：

(4)

式中，η—转换系数；β、H—流体所在流场宽度与深度；Z—计算深度；ρ—密度值；M0—附加质量参数。

文章所研究的动力外荷载以地震动作为外参数，故而应考虑地震动输入仿真体系中，将地震动荷载等各特征参数以等效变环手段，作用到仿真体系节点上，即以等效节点应力为基准，其表达式如下：

(5)

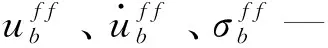
地震荷载对固体结构的作用实质上是由地震波进行传递能量至结构节点，因而，根据地震波作用在地基上位移变化表征了地震动荷载强度，其应变表达式为

(6)

(7)

结合应力-应变之间比例关系，以地震波各方向传递速度为求解量，获得任意节点处在某一时刻的位移与加速度为

(8)

(9)

式中，D—作用点到边界的距离；d—黏弹性模型中边界点与作用点之间距离；Cs、Cp—特征参数向量式。

对由等效节点荷载组成的矩阵元素值进行外荷载施加，即可表示地震动荷载作用。

2 工程概况

江苏北部灌区为提升水资源高效利用，建有一项引水工程，该引水工程为一泵站群，以梯度调度为原则，主要面向地区内生活用水以及农业灌溉，灌溉农田超过300km2，可提供100万m3的生活用水，设置超过200台泵机，可运行负荷超过12万kW。其中，禾家镇泵站建设规划蓄水池、出水塔及其他附属水工设施，按照正常运营符合85%供水，建有一条贯穿全灌区的干渠，长度约为24.6km，可满足不同作物灌溉需水要求，所有输水渠道设施均设置为混凝土衬砌结构形式，以降低渠道输水损耗，禾家镇泵站设计供水渠道流量为50m3/s，在调压池内通过弧形钢闸门输送水资源至渠首，各水工结构设施均以混凝土浇筑形成，以保证泵站整体结构稳定性。出水塔顶部高程为1598.79m，表层设置砂浆抹灰面的毛石挡墙，降低水流渗流活动性，保证泵站在枯水季运营期间，可由出水塔每天供应1.5万m3的水量至涵管内，向城区与农村输送生活用水。泵站出水塔包括塔身、塔基及混凝土塔顶，蓄水池建设在塔顶上，以厚度为0.3m的混凝土浇筑形成，渡槽顶面设置在池底部，渡槽排架高度最大为17m，输水涵管以钢架梁及0.25m厚的隔板支座安装在蓄水池底部，另外，为保证蓄水时塔身安全稳定，有2根混凝土圆形柱作为加固结构，其间距为2m，出水塔主体承重结构几何示意图如图1所示。

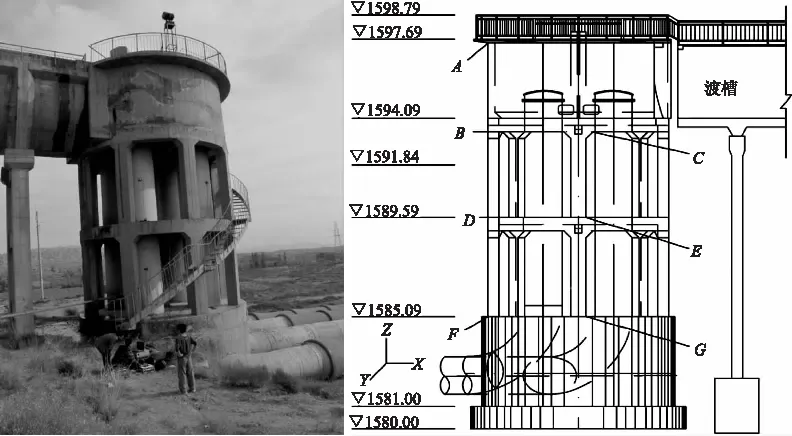
图1 泵站出水塔实图与几何示意图(单位：m)

泵站所在工程场地位于淮河支流下游冲击平原上，距离泵站15km处为丘陵地形，是整个场地内最高点，区域年降雨量监测值为850mm，场地表面覆盖土层为第四系堆积土层及河漫滩沉积土，以细砂土为主，厚度约为2.4～4.6m，下卧土层中还含有粉质壤土，含水量较低，现场取出的试样表明其颗粒处于较干燥状态，但承载力较高，灌区内干渠基础即以该土层为持力层，壤土颗粒比细砂土要粗，颗粒粒径约为2.6～5.8mm。在壤土以下基岩层中以强风化片麻岩为主，完整性偏差，取出的样品表明片麻岩局部夹有破碎带，含有泥质等砂岩，分析是由于河流内泥沙长期堆积形成，并侵入片麻岩破碎带内，一定程度上影响了片麻岩的完整性。根据水文地质资料得知，河流内含沙量较高，主要是由于岸坡上黄沙与淤泥质土稳定性差，卷入河流中，并逐渐在下游淤积。另一方面，由于泵站在设计之初未设计隔震支座等抗震结构设施，而出水塔作为重要水工结构，在地震动力下其安全稳定性将关乎泵站的安全运营。

3 动力响应特征分析

3.1 出水塔仿真模型体系

在上述理论与工程资料分析基础上，文章将借助有限元数值软件建立泵站出水塔仿真模型体系，以输水渠道流向为X向、出水塔涵管方向为Y向，竖向轴为Z向，按照出水塔尺寸及场地岩土材料，以SOLID65模型作为单元体，场地岩土地基以SOLID45作为离散单元，共划分单元网格43342个，节点数32652个，所建立的仿真模型如图2所示，另在地基表面采用黏弹性体系处理自由度，包括出水塔的压力涵管与近地表结构等，均为结构-水流-地基的三相场耦合边界条件，其边界仿真模型如图3所示。

图2 泵站出水塔仿真模型图

图3 黏弹性地基边界仿真模型

3.2 自振特性分析

泵站出水塔自振特性与地震荷载下共振现象有关，研究不同工况下出水塔的自振频率，为抗震设计提供重要理论参数。仿真体系以附加质量法建立流固耦合模态分析框架，特别地为比较水流对出水塔自振特性影响，建立有、无水流的两种研究工况，获得两种模型多阶态下振型云图及自振频率，如图4、图5所示。

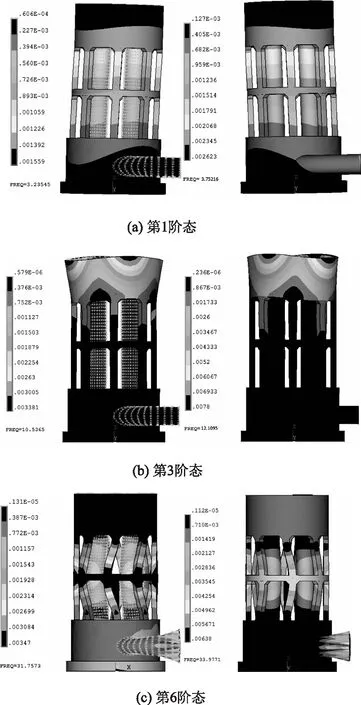
图4 泵站出水塔振型云图(左、右分别为有、无水工况)

从图4可看出，当出水塔处于流固耦合时，振型云图显示在各阶态计算下，均是塔顶处频率强度值处于低水平，同一计算阶态下塔身处各承重柱频率分布基本一致，印证了前文所述蓄水池下防承重混凝土柱具有一致性变形特性。对比无水流工况下，有水流工况的同一结构部位处的频率强度值低于前者，第1阶态下无水流工况下频率强度值为0.002623，而有水流工况下的频率强度值相比降低了40.6%，即水流运动会在一定程度上削弱出水塔频率分布强度值。同一计算阶态下，出水塔有、无水流工况的振型分布云图具有相似之处，不论是在塔顶亦或是在塔基处，仅在分布频率强度量值上会有一定差异，如第1阶态下有、无水流工况的振型分布均为X向振型，而第3、第6阶态下均为对称性振型分布。

图5为有、无水流两种工况下计算所获得的自振频率值，从有水工况下自振频率变化曲线可看出，随着计算阶态的增大，自振频率值逐渐升高，第6阶态下的自振频率为31.76，相比第1阶态下增大了8.7倍；无水流工况下，计算阶态与自振频率亦呈正相关，其中第6阶态相比第1阶态增大了8.2倍，两个工况下的增长幅度基本相近。对比两个工况下同一阶态下自振频率可知，无水工况下自振频率不论在任何一个计算阶态下均高于有水工况，有水工况下第1阶态自振频率为3.24，第1阶态下无水工况比有水工况高16.2%，而在第3阶态下幅度仍然维持在接近15%，但第6阶态下两者差距变为7%，即有、无水流工况间自振频率差异随着计算阶态的增大而逐渐降低。综上分析，在低阶计算阶态中，泵站出水塔自振频率受水流作用影响较大，高阶计算阶态中两者差距逐渐缩小。

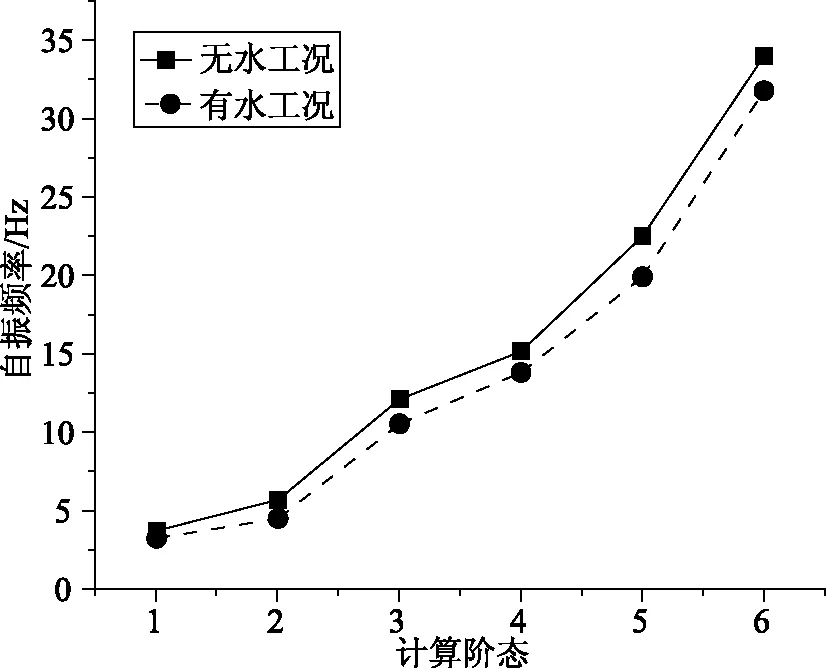
图5 自振频率变化曲线

3.3 地震响应分析

地震荷载输入选取连云港地区某条监测地震波作为地震动输入数据，峰值加速度以0.2g作为输入计算，根据傅立叶滤波方法，获得输入动荷载的时程曲线，如图6所示。文章将在地震动荷载输入下分析泵站出水塔位移与应力响应特征，并设定蓄水池有、无水流工况，结合两种荷载传递边界模型：黏弹性边界模型与零质量地基模型，故共有四种研究工况。由于出水塔模型节点较多，笔者以出水塔顶部蓄水池边缘外侧特征点A的位移与应力开展分析。

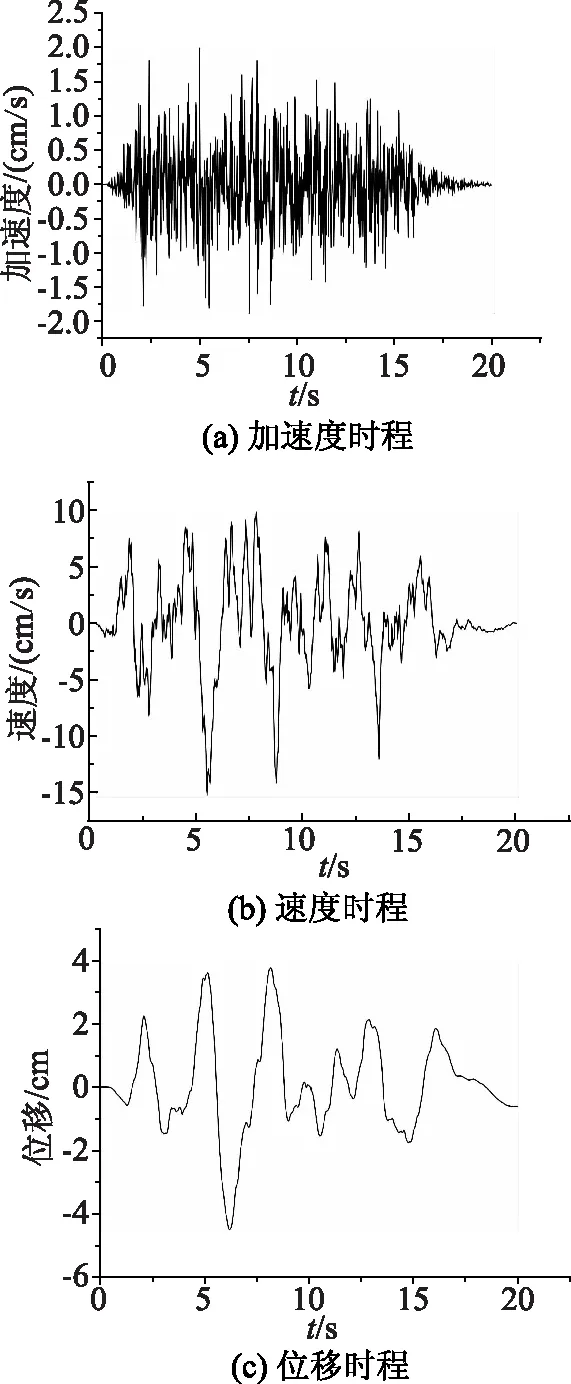
图6 地震动荷载时程曲线

3.3.1位移响应

计算获得不同工况下各向位移时程曲线，限于篇幅，文章仅给出四种工况下特征点A在正、负方向上最大位移值，如图7所示。从图7中可看出，零质量地基模型下X正向最大位移值为有水工况下，达6.82mm，无水工况下最大X正向位移仅是它的48.5%，X负向位移亦是如此；Y向位移中，无水工况下正向、负向位移均低于有水工况，即水流耦合固体作用下对其水平与纵向位移均有较高程度的影响。黏弹性地基边界模型计算出的位移结果亦是有水工况下的位移值高于无水工况，最大相差达3倍。分析表明，水流作用下会增加结构在地震荷载作用下惯性力，造成其位移响应更大。对比同一计算模型下各向位移特征可知，同一工况下X、Y向位移总高于Z向位移，即水平横向刚度相比竖向要低，零质量地基模型中无水工况下Z正向位移为0.7mm，而X、Y向位移相比前者均一致高了4.7倍，因而该出水塔设计时应特别考虑水平横向抗震能力。对比两种地基模型计算结果可看出，同一工况下零质量地基模型计算出的位移值高于黏弹性边界地基模型，前者在有水工况下Y正向最大位移值相比后者高了57.8%，表明黏弹性边界地基模型考虑地基阻尼系数远域减小特征效应，降低了泵站出水塔动力响应效应。

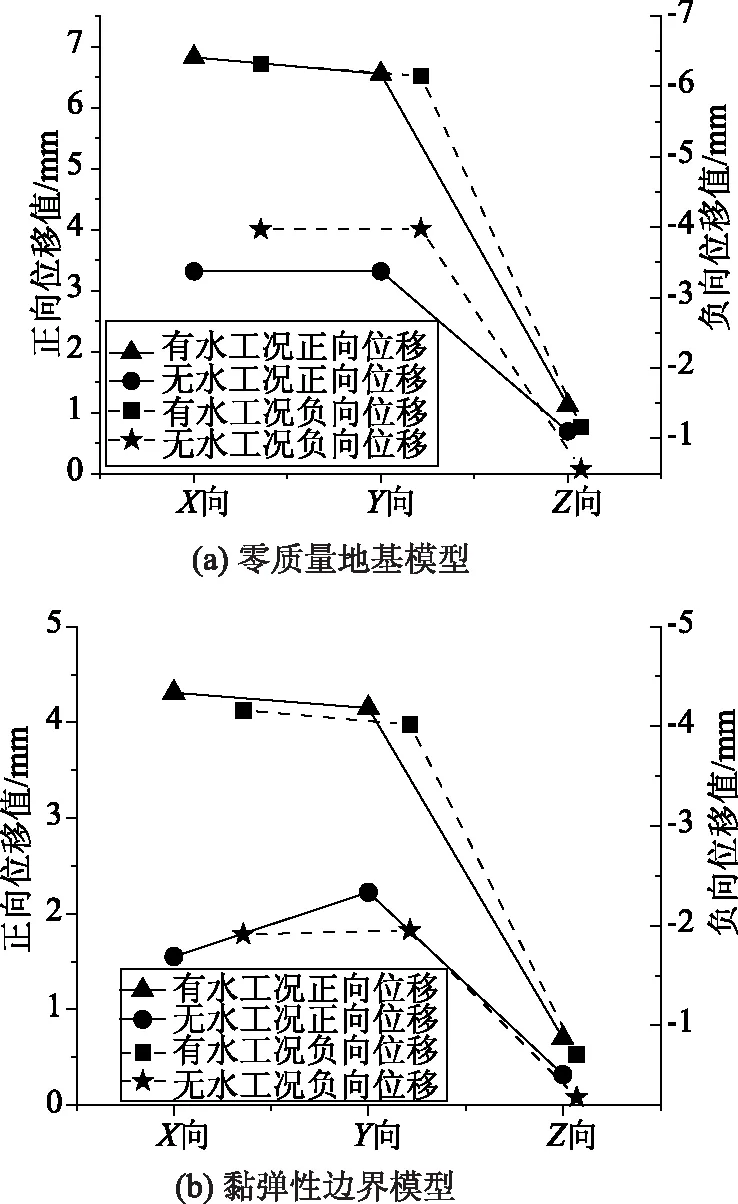
图7 各方向上位移峰值变化曲线

3.3.2应力响应

图8为特征点A分别在有、无水流工况下的第一、第三主应力分布云图。由此可看出，不论是第一主应力亦或是第三主应力，有、无水流工况下的应力响应分布具有一致性，即应力分布形态相似或一致，但差异点出现在第一、第三主应力量值上，第一主应力中在有水工况下的最大值为1.27MPa，而在无水工况下同位置的最大第一主应力相比前者降低了57.8%；各应力峰值均位于蓄水池支撑排架与下方墩座交界面处，抗震设计时应考虑重点加固该区域刚度。

图8 出水塔应力分布云图

选取泵站出水塔模型自上而下特征节点B～G，分别给出不同工况下第一、第三主应力峰值曲线，如图9所示。从图9中可看出，在有水工况下，零质量地基模型计算所获得的第一、第三主应力均高于黏弹性边界模型。特征点C在黏弹性边界模型中计算所获得的第一主应力峰值为0.604MPa，而该点在零质量地基模型中的计算值相比增大了54.3%，达0.932MPa，这与前文位移响应特征中黏弹性模型考虑阻尼系数远域效应一致。对比同一地基边界模型条件下，无水工况下应力参数值均低于有水工况，流固耦合下第一、第三主应力地震响应水平显著提高，黏弹性模型中特征点D在有水工况下的第三主应力为0.882MPa，而无水工况下在相同模型中其值相比减少了57%，为0.379MPa。从各特征点的应力峰值来看，零质量地基模型在有水工况下第一主应力峰值点为G点，达1.93MPa，第三主应力亦为该点，达2.1MPa；无水工况下第一、第三主应力峰值分别为1.34、1.04MPa,,均处于材料强度允许安全值合理区间内，即泵站出水塔应力响应符合规范要求[13]。

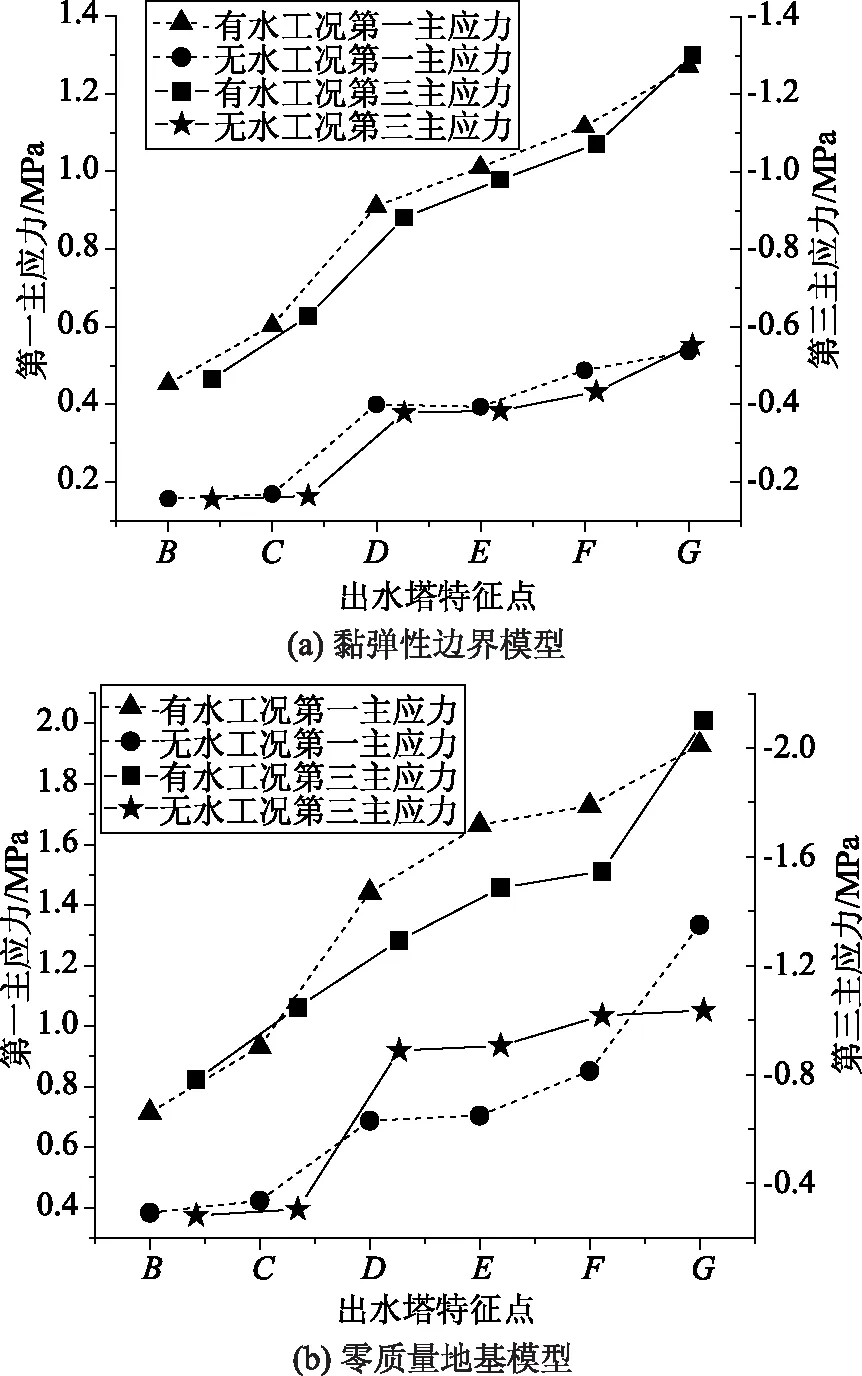
图9 第一、第三主应力峰值变化曲线

4 结论

(1)出水塔在有、无水工况下自振振型分布一致，但有水工况振型强度低于无水工况；计算阶态与自振频率呈正相关，无水工况下的自振频率高于有水工况，但差距随着计算阶态增加而降低。

(2)地震荷载下出水塔无水工况下正、负向位移均低于有水工况；X、Y向位移均高于Z向；零质量地基模型计算出的位移值高于黏弹性边界模型，有水工况中两者Y正向最大位移相差57.8%。

(3)地震荷载下出水塔在有、无水工况下的主应力分布一致，但在量值上无水工况低于有水工况，危险断面均位于排架与墩座交界面；零质量地基模型计算出的应力值高于黏弹性边界模型。