一种实用的飞行器捷联惯性导航算法

陈柯勋，邱 伟

（1.太原理工大学 信息与计算机学院，太原030600；2.北京强度环境研究所，北京100076）

随着我国航天事业的蓬勃发展，飞行器定位导航的精度和效率不断提升。其中，捷联式惯性导航系统由于成本低、便于安装、无需天线等特点，常用于小型飞行器导航系统中。捷联式惯性导航系统是把惯性敏感装置直接安装在飞行器上来获取飞行器的初始姿态信息、初始速度信息和初始位置信息，然后通过捷联惯性导航解算算法确定飞行器方位、速度和位置的自主式解算导航系统［1］。

捷联惯性导航系统的效率和可靠性取决于捷联惯性导航解算算法，目前已有较多学者在该领域取得了较多的研究成果。例如，尹剑等［2］开展了捷联惯导飞行器旋转矢量姿态优化相关的研究，通过对旋转矢量的姿态算法进行优化来提高姿态计算的精度；陈凯等［3］针对临近空间飞行高度，研究了发射惯性坐标系和当地水平坐标系下惯性导航解算算法的等价性；温永智等［4］则提出了卫星载波相位与捷联惯导组合方法对高轨机动飞行器进行自主导航。总体来看，针对飞行器捷联惯性导航系统解算算法，国内外的研究成果大多是针对基础理论，没有给出一种实用性较强的解算算法以及相应的惯性系统安装与实现方案［1-8］。

因此，本文提出了一种可实现的捷联惯性导航解算算法，并在试验过程中通过安装示意图描述了惯性系统在飞行器中的安装与实现方法。本文所述算法的有效性和可靠性经过了实际试验验证，具有一定的理论意义和现实意义。

1 捷联惯导解算算法

1.1 算法原理

捷联式惯性导航系统是把惯性敏感装置（陀螺仪和加速度计）直接安装在运载体上，利用惯性敏感装置、初始姿态信息（偏航角、俯仰角和横滚角）、初始速度信息（东向速度、北向速度和垂向速度）和初始位置信息（地理经纬度）确定载体方位、速度和位置的自主式解算导航系统。捷联惯性导航解算是将惯性敏感装置的信息从载体坐标系转换到导航坐标系（地理坐标系）的计算过程，现对这两个坐标系作介绍［9-10］。

1.1.1 导航坐标系（OXnYnZn）

导航坐标系如下：以地球表面为XOY平面，以本初子午线与赤道交点（即经纬度均为0的点）为坐标原点O，沿纬线方向定义X轴（向东为正），X坐标范围为（-180，180）；沿经线方向定义Y轴（向北为正），Y坐标范围为（-90，90）；Z轴垂直XOY平面，向上为正，构成右手坐标系，通常也叫做东北天坐标系。对于导航坐标系，坐标轴还有不同的取法，如北西天、北东地坐标系。在此坐标系下，地球表面点的Z坐标均为0，而X和Y坐标分别以经度值L和纬度值B来表示。

1.1.2 载体坐标系（OXbYbZb）

载体坐标系与飞行器本体固联，并同飞行器一起运动（包括移动和转动）。坐标系的原点O取飞行器的质心，OXb轴沿飞行器的横轴指向右，OYb轴沿飞行器的纵轴指向前，OZb轴垂直于OXb轴指向上方。三个坐标轴构成右手正交直角坐标系。载体坐标系相对惯性坐标系的方位为飞行器的姿态。飞行器的姿态定义如下。

航向角：预定的航行方向为航向，在水平面内，用北向基准线与航行线之间的夹角表示航向角，以北向基准为0度角，顺时针为正，逆时针为负。定义域为［0，360）度。

俯仰角：飞行器纵轴与水平面之间的夹角为俯仰角，向上为正，向下为负，定义域为［-90，90］度。

横滚角：飞行器纵轴与水平面之间的夹角为俯仰角，右倾为正，左倾为负，定义域为［-180，180］度。

1.2 算法总体设计

本文所设计的捷联惯性导航解算算法如图1所示。

图1 捷联惯导解算算法原理框图Fig.1 Block diagram of strapdown inertial navigation algorithm

根据图1所示原理，捷联惯导解算算法流程通过以下步骤实现：

1）确定导航坐标系。包括载体坐标系和导航坐标系的建立，沿着飞行器前进方向，载体系OXbYbZb对应右-前-上坐标系方向，导航坐标系OXnYnZn采用东-北-天坐标系［5］。

2）确定初始状态，根据初始姿态计算出初始位置矩阵Cnb.初始状态作为捷联解算的时间起始点，包括飞行器的姿态信息（航向角、俯仰角和滚动角）、速度信息（东向、北向和垂向速度）、位置信息（飞行器的经纬度）。

3）将初始姿态信息用四元数法构造初始姿态矩阵（捷联矩阵），用初始经纬度信息构造初始位置矩阵。

4）由初始时刻T的捷联矩阵、陀螺输出角速率信息及初始位置速度信息计算，同时根据位置信息计算，根据地球自转速率计算ωnie，进而根据捷联矩阵更新公式下一个采样点T＋1时刻的捷联矩阵，最终根据四元数的运动学微分方程从而计算出飞行器在该时刻的姿态角和位置［6］。

5）根据（4）得到的捷联矩阵和加速度及输出加速度信息解算出飞行器该时刻在东北天三个方向的加速度分量。

6）重复步骤（3）至步骤（5），直到采样数据解算结束。

7）最后得到每个采样时刻的姿态矩阵、位置矩阵、速度矩阵从而计算出姿态、位置和速度信息。

按照以上步骤重复进行就可以对捷联惯导数据进行解算。其中，采用四元数法进行姿态计算，用毕卡近似法求解微分方程。上面解算过程，共使用了三个基本计算过程，即姿态更新、速度更新、位置更新。

1.3 姿态更新

记载体系OXbYbZb为b系，记“东-北-天（E-NU）”地理坐标系（n系）作为捷联惯导系统的导航参考坐标系，则以n系作为参考系的姿态微分方程为：

式中：ωnin表示导航系相对于惯性系的旋转，它包含地球自转引起的导航系旋转，以及系统在地球表面附近移动因地球表面弯曲引起的导航系旋转，即有

根据矩阵链乘规则，有：

式中：角标括号中的符号m表示tm时刻。由于i系是绝对不动的惯性参考坐标系，它与时间无关，不需标注时刻；而n系和b系相对于i系都是动坐标系，均跟时间有关，需标注时刻。

将式（6）和（7）代入式（5），得：

通常在导航更新周期［tm-1，tm］内，可以认为由速度和位置引起的变化很小，即可视为常值，记为，则有：

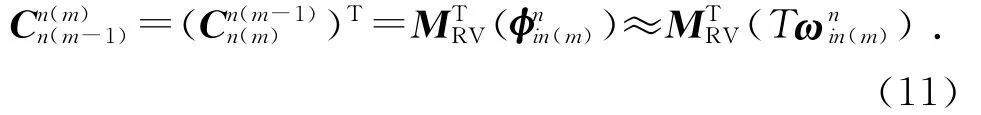
式（8）～（11）即为捷联惯导数值递推姿态更新算法。

在实际工程应用中，首先需要根据惯性敏感装置给出的初始姿态角，依据初始姿态角求取四元数：

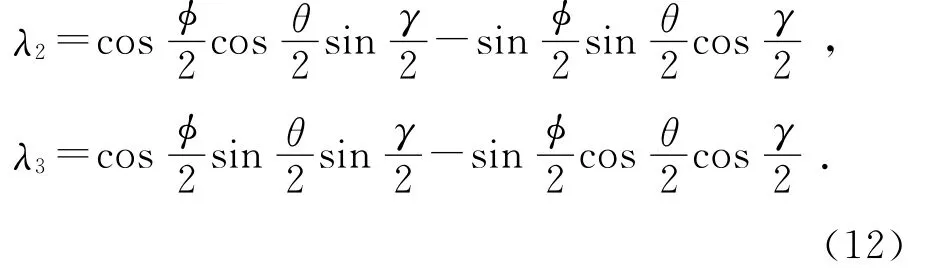
式中：θ，γ，φ分别为俯仰角、横滚角和偏航角。

进而根据四元数求方向余弦矩阵：

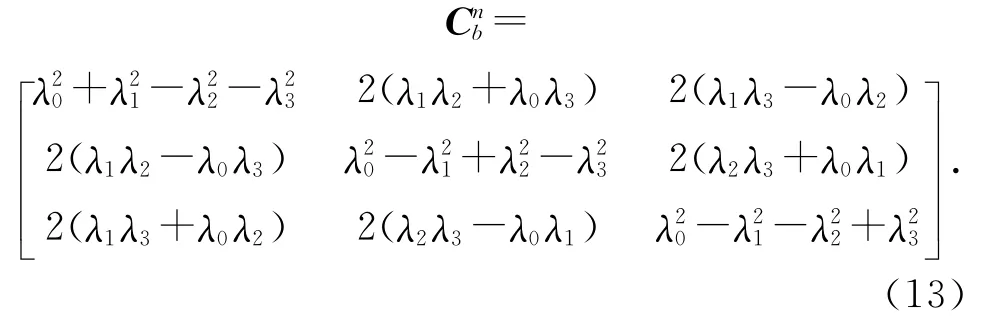
姿态角与姿态矩阵的关系：

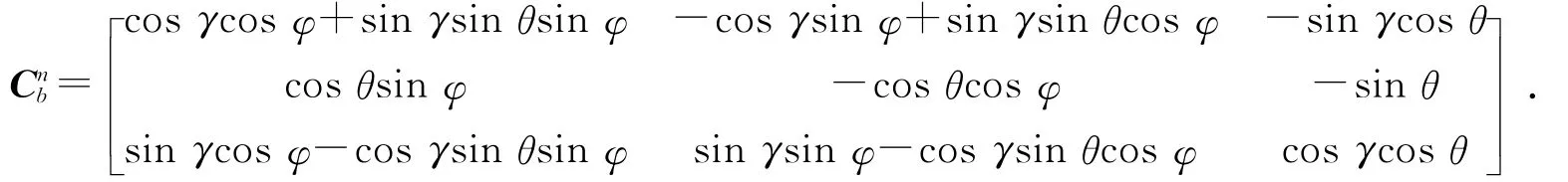
式中：θ，γ，φ分别为俯仰角，横滚角和偏航角。如果记：

则由以上两式即可解算出姿态角：

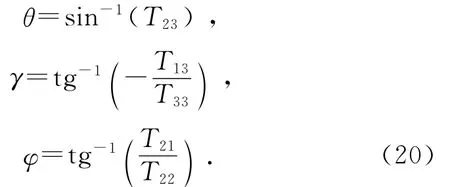
1.4 速度更新

惯导比力方程一般形式如下［10-13］：

在比力方程（21）中将vnen简写为vn，并明确标注出各量时间参数，如下：

上式两边同时在时间段［tm-1，tm］内积分，得：

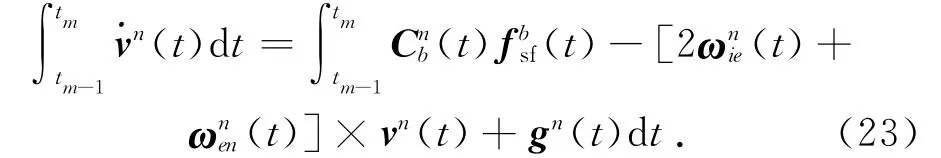
即

将式（24）移项，可改写成递推形式：

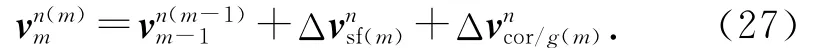
速度更新变为主要讨论 Δvnsf（m）和 Δvncor／g（m）的数值积分算法。实际工程应用解算中，地理坐标系相对地球坐标系的角速度为：

加速度计获得的比力信息fibb为载体坐标系中各个轴向的比力，而我们需要的比力finn为地理坐标系中各个轴向的比力，它们之间应用矩阵Cnb做变换：

根据比力信息可以求出各个方向上的加速度：

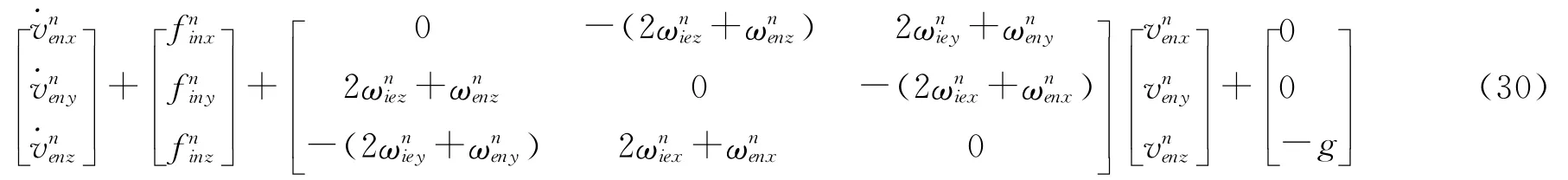
因此可以求得速度为：

1.5 位置更新

捷联惯导系统的位置（纬度、经度和高度）微分方程式可以表示如下：

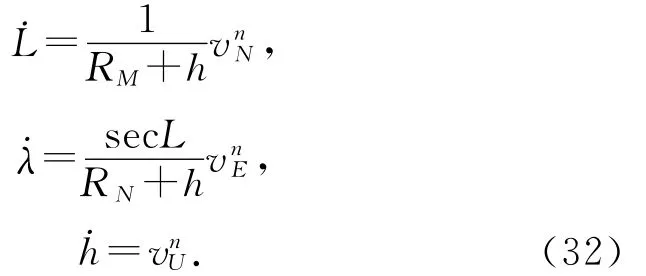
将它们改写成矩阵形式，为

其中，记：

与捷联惯导姿态和速度更新算法相比，位置更新算法引起的误差一般比较小，可采用比较简单的梯形积分法对式（33）离散化，得：

上式移项，便得位置更新算法：

其中，Mpv（m-1／2）可 采 用 所 示 的 线 性 外 推 算 法［13-16］。

可对矩阵整体Mpv进行外推，亦可对矩阵元素中的位置变量L，h外推，再构造矩阵Mpv.

实际工程应用中，载体所在位置的地理纬度L、经度λ可由下列方程求得：

其中，Rxt＝Re·（1＋esin2φ）为地球参考椭球 WGS-84的子午圈曲率半径，Ryt＝Re·（1-2e＋3esin2φ）为相应的卯酉圈曲率半径，e＝1／298.257为相应的椭圆度。

2 捷联惯导算法应用实例

本文通过试验水箱模拟飞行器，通过试验水箱空投试验来对本文所述算法的有效性进行验证。

2.1 试验条件

试验前，为了保证测量前端的准确性，选择了进口的陀螺仪和加速度计。陀螺仪选用了美国NXP公司的FXAS21002C三轴陀螺仪，具体指标如下：

1）采用紧凑型QFN封装；

2）2.7mA工作电流（2.8μA待机电流）；

3）角速率分辨率为0.062 5dps／LSB；

4）动态可选的全量程范围（±250／±500／±1 000／±2 000°／s）；

5）32采样FIFO；

6）输出数据频率（ODR）范围：12.5～800Hz；

7）工作温度范围：-40～＋85℃.

加速度计选用了美国Endevco 2230E型三轴向压电式加速度计，具体指标如下。

1）灵敏度：3pC／g；

2）正弦振动极限：1 000g；

3）冲击极限：2 000g；

4）频率响应：1～10 000Hz；

5）温度范围：-55～＋260℃；

6）质量：17g.

试验过程中，将空投数据记录装置安装在水箱内部的凹槽内，惯性测量单元及气压高度计固定在水箱上盖板内侧，具体安装位置及方向如图2所示。

图2 数据记录装置、惯性测量单元及气压高度计安装示意图Fig.2 Installation diagram of data recording device，inertial measurement unit and barometric altimeter

试验水箱在机舱内的安装如图3所示。

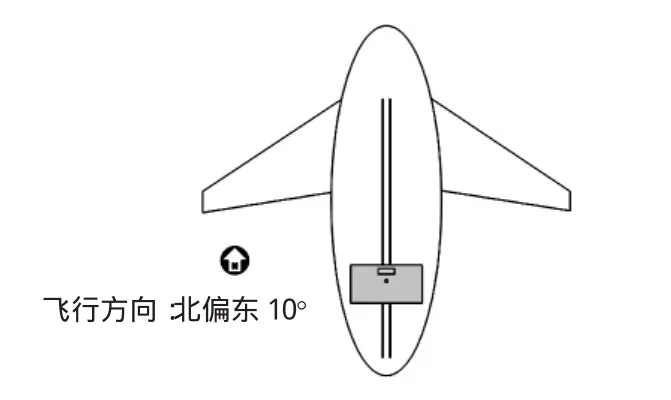
图3 试验水箱在机舱内的安装示意图Fig.3 Installation diagram of test water tank in engine room

飞机在落区投放时，试验水箱从飞机尾部的滑轨投下，投放时刻的参数如表1所示。

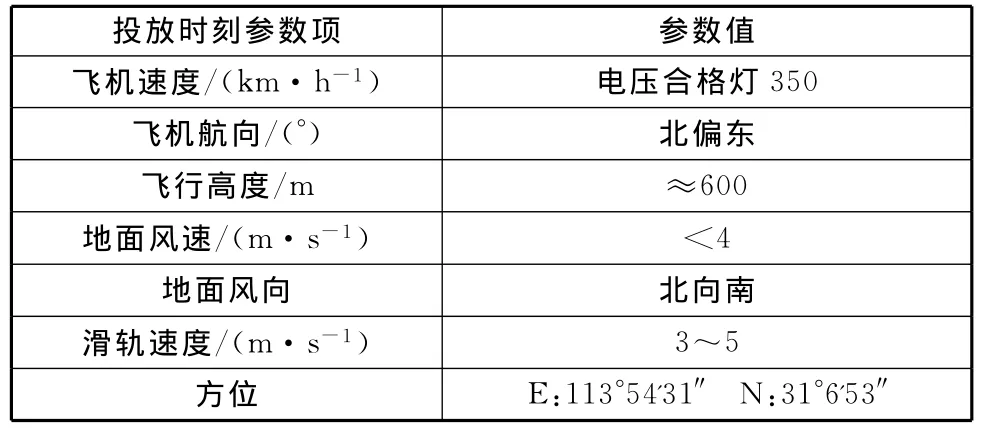
表1 空投试验参数表Table 1 Airdrop test parameter table

试验水箱落点的参数：方位 E：113°54＇41″，N：31°7＇38.4″，纬度为31°时的每秒约合26.4m，经度的每秒约合31m.

2.2 试验结果分析

根据试验水箱中的数据记录装置导出的数据，可以得出陀螺仪输出角速度时域波形如图4所示。

加速度计过载时域波形如图5所示。

通常情况下，捷联惯导解算算法的运算结果与多种因素有关，其中就包括陀螺仪和加速度计的精度和误差模型，但从图4和图5中可以看出，空投试验所选用的陀螺仪和加速度计精度较高，测量数据没有影响捷联惯性导航解算算法的解算过程，因此可以不考虑该项因素的影响。

图4 陀螺仪输出角速度时域波形图Fig.4 Waveform of gyroscope output angular velocity

图5 加速度计输出加速度时域波形图Fig.5 Waveform of accelerometer output acceleration

使用本文所述算法对试验水箱中采集到的试验数据进行解算，可以得到飞行器的三个姿态角变化曲线如图6所示，飞行器的三向位置变化曲线如图7所示。

图6 本文算法解算后飞行器姿态变化曲线图Fig.6 Attitude change curve of aircraft after the algorithm

从图6和图7可以看出，本文所述算法解算出来的姿态、位置结果与实际落地点的姿态和位置信息吻合。综合分析整个试验结果，可以证明本文所述算法的有效性和可靠性。

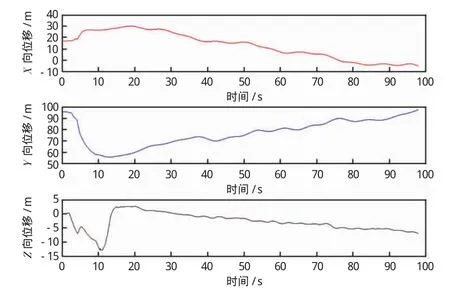
图7 本文算法解算后飞行器位置变化曲线图Fig.7 Position change curve of aircraft after the algorithm

3 结论

本文所提出的捷联惯性导航解算算法借助四元数法进行飞行器姿态和位置信息解算，算法运行过程简洁高效，可实施性强，试验设计切合实际应用场景，可以为相关领域提供参考，具有一定的理论意义和实用价值。