基于局部线性嵌入的行星变速箱测点优化研究
2020-09-24王子涵冯辅周
王子涵,冯辅周
(陆军装甲兵学院车辆工程系,北京 100071)
0 引言
某型行星变速箱作为主战坦克传动系统的重要组成部分,具有传动比大、体积小、重量轻等优点。变速箱工作时,由于其载荷较大、结构复杂、换挡频繁,太阳轮、行星轮、轴承等关键传动部位易产生故障[1]。对其开展故障诊断研究能够及时评估行星变速箱运行状态,保障持续战斗水平,避免行星变速箱严重损坏。
在对行星变速箱进行故障诊断技术研究时,由于行星变速箱结构复杂,拆装换件困难,在台架试验前应进行动力学仿真分析,这一前置工作可以为台架试验提供理论依据与思路设计。陈诚基于ADAMS 与ANSYS 构建了两级行星齿轮箱刚柔耦合模型,为行星齿轮系统故障诊断技术研究提供了理论依据[2];郝驰宇建立了汇流行星排的刚柔耦合多体动力学仿真模型,仿真分析了断齿故障下接触力及加速度信号[3];马德福以轴承系统为对象建立刚柔耦合模型,验证了刚柔耦合模型的精度比纯刚体模型更高[4]。
试验采集行星变速箱振动信号时,三级行星传动产生噪声干扰增加了故障特征提取的难度。测点对故障特征的敏感度不同,会影响后续的故障诊断准确率。前期故障诊断工作中[5-6],台架试验往往选取行星变速箱内部测点振动信号提取故障特征,而考虑到无法布置内部测点的试验台以及实车试验,需要对外部测点进行优化选取以提高故障诊断的准确率。
对传感器的测点优化研究已经取得许多有效方法,如模态动能法、奇异值分解、粒子群算法等,在桥梁、模拟电路的状态检测中得到运用,但是需要大量测点的实测数据作为支撑[7],对结构复杂的行星变速箱研究较少,且缺少后续故障诊断准确率的有效验证。
运用无监督学习的局部线性嵌入算法(Local Linear Embedding)对行星变速箱进行外部测点的优化分析,运用ADAMS 对行星变速箱刚柔耦合模型注入故障;初步选取测点,运用局部线性嵌入算法计算测点对故障的敏感度排序,确定台架试验的传感器布置点;对实测振动信号进行时域特征提取,借助BP 神经网络算法进行不同故障状态识别的准确率分析,以验证局部线性嵌入算法进行测点优化的有效性和可靠性。
1 行星变速箱动力学建模
1.1 行星变速箱基本结构
行星变速箱传动部分由三个行星排构成,共有五个前进挡、一个倒挡和一个空档,通过控制不同的摩擦制动器来约束不同部件的运动,实现稳定的动力输出,并在较大的范围内改变传动比。行星变速箱结构如图1 所示。
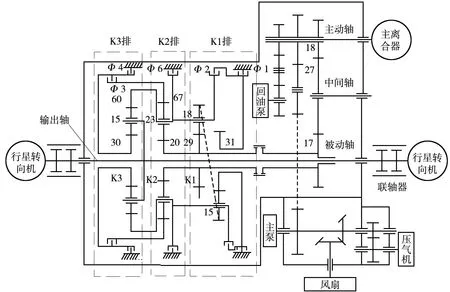
图1 某型行星变速箱结构
1.2 刚柔耦合模型的建立
行星变速箱刚柔耦合模型建立过程如下:
(1)在SolidWorks 软件中建立变速箱各部件的三维模型,并进行装配与干涉检查。
(2)为研究行星变速箱内部振动在箱体表面的响应,将箱体由刚体模型转为柔性体模型。使用ANSYS 软件对模型进行柔性化处理,并生成模态中性文件。网格划分结果如图2 所示。
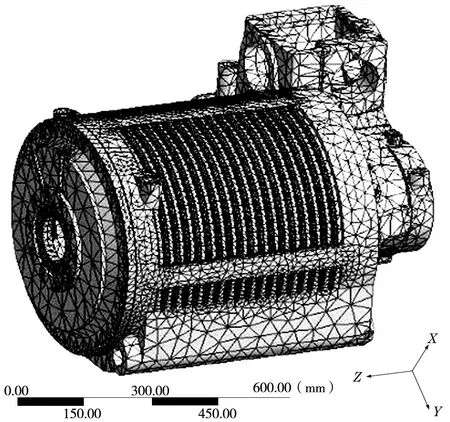
图2 行星变速箱箱体网格划分
(3)将柔性化的箱体模型导入ADAMS 中添加约束与接触,建立行星变速箱刚柔耦合模型。建立的刚柔耦合模型如图3 所示。

图3 行星变速箱刚柔耦合模型
1.3 故障模型的建立
根据文献中的统计分析结果,齿轮失效约占失效部件的60%,是导致变速箱故障的最主要原因[8]。选取K3 排Z30 太阳轮(简单排)与K1 排(复合排)Z31 太阳轮、Z18 行星轮为对象,注入齿轮接触疲劳剥落故障。齿轮故障模拟模型如图4 所示。
行星变速箱的刚柔耦合模型建立后,通过SolidWorks 软件编辑齿轮,导入ADAMS 中替换原有部件以模拟不同的故障状态。

图4 齿轮故障模拟模型
2 测点优化
2.1 局部线性嵌入算法原理
局部线性嵌入算法的优势在于保持局部几何性质不变,并通过重构维度扩展到空间当中[9]。
局部线性嵌入算法原理如下:
(1)对于一个给定的数据集:

在高维空间中依据欧氏距离搜索每个样本点xi的k 个近邻点:

则样本点可用k 近邻的数据点线性组合表示。
(2)计算样本点邻域的重构权值。构建一个局部重建权值矩阵,并使损失函数最小化:

其中,wij=[w1,w2...,wN] 为重构权值矩阵;Xij为Xi的k 个近邻点。
(3)计算最佳重构的低维嵌入向量Y。由于重构权值描述了每个邻域的固有几何属性,而不依赖于特定的参照系,所以由(2)计算的重构权值矩阵依然有效。再次使损失函数最小化:

其中,Yi为Xi在低维空间的映射,Yij是Yi的k 个近邻点。
需要注意的是,重构权值wij反映了数据的固有属性,映射到的局部流形上仍具有原数据的几何结构[10]。
2.2 测点初选与仿真
根据传感器布置的有效性和可行性原则[11],保证传感器便于安装并且尽可能的靠近振源部位,依据箱体的结构特点和模态分析,初步选择了10 个测点,其位置和编号如图5 所示,测点位置说明见表1,其测试方向均为垂直于箱体表面方向。
以正常状态和三种故障状态下的仿真信号为分析对象。其中三种故障状态分别位于K3 排Z30 太阳轮、K1 排Z31 太阳轮、K1 排Z18 行星轮,以尽量减少噪声干扰、增强故障响应为目的,参照各档位行星排的工作情况,选取变速箱档位为档。各档位行星排工作情况见表2。

图5 测点布置图
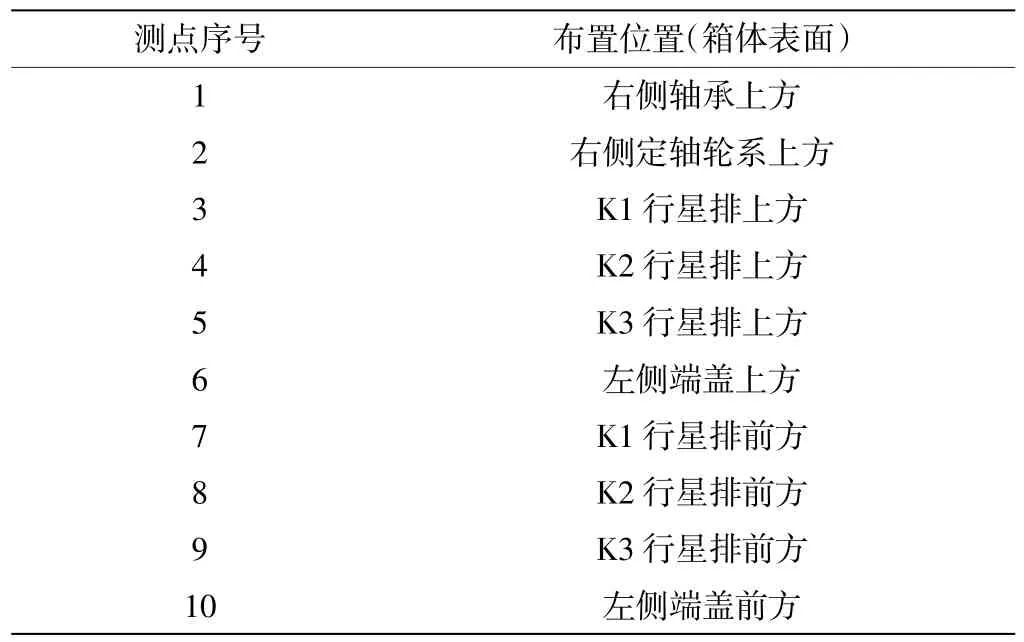
表1 仿真测点位置说明

表2 各档位行星排工作情况
选取输入转速为1500 r/min,仿真时长2 s,采样点数20 000。以K3 排Z30 太阳轮剥落为例,部分测点振动信号如图6 所示。
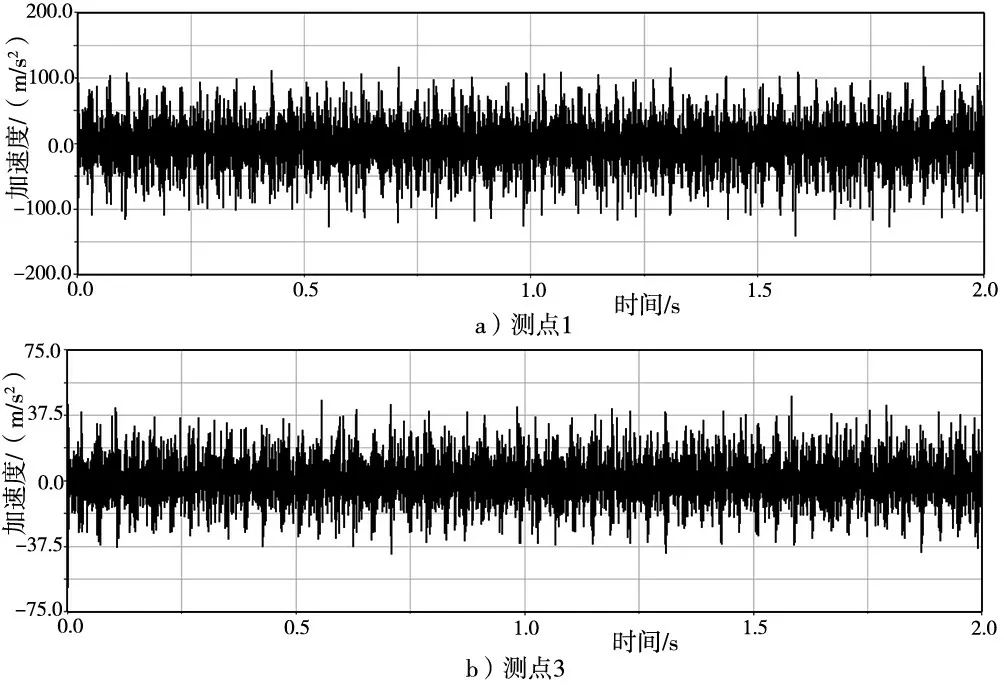
图6 K3 排Z30 齿轮剥落状态下的测点仿真加速度信号
2.3 测点优化
通过计算同一状态下各测点的时域特征参量构成高维特征空间。提取包括最大值、最小值、峰峰值、均方根值、方差、方根幅值、绝对平均幅值在内的7 个有量纲参数[12]和偏斜度、峭度、样本熵、波形指标、峰值指标、脉冲指标、裕度指标、峭度指标8 个无量纲幅域参数,构成1015 的高维特征矩阵。以K3 排Z30 太阳轮齿轮剥落故障为例,构成高维特征矩阵见表3。
运用局部线性嵌入算法对高维特征矩阵进行降维,为使数据降维结果更加直观且包含更多特征信息,目标维数设置为3。由于近邻数k 的取值目前仍无较好的确定方法[13],多次取值计算后发现,当k 取8 时,可以取得较为合理的低维流形,因此本文取k=8。
降维计算后K3 排Z30 太阳轮齿轮剥落故障各测点的低维坐标及2-范数计算结果见表4,降维后的矢量分布图如图7 所示。
计算后得到变速箱4 种状态下初步选择的10 个测点的敏感度排序,其敏感度按2-范数值由大到小排列,最终排序结果见表5。
从整体来看,位于箱体右侧轴承上方的测点1 敏感度最高,这是因为振动信号的传递路径是从齿轮传递到输出轴,再经过轴承传递到箱体表面,而测点1 位于箱体与行星传动轮系的连接处,所以采集到的振动信号较为剧烈,对故障特征信息最为敏感;位于箱体K3 排前方和左侧端盖前方的测点9、测点10 敏感度最低,虽然两测点距轴承较近,但由于箱体底部加强筋的缓振作用,其振动信号较为微弱,降低了对故障特征的敏感度。
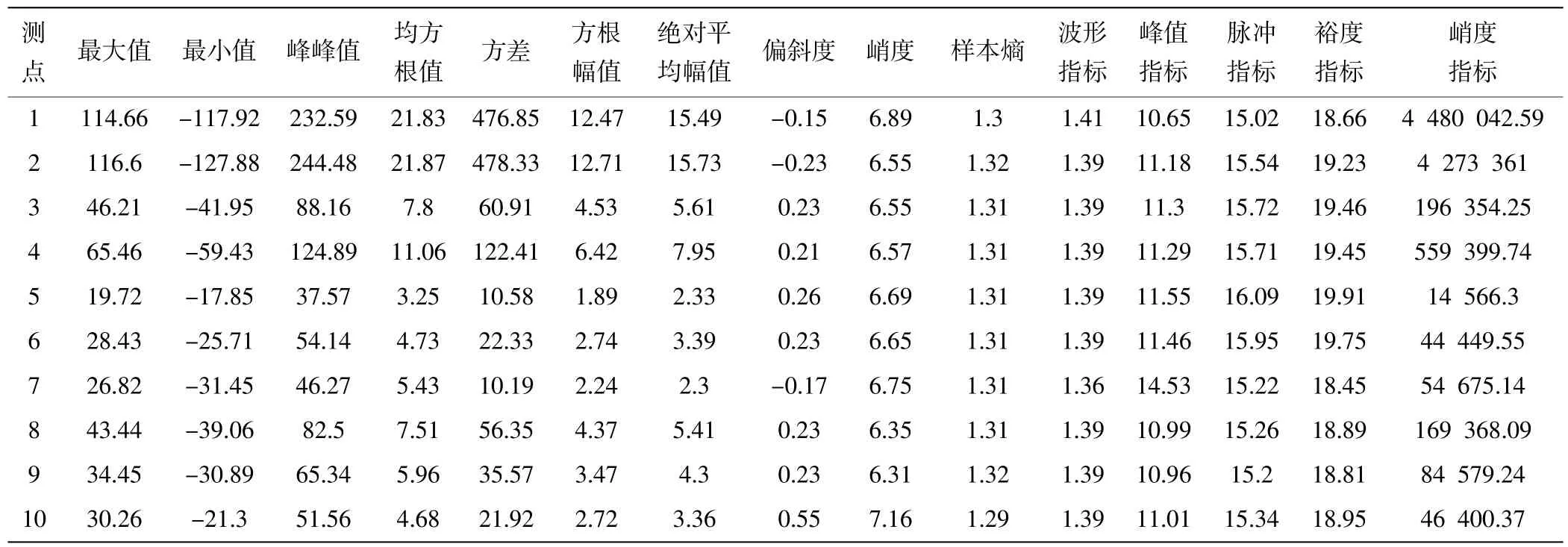
表3 Z30 齿轮剥落时各测点高维特征矩阵(有量纲参量单位:m/s2)

表4 Z30 齿轮剥落时各测点低维坐标值
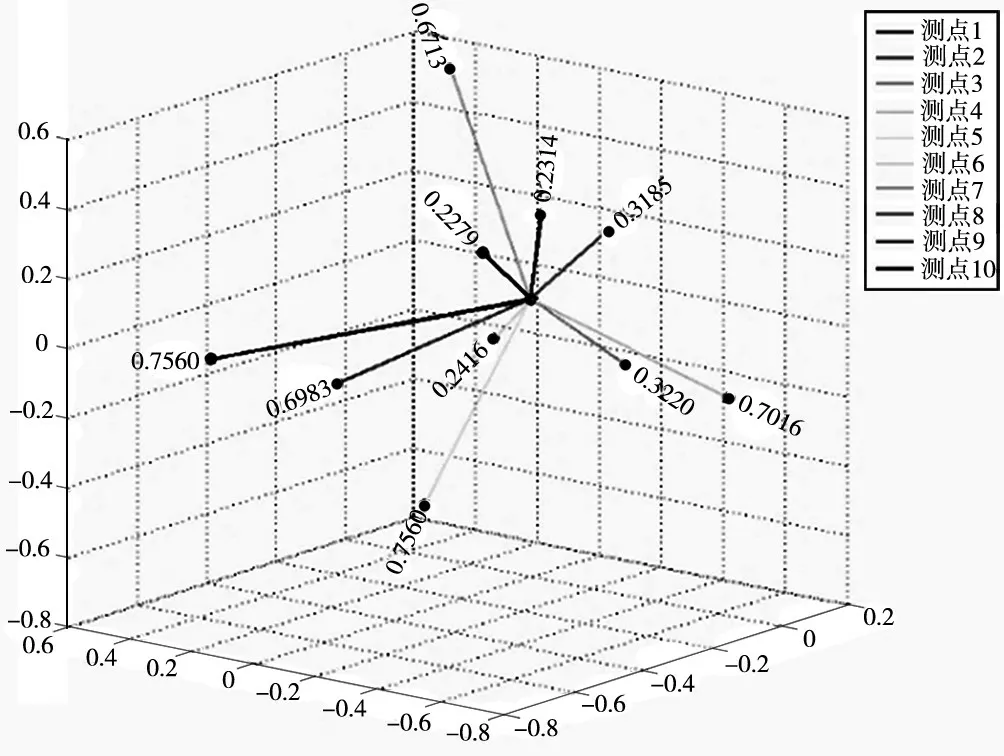
图7 降维后各测点矢量分布图

表5 测点敏感度排序
相对于箱体上方的测点3、4、5,箱体前方的测点7、8 的敏感度较低,同样箱体底部加强筋的缓振作用导致的。当故障位于不同的行星排时,靠近故障行星排的箱体上方测点敏感度较高;测点2 与测点1 的时域特征参量和降维后矢量分布相似度较高,但测点2 对振动信号信息的敏感度低于测点1。
基于上述分析结果,考虑到传感器数量限制和可行性,台架试验选取箱体右侧轴承上方的测点1、K1 行星排上方的测点3、K3 行星排上方的测点5,以及左侧端盖上方的测点6 为传感器布置点,开展对4 个测点的故障诊断效果对比研究。
3 试验验证
3.1 振动数据采集
行星变速箱试验台根据其工作原理进行设计,采用三相电机为动力源,电机额定功率110 kW,可提供转速范围为0~1500 r/min;利用换向传动箱将电机动力垂直换向后传至离合器,离合器实现运转中换挡操作。此外还配备了液压站为变速箱液压换挡提供液压动力。齿轮故障模拟与1.3 中一致,如图8 所示。

图8 齿轮故障实物模型
根据动力学仿真和测点优化结果,选取测点1、测点3、测点5、测点6 为传感器布置点,安装位置均位于箱体表面。试验台传感器布置信息见表6。
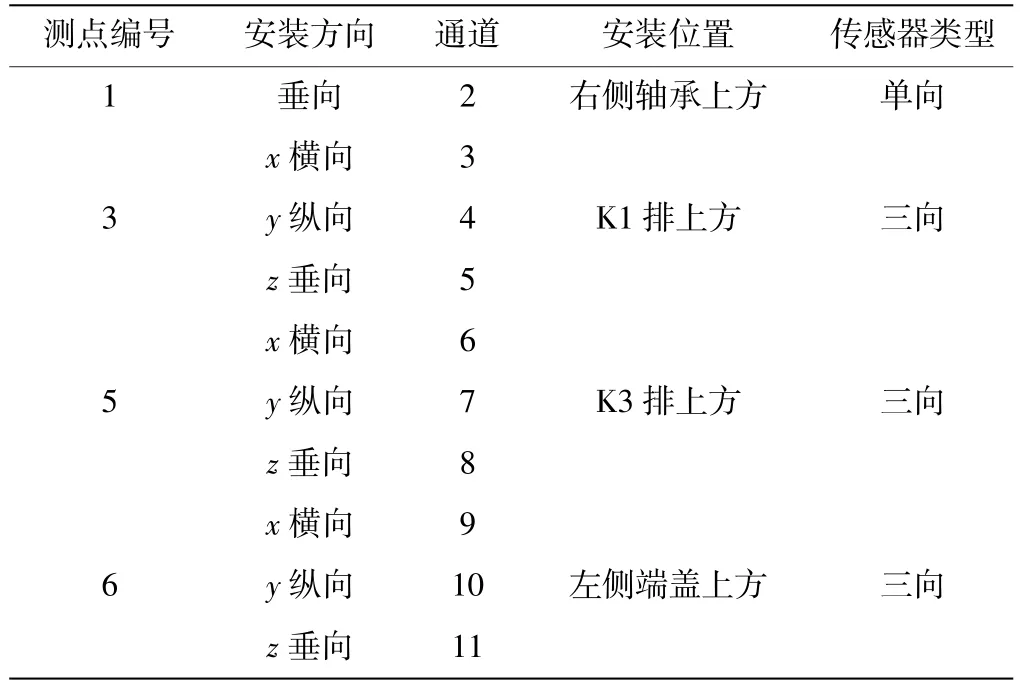
表6 振动传感器测点编号及安装位置
3.2 故障诊断
动力学仿真各测点振动数据运用局部线性嵌入算法降维之后,用2-范数描述测点对振动状态敏感度,2-范数值越大,表明测点对振动状态的敏感度越高[14]。为验证测点优化方案的有效性,选取4 个测点的实测振动信号,运用BP 神经网络算法进行故障诊断,具体步骤如下:
(1)对采集的实测振动信号进行时域特征提取,构成输入矩阵。选取的时域特征参照2.3 中的15 个参量,每个测点数据分为100 组,每组6000 个数据点,对3 个故障状态和正常状态各计算100 个样本,共400 个样本构成15400 的输入矩阵,见表7。
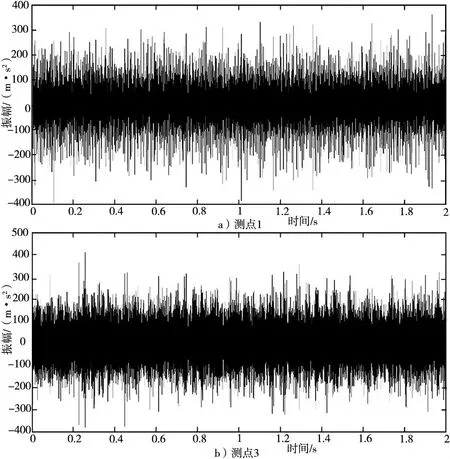
图9 Z30 剥落状态下的测点实测幅值信号
(2)设置BP 神经网络算法模型参数。随机抽取输入矩阵400 个样本的70%(280 个)设置为训练集,随机抽取15%(60个)的样本为验证集用来调整模型参数,随机抽取15%(60 个)的样本为测试集,对该测点的故障识别准确率进行评价,取20次测试的平均值为最终故障识别准确率,结果见表8。
(3)对最终结果进行分析。由表8 可知,测点故障识别准确率排序为测点1,测点3,测点5,测点6。测点对故障的识别准确率可反映为所采集的振动信号所包含故障信息的有效性,间接反映为测点对齿轮故障振动特征的敏感度。从结果来看,测点1 的采集的振动信号对故障特征的敏感度最高;测点3 与测点5 对故障特征的敏感度相近,但对不同故障的敏感度不同,由于4 种状态中有2 种状态位于测点3 下方K1 行星排,所以表现为测点3 的故障识别准确率略高于测点1;相对于其他3 个测点,测点6 的故障识别准确率最低,其虽靠近K3 行星排,但是因为行星变速箱的轴向振动受限,且最靠近箱体底部加强筋,所以振动信号所包含的故障特征较少。

表7 测点1 输入矩阵(有量纲参量单位:m/s2)

表8 各测点故障识别准确率
对照测点优化仿真结果,说明局部线性嵌入算法所计算出的低维流形虽然对单个状态的测点敏感度描述存在偏差,但是综合多种状态下能够有效地反映测点对振动信号故障特征的敏感度。
4 结束语
以某型行星变速箱为对象,根据正常状态与3 种不同的故障状态,在ADAMS 中建立其传动轮系-箱体的刚柔耦合模型,应用局部线性嵌入算法对其进行测点优化分析。在仿真数据的指导下,依托行星变速箱试验台采集实测振动数据,并借助BP神经网络算法对4 种不同状态下的测点数据进行故障识别准确率计算,验证了局部线性嵌入算法对行星变速箱测点优化的有效性与可靠性,具有较高的工程实践价值。
提出的基于局部线性嵌入的测点优化方法可以为开展台架试验提供理论指导和思路设计。鉴于当前一般对行星变速箱选取单一内部测点开展故障诊断研究,本文提出的方法为只有外部测点布置条件的行星变速箱及实车试验提供了最优测点选取思路,也可以通过分析降维后的流形分配权重,实现多测点融合的故障诊断方法。
