基于Hamilton能量理论的飞轮储能系统比率一致性控制
2020-09-24缪永来陈献慧曹智杰
王 冰, 缪永来, 陈献慧, 李 伟, 曹智杰
(1.河海大学能源与电气学院,江苏 南京 211100; 2.南京豪庆信息科技有限公司,江苏 南京 211100)
近年来,光伏、风电等可再生能源发展迅速,但是由于可再生能源本身具有间歇性和波动性,如果直接接入电网,会严重影响电网的电能质量[1-4],储能是解决这一问题的重要方法。作为一种新型储能技术,飞轮储能系统(flywheel energy storage system, FESS)被广泛应用于风力机的功率平滑、电能质量调节和电压恢复中[5-8]。
FESS是由多个飞轮储能单元组成的储能系统。目前已经有了一些关于FESS与风电场之间协调控制的研究成果[9-11],但是很少有涉及FESS内部的功率分配问题。王磊等[9]提出了一种FESS的充电、放电及安全协调控制策略。周龙等[10]介绍了一种将FESS应用于解决电网电压跌落的问题的方法。Itani等[11]给出了一种可行的FESS放电策略。对于大量配备在FESS中的飞轮储能单元,如何合理地分配它们之间的功率也是一个值得研究的问题。对于初始状态不同的飞轮储能单元来说,当飞轮在充电、放电过程中反复切换时,比率因子一致是其工作寿命的保障。本文基于一致性的基础,通过飞轮储能单元转速的调节实现比率因子的一致,确保飞轮储能单元可以按照同一比率进行能量的储存和释放,达到延长飞轮储能单元寿命的目的。
Hamilton能量方法是一种明确物理背景和工程意义的设计方法,它从能量角度为非线性系统的控制提供了有效的途径[12-13]。本文针对飞轮储能单元端口受控耗散Hamilton (port-controlled Hamilton with dissipation,PCH-D)系统,应用Hamilton能量理论中能量成型方法[14],通过改变能量函数实现飞轮储能单元的转速调节。 本文基于Hamilton能量成型的控制策略,通过飞轮储能单元转速调节实现比率因子的同步,使每个飞轮储能单元以同一比率储存和释放能量,实现FESS内部功率的合理分配。
1 问 题 描 述
由于风能的随机性和间歇性,风电场所发出的电能具有波动性。为平滑风电场的输出功率,可在风场接入大型储能装置,下面介绍风电场与飞轮储能系统的功率关系。
风电场实际释放功率与参考功率之差即为飞轮储能系统应该释放和存储的功率:
ΔP=Pw-P*
(1)
式中:P*——上层的指令参考功率;Pw——系统实际释放的功率;ΔP——FESS储存和释放的功率。
当ΔP>0时,FESS充电;当ΔP<0时,FESS放电。
1.1 比率因子的定义
比率因子定义为飞轮储能单元充电、放电裕量与充电、放电功率之比。飞轮储能单元的充电裕量[15]定义为
(2)
式中:ychar_i——飞轮储能单元的充电裕量;Ei——第i个FESS单元的充电终端存储能量,与飞轮的转速有关;Ei0——第i个FESS单元初始状态储存能量;t——时间。
对于飞轮储能单元来说,其充电、放电功率表达式为
P=τeΔω
(3)
式中:P——FESS单元充电、放电的功率;τe——FESS单元的电磁转矩;Δω——FESS单元充电、放电过程转速的变化。
飞轮储能单元存储能量的表达式为
(4)
式中:Jf——FESS单元的转动惯量;ωi——第i个FESS单元的转速。
根据比率因子的定义,把飞轮储能单元初始转速定义为ωi0,充电过程可达到的能量记为Eic,对应的飞轮转速为ωic,则每个飞轮储能单元充电时的比率因子rchar_i为
(5)
1.2 比率一致性
对于FESS来说,确保每个飞轮储能单元的比率因子一致是有效工作的保证。这时,飞轮储能单元按照同一比率进行能量的释放与储存,不仅能完成FESS内部功率的分配任务,而且可起到延长飞轮储能单元寿命的作用。对于充电过程的飞轮储能单元来说,实现比率一致性需要满足的条件为
(6)
对于转动惯量和负载转矩相同的飞轮储能单元来说,要实现飞轮以同一比率存储能量,满足的条件为
ωi0+ωic=T1
(7)
式中:T1——一常数值,表示飞轮储能单元充电时的初始转速和期望转速之和恒定。
2 飞轮储能单元的数学模型
以永磁同步电机作为飞轮驱动电机,在d-q坐标下飞轮储能单元充电时的数学模型可表示为[16]
(8)
式中:ufd——电机的d轴电压;ufq——电机q轴电压;Rs——定子电阻;ifd——电机d轴电流;ifq——电机q轴电流;Lfd、Lfq——电机d轴、q轴电感(满足Lfd=Lfq);Φ——电机转子的磁链;np——电机的极对数;Jf——转动惯量;τe——电机的电磁转矩;τL——负载转矩。这里,ifd、ifq、ω是状态变量,ufd和ufq是输入变量。
2.1 飞轮储能单元充电时的Hamilton模型
针对式(8),选飞轮储能单元的Hamilton能量函数为
(9)
其中x1=Lfdifdx2=Lfqifqx3=Jfω
基于以上Hamilton能量函数,式(8)可以表示为PCH系统形式如下:
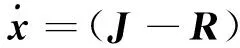
(10)


2.2 平衡点的确定和反馈控制器的设计
当负载转矩已知时,对于给定的转速ω0,可得飞轮储能单元的平衡点x0为[17]
x0=[x10x20x30]T=[0LfqτL/npΦJfω0]T
(11)
当负载转矩已知时,对于给定的转速ω0,可得平衡点的飞轮储能单元的反馈控制器αc(x)[17],则对应的PCH-D模型为
(12)
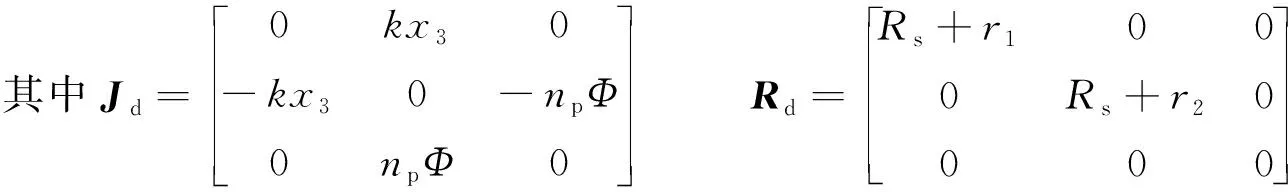
式中:yd——FESS基于平衡点的输出;μc—— 能量成型控制策略;r1、r2——第1个和第2个飞轮储能单元的比率因子。
3 FESS的能量成型控制策略
FESS依据上层的功率分配指令转化为飞轮储能单元的转速指令,通过能量成型控制策略达到所需指令的要求。飞轮储能单元能量成型的主要思路为:已知当前的Hamilton函数为Hd(x),对应的输出为yd=GTHd(x);而期望的Hamilton函数为Hr(x),对应的输出为yr=GTHr(x),则能量成型控制策略需要满足[15]。
yr=GTHr(x)=yd+d
(13)
其中yd=[ifd-ifd0ifq-ifq0ω-ω0]T
yr=[ifd-ifd0+d1ifq-ifq0+d2ω-ω0+d3]T
式中:yr——系统期望的输出;d——常数向量,表示飞轮接收上层指令后的调整量,d1、d2和d3对应ifd、ifq和ω的调整参数,设定d1=d2=0,通过调节d3的值实现转速的调节。
设计飞轮储能单元的能量成型控制策略为μc,在其作用下式(12)可改为
(Jd-Rd)Hd(x)+Gμc=(Jd-Rd)Hr(x)
(14)
注意到式(10)中G为列满秩矩阵,能量成型控制策略可表示为
μc=(GTG)-1GT(Jd-Rd)(Hr(x)-Hd(x))
(15)
基于以上过程,设计飞轮储能单元的控制策略,可得到以下定理。
定理1:考虑飞轮储能单元充电时的PCH-D模型式(12),基于能量成型方法,设Hamilton能量控制策略为
(16)
使得系统模型式 (12)在新的Hamilton函数Hr(x)下满足式(13),飞轮储能单元的输出达到指令所给的参考值。
飞轮储能单元的比率因子与飞轮储能单元的转速和电磁转矩有关。对于恒定负载转矩的飞轮储能单元来说,其比率一致性控制转化为飞轮储能单元转速的调节问题。针对不同初始转速的飞轮储能单元,应用能量成型控制策略,使其转速满足式ωic+ωi0=T1,进而实现比率一致性的控制目标。
4 仿 真 实 现
以与风电场相连的FESS为例进行MATLAB仿真。FESS包含6台飞轮储能单元,在负载转矩τL=5 N·m的条件下运行。FESS有2种工作模式,当ΔP=2 700 kW和ΔP=-3 200 kW时,FESS分别工作在充电与放电模式下。当ΔP>0时,6个比率因子收敛于一个正数,意味着6个飞轮储能单元以同一比率储存能量;ΔP<0时,6个比率因子收敛于一个负数,意味着6个飞轮储能单元以同一比率释放能量。

图1 充电、放电模式下FESS转速输出曲线 Fig.1 Output curves of rotate speed of FESS in charging and discharging modes
4.1 充电、放电模式下FESS的比率一致性
当FESS工作在充电模式下,即当ΔP=2 700 kW,转化为转速的调节指令。在6个飞轮初始转速分别为100 rad/s、80 rad/s、90 rad/s、120 rad/s、110 rad/s、130 rad/s时,在能量成型控制策略的作用下,转速输出如图1中红色曲线所示。
从图1中红色曲线可以得出:在0~20 s内,为飞轮初始转速输出曲线;20 s之后,当ΔP=2 700 kW,FESS充电,在能量成型控制策略作用下,取d3=[-100 -140 -120 -60 -80 -40]T,飞轮储能单元按照同一比率储存能量。其比率因子的输出曲线如图2中红色曲线所示,在0~20 s内,FESS工作在保持状态,其比率因子为0;20 s之后,当ΔP=2 700 kW,飞轮工作在充电状态,经过转速的调节,系统以同一比率因子充电。

图2 充电、放电模式下FESS比率因子输出曲线Fig.2 Output curves of ratio factors of FESS in charging and discharging modes

图3 充电、放电切换模式下FESS转速输出曲线Fig.3 Output curves of rotate speed of FESS during process of switching in charging and discharging modes

图4 充电、放电切换模式下FESS比率因子输出曲线Fig.4 Ratio factor curves of FESS during process of switching in charging and discharging modes
当FESS工作在放电模式下,即当ΔP=-3 200 kW,转化为转速的调节指令。在6个飞轮初始转速分别为200 rad/s、220 rad/s、180 rad/s、210 rad/s、160 rad/s、190 rad/s时,在能量成型控制策略的作用下,转速输出如图1中蓝色曲线所示。
从图1中蓝色曲线可以得出:0~20 s内,为飞轮初始转速输出曲线;20 s之后,当ΔP=-3 200 kW,FESS进行充电,能量成型控制策略作用下,分别取d3=[120 160 80 140 40 100]T,使飞轮储能单元按照同一比率进行释放能量。其比率因子的输出曲线如图2中蓝色曲线所示,在0~20 s内,FESS工作在保持状态,其比率因子为0;20 s之后,当ΔP=-3 200 kW,飞轮工作在放电状态,经过转速的调节,系统以同一比率因子进行放电。
4.2 充电、放电切换模式下FESS的比率一致性
实际应用中,FESS频繁工作在充电和放电的切换中。以6个飞轮储能单元组成的FESS为例说明。假定FESS在前20 s工作在初始转速状态;20 s之后取ΔP=3 200 kW;40 s后取ΔP=-2 100 kW;在6个飞轮储能单元的初始转速分别为100 rad/s、80 rad/s、90 rad/s、120 rad/s、110 rad/s、130 rad/s时,在能量成型控制策略下,FESS的转速输出结果如图3所示。
从图3的仿真结果可得:0~20 s内,为飞轮储能单元的初始转速曲线;20 s之后,当ΔP=2 700 kW,FESS工作在充电模式下,能量成型控制策略下,取d3=[-100 -140 -120 -60 -80 -40]T,可使飞轮储能单元按照同一比率进行储存能量,实现上层功率指令的有效分配;40 s之后,当ΔP=-2 100 kW,FESS工作在放电模式下,在能量成型控制策略作用下,取d3=[80 120 100 40 60 20]T,可使飞轮储能单元按照同一比率进行释放能量,转速输出曲线也反映出能量状态的变化,实现上层功率指令的有效分配。其比率因子的输出仿真如图4所示。
从图4的仿真结果可得:0~20 s,FESS工作在保持状态,飞轮储能单元的比率因子为0;20~40 s,FESS以同一比率因子充电;40 s之后,FESS从充电模式切换到放电模式下,FESS以同一比率因子放电。
5 结 语
本文研究FESS的功率分配问题,基于Hamilton能量成型的控制策略,通过飞轮储能单元的转速调节实现比率一致,进而实现功率的有效分配。从理论角度出发,将比率一致性控制转变为对FESS的转速调节,基于转化的思想,实现功率的有效分配。理论分析和仿真验证可知,比率一致性控制下,可以对FESS进行有效的功率分配和控制。
