Q235缺陷试件力-磁量化关系的仿真与实验研究

于凤云， 郭绍炳， 刘锦辉， 唐庆菊， 胡金平， 冯明军

(1.黑龙江科技大学 研究生学院， 哈尔滨150022； 2.黑龙江科技大学 机械工程学院， 哈尔滨 150022)

0 引 言

铁磁性材料构件在航空、电力、煤矿等众多领域有着广泛应用，由于铁磁性材料不断受到外力作用，其内部不可避免的会产生微裂纹及应力集中现象。根据某项针对工业领域设备结构的调查，承载结构服役寿命的长短，主要取决于构件初始损伤累积阶段，这一阶段约占整个在役寿命的 80% 以上[1]。因此，为防止生产中重大安全事故发生，对铁磁性材料构件安全性能进行及时有效监测显得尤为重要。铁磁性材料构件在设备运转过程中，由于受载荷作用，应力集中区域磁畴组织会发生定向和不可逆的重新取向[2]。金属磁记忆检测技术是建立在这种特性的一种有效判断缺陷的检测手段。

国内外研究人员对铁磁性材料磁记忆特性与温度对试件表面磁场强度大小的影响进行了诸多研究，利用ANSYS仿真发现当试件温度小于居里点时，磁场信号变化较小，而当试件温度在居里点附件时，磁场强度曲线峰峰值则急剧增大，但是曲线的变化趋势没有改变[3-4]。樊清泉[5]针对外部磁场强度的影响，以含圆孔试件为分析对象，通过研究改变外加磁场和地磁场的相对方向得出，当外加磁场与地球磁场方向一致时，外加磁场和磁场强度为正相关，反之，则为负相关。钱康[6]研究铁磁性试件弹塑性阶段的磁场信号，提出贯穿试件全部区域的力磁耦合理论模型，采用ANSYS分析软件仿真发现，当试件处于塑性变形阶段时，磁场信号发生锐变现象。

笔者以含圆孔缺陷的Q235钢试件作为研究对象，提取试件表面切向磁场强度，分析切向磁场强度随拉伸应力的变化规律，得出应力与切向磁场强度之间的函数关系，并通过拉伸实验与模拟仿真进行对比，为金属磁记忆检测技术对构件应力的定量化评价提供理论依据。

1 仿真模型的建立

根据力-磁耦合模型，修改Q235试件在各个拉伸应力下的单元相对磁导率，建立通电螺线管模型，施加电流载荷，模拟地球环境磁场。在此基础上，选定模型划分单元，赋予模型区域属性，施加三维磁场边界垂直条件，提取缺陷试件在各个拉伸应力下的表面磁场强度。

1.1 单元类型

采用三维静态磁场标量法仿真分析Q235试件，选用三维磁标量实体单元SOLID96划分试件模型网格，该单元为正八面体，可为饱和区、永磁区和空气区建模，选用SOURCE36单元建立三维螺线管模型，该单元有杆状、弧状、线圈三种基元类型，文中采用杆状和弧状两种基元类型进行三维螺线管的建模。

1.2 地磁场模型

根据麦克斯韦基本方程理论，利用ANSYS分析软件中的Mechanical APDL模块进行仿真建模。模型中心线为x轴，线圈建立在y-z平面上。根据电磁学理论，空气磁导率μ0为1.256×10-6，模拟线圈内部磁场大小为39.8 A/m，参数设置螺线管中心线到螺线管最右边的距离为0.012 m，螺线管中心线到螺线管最上边的距离为0.012 m，螺线管倒角处半径为0.002 m，螺线管内总的电流量为119.4 A·m，螺线管的总长度为3 m，螺线管管壁的厚度为0.002 m。

模型参数选定后，设置单元属性可见，建立三维螺线管模型如图1所示。

图1 三维螺线管Fig. 1 Modeling of spiral tube

建立圆柱形空气模型，在空气两端设置磁场垂直边界条件，求解后的磁场强度云图如图2所示。螺线管内大体为一均匀磁场，且磁场强度大小为39.8 A/m，符合模拟仿真所要求同等地磁场大小的条件。

图2 螺线管内部磁场Fig. 2 Internal magnetic field of spiral tube

1.3 试件模型

含圆孔缺陷Q235试件受到轴向拉伸载荷作用时，试件内部会逐渐形成微观缺陷并逐渐向四周扩散，在外部环境磁场作用下，其内部磁畴组织会发生重新并不可逆的取向，从而导致试件内部磁导率大小的改变。为研究其内在规律，分析试件拉伸后磁场强度变化特性，借鉴文献[7]的力-磁耦合模型为

(1)

式中:Bm——饱和磁感应强度，T；

σ——试件拉伸应力，Pa；

λm——饱和磁致伸缩系数；

μr——初始相对磁导率。

根据式(1)求得，在不同拉伸应力下试件划分单元的相对磁导率。

试件设计为板状，总体尺寸为285 mm×35 mm×10 mm，试件中间圆孔缺陷直径φ8 mm、深度6 mm，如图3所示。

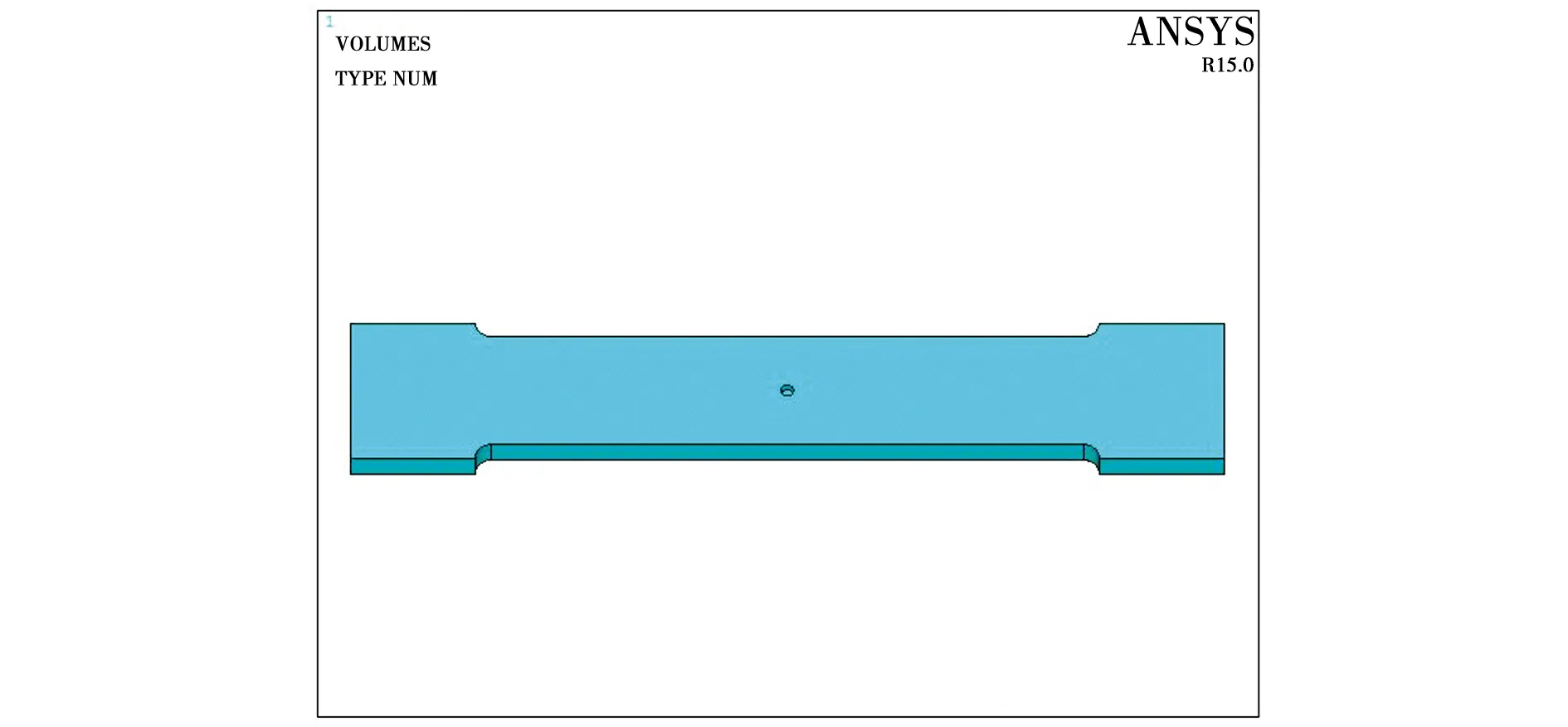
图3 仿真试件模型Fig. 3 Simulation specimen model

2 仿真与结果分析

根据仿真实验平台，设置仿真参数，建立单元磁导率数组文本文件，使用APDL循环语句DO-ENDDO命令修改单元相对磁导率，进行仿真。求解结束后，沿试件拉伸方向设置磁场强度提取路径，提取磁场强度切向分量，研究切向磁场强度随试件拉伸应力的变化规律，如图4所示。

图4 切向磁场强度与拉伸应力的关系Fig. 4 Relationship between tangential magnetic field strength and tensile stress

由图4可见，不同拉伸应力下切向磁场强度曲线均呈轴对称分布，在圆孔缺陷中心位置处，切向磁场强度出现最大值。同时，随着试件所受拉伸应力的增大，切向磁场强度峰值也在逐渐增加，而其每次增加幅度则有所减小。为探究切向磁场强度与拉伸应力之间的量化关系，进一步提取不同拉伸应力下的切向磁场强度峰值，其随拉伸应力的变化规律如图5所示。

图5 切向磁场强度峰值与拉伸应力关系Fig. 5 Relationship between peak intensity of tangential magnetic field and tensile stress

由图5可见，切向磁场强度峰值大小随拉伸应力的增加而逐渐增大，峰值变化较为明显，从最初35 A/m增大到119 A/m，而其在每次拉伸应力下峰值增幅则从26 A/m减小到10 A/m。总体而言，随着拉伸应力的增大，切向磁场强度峰值的增加趋于平缓，呈凸函数关系变化趋势，因此，在一定拉伸应力范围内，可对磁场强度峰值与拉伸应力之间进行二次函数拟合。

3 拉伸实验与结果分析

3.1 实验

拉伸实验平台由拉伸实验机、应力集中检测仪及拉伸试件组成。实验选用CMT5305微机控制实验机进行拉伸，如图6所示。在室温条件下，其恒力、恒变形、恒位移控制范围每秒加载对应参量满程的百分比为0.5%～5.0% ，最大拉力为300 kN。

图6 CMT5305微机控制实验机Fig. 6 CMT5305 microcomputer controlled testing machine

磁场强度测量仪器为TSC-3M-12应力集中检测仪，如图7所示。该仪器利用金属磁场强度法对试件应力集中情况进行测量、记录。

图7 TSC-3M-12 型应力集中检测仪Fig. 7 TSC-3M-12 stress concentration detector

预制与仿真实验相同尺寸的Q235试件，如图8所示。

图8 试件Fig. 8 Specimen

试件加载方式与仿真实验相对应，即试件最大截面处应力分别按照30、60、90、120、150、180 MPa的大小进行加载。

设置检测路径方向为试件长度方向，测量路径相对圆孔中心线偏移量为0。在每次拉伸后，采用TSC-3M-12应力集中检测仪，测量并提取切向磁场强度峰值，研究其在不同拉伸应力下的变化趋势。

3.2 结果分析

在每次拉伸试件后，设置提离值为2 mm，提取各应力下的切向磁场强度，如图9所示。从图9可以看出，切向磁场强度的变化趋势与仿真阶段相比具有很好的一致性。就单一应力下的切向磁场强度而言，在靠近圆孔缺陷处，切向磁场强度随拉伸应力增加逐渐增大，在圆孔缺陷中心位置处出现峰值；随着拉伸应力从30 MPa逐渐增大至180 MPa过程中，切向磁场强度峰值也在不断增加，但峰值增加幅度却在逐渐减小。远离圆孔缺陷处的切向磁场强度随拉伸应力的增加有增有减，其变化规律与仿真结果总体一致，但在远离缺陷处的具体量值变化上有不完全吻合之处，这是由于试样材料、制备工艺及实验条件等因素影响所致。

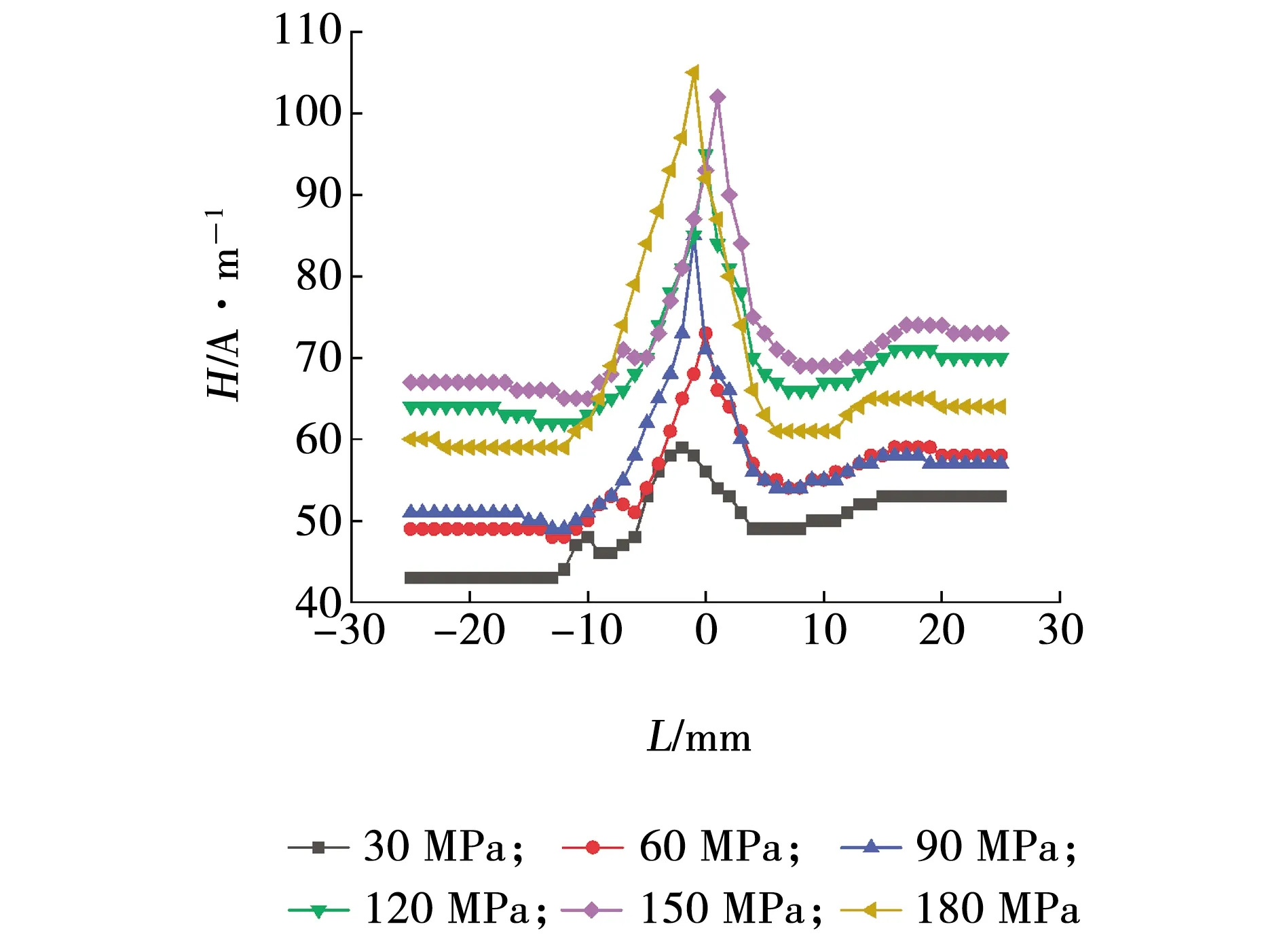
图9 切向磁场强度与拉伸应力关系Fig. 9 Relationship of tangential magnetic field intensity and tensile stress

为近一步研究切向磁场强度随拉伸应力变化的内在规律，提取不同应力下的切向磁场强度峰值如图10所示。由图10可见，不同拉伸应力下，切向磁场强度峰值最小为59 A/m，最大为105 A/m；峰值最大增幅在应力60 MPa时为14 A/m，最小增幅在应力为180 MPa时出现，为3 A/m，在拉伸应力由30 MPa增加至180 MPa过程中，切向磁场强度峰值增幅逐渐减弱。这主要是因为随着拉伸应力的增加，铁磁性构件内部磁畴组织，不可逆的重新取向得到进一步强化，导致更多的磁力线溢出试件表面；而当拉伸应力较大时，试件缺陷处的变形临近塑性变形，磁畴组织的不可逆取向趋于平衡，溢出试件表面的磁力线数有所减少，因此，切向磁场强度的增加幅度减缓，其切向磁场强度峰值变化曲线呈凸函数变化，并随着拉伸应力增加趋于某一稳定值。

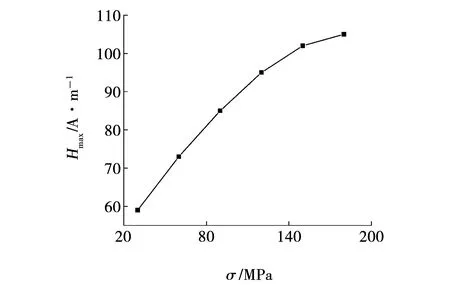
图10 切向磁场强度峰值与拉伸应力关系Fig. 10 Relationship between peak value of tangential magnetic field intensity and tensile stress

通过以上分析，拉伸实验获得的切向磁场强度峰值随拉伸应力的变化规律与仿真结果具有很好的一致性，在一定拉伸应力范围内，切向磁场强度峰值随拉伸应力的增加而逐渐增大，且增幅逐渐减小。拉伸实验测得的切向磁场强度数值与仿真的差异主要是由于试样制备、现场干扰信号等原因导致的。切向磁场强度峰值与拉伸应力之间的变化规律以凸函数关系呈现，可进行二次函数关系拟合。

根据以上分析，在试件所受拉伸应力180 MPa范围内，对其力-磁关系进行函数拟合，相关系数为

0.999 4，得到切向磁场强度峰值与拉伸应力之间的关系为

Hmax=-0.001 5σ2+0.623 9σ+41.3,

(2)

式中：Hmax——切向磁场强度峰值，A/m；

σ——拉伸应力，MPa。

因此，在工程实践中，可以参考切向磁场强度峰值与拉伸应力之间的函数关系，根据被测构件表面切向磁场强度峰值反推其所受拉伸应力大小，以此评估构件的受力状态，预测损伤情况。

4 结束语

切向磁场强度峰值与拉伸应力之间的变化规律在ANSYS仿真和拉伸实验中具有很好的一致性，即切向磁场强度峰值随拉伸应力增加而逐渐增大，切向磁场强度峰值增幅随拉伸应力增加逐渐减小，建立了切向磁场强度峰值与拉伸应力之间的拟合关系式。在工程实际中，根据切向磁场强度峰值与拉伸应力之间的量化关系，在测得表面切向磁场强度峰值基础上，可以反演构件所受拉伸应力大小，从而为铁磁性构件安全运行提供参考依据。