大倾角巷道掘进机截割过程整机滑移的力学模型

2020-09-24符世琛

黑龙江科技大学学报 2020年4期

宗凯，符世琛

(1.清华大学机械系，北京 100084； 2.中国矿业大学(北京) 机电与信息工程学院，北京 100083)

0 引言

我国煤炭资源的持续开采已经造成许多矿井的资源趋于枯竭，因此一些倾斜煤层的开采越来越受到重视。巷道掘进是煤炭开采最重要的环节之一，尤其是在深部倾斜煤层，掘进作业的难度更加突出。悬臂式掘进机是井下掘进工作面最重要的设备，主要用于巷道的挖掘，为布置采煤工作面做准备。掘进机在大倾角巷道掘进时，煤岩硬度不断变化，再加上倾斜煤层综掘工作面复杂的工作环境与作业条件，以及掘进机本身复杂的结构，导致掘进机在截割过程中整机位置不断变化，发生整机滑移现象，会影响掘进机的定位与定向掘进，降低巷道成形质量与掘进效率[1-7]。因此，研究大倾角巷道掘进机截割过程整机滑移响应规律，无论是对基础理论，还是实践指导，都有重要的价值。

国内外一些学者曾在相关方面做了一些研究。Zong等[8-9]通过动力学建模和仿真分析的手段，研究了掘进机横向截割过程机身位姿响应规律和截割臂摆角跳动规律。李晓豁[10]基于拉格朗日方程建立了随机激励作用下掘进机整机振动响应的数学模型，利用Matlab对该数学模型进行赋值求解，得到了随机激励作用下截割头、悬臂和机体的振动响应特性。Zhao等[11]基于拉格朗日方程建立了掘进机整机动力学模型，对掘进机截割过程中整机系统振动特性进行了分析，得到其振动频率及幅值响应结果。姚继权[12]基于拉格朗日方程建立了掘进机行走部振动响应的数学模型，通过仿真分析得到了掘进机行走部横向和纵向的振动特性。何洋[13]通过ProE建立了纵轴式掘进机三维实体模型，利用Adams对掘进机整机进行了模态分析，得到了不同工况下截割头、悬臂、机体的振动特性。蒲志新等[14]利用ProE建立了掘进机的三维实体模型，通过Adams对其进行模态分析，获得了截割头、悬臂、机体的纵向振动特性。

综上所述，已有的研究大多是针对掘进机整机或者一些关键结构进行模态分析和振动特性分析，笔者曾针对普通煤层研究了掘进机截割过程位姿变化规律[8,15]，而对于倾斜煤层这一特殊工况下掘进机截割过程中整机滑移响应特性的研究尚未见报道，因此，笔者将采用理论建模和仿真分析的手段，研究倾斜煤层掘进机截割过程整机滑移特性。

1 整机滑移动力学模型

掘进机整机的滑移通过偏向位移、后向位移和卧底位移三个变量来描述。截割头与截割臂之间的刚度用K1表示，阻尼用C1表示；截割臂与机体之间的刚度用K2表示，阻尼用C2表示；机体与底板地面之间的刚度用K3表示，阻尼用C3表示。截割头质量为m1，截割臂质量为m2，机体质量为m3(包括行走机构)。截割载荷可用三向力来描述，即水平方向、竖直方向和垂直于煤壁方向的力。掘进机在截割过程中的力学模型如图1所示。

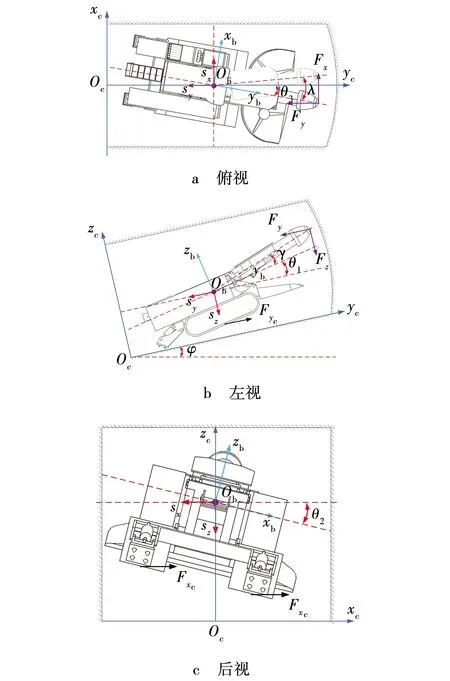
图1 掘进机力学模型Fig. 1 Mechanical model of roadheader

定坐标系Ocxcyczc为巷道空间坐标系，坐标系Obxbybzb固定于掘进机机身并随掘进机运动。xc轴表示水平方向，yc轴表示垂直于煤壁方向，zc轴表示竖直方向。φ为煤层倾角，λ为截割臂水平摆角，γ为截割臂垂直摆角，sx为整机在xc轴方向的位移，即偏向位移,sy为整机在yc轴方向的位移，即后向位移,sz为整机在zc轴方向的位移，即卧底位移,θ1为整机俯仰角,θ2为整机横滚角,Fx、Fy、Fz分别为截割载荷在水平方向、垂直于煤壁方向、竖直方向的分力,Fxc、Fyc分别为底板地面对履带部的沿xc轴、yc轴方向的摩擦力。

1.1 横向截割过程

截割作业过程中的掘进机可视为完整非保守系统，含有Rayleigh耗散函数的第二类Lagrange方程为[16]

(1)

式中:T——系统的动能；

D——系统的耗散能；

U——系统的势能；

qi——广义坐标；

i——广义坐标数；

Qi——广义力。

基于式(1)形式的Lagrange方程，计算出横向截割过程中掘进机系统的动能T、势能U和耗散能D，然后可得：

(2)

(3)

(4)

sx+K1sinθ2[Lsin(γ+φ-θ1)-Lsin(γ+φ)-bsinθ2+sysin(φ-θ1)+szcos(φ-θ1)]/cos2γ。

(5)

设系统的广义力为Qx，则

Qx=Fxc+Fx。

(6)

将式(2)～(6)代入式(1)，则偏向位移的运动微分方程为

(m1+m2+m3)gsinθ2-(m1L+m2Ly)cosγ·

φ-θ1)-Lsin(γ+φ)-bsinθ2+sysin(φ-

θ1)+szcos(φ-θ1)]}/cos2γ=Fx+Fxc。

(7)

同理可得，后向位移和卧底位移的运动微分方程为

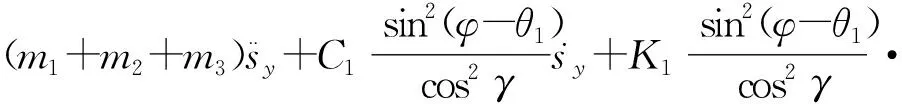
sy+(m1+m2+m3)gsin(φ-θ1)-(m1L+

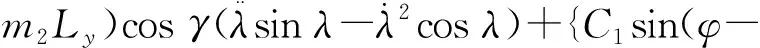
θ1)[Lsin(γ+φ-θ1)-Lsin(γ+φ)-bsinθ2+

szcos(φ-θ1)+sxsinθ2]}/cos2γ=Fy+Fyc，

(8)

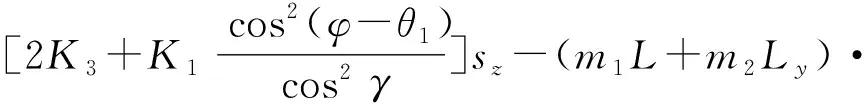
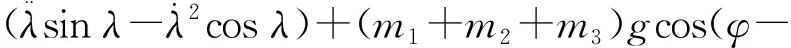
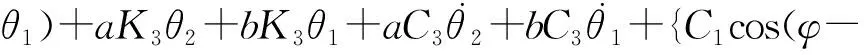
θ1)[Lsin(γ+φ-θ1)-Lsin(γ+φ)-bsinθ2+

sysin(φ-θ1)+sxsinθ2]}/cos2γ=Fz+G+FN。

(9)

式中：L——截割臂回转中心与截割头回转中心之间的距离；

Ly——截割臂的重心与其回转中心之间的距离；

Jx、Jy、Jz——掘进机机体绕xb、yb、zb轴的转动惯量；

a、b——掘进机机体宽度和长度的1/2；

G——掘进机自身重力；

FN——底板地面对掘进机的支反力。

式(7)～(9)即为掘进机横向截割过程中整机滑移动力学模型。

1.2 纵向截割过程

同理，基于式 (1)，计算出纵向截割过程中掘进机系统的动能，势能和耗散能，推导得到纵向截割过程掘进机整机滑移动力学模型为

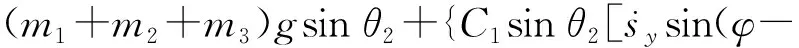
φ-θ1)-Lsin(γ+φ)-bsinθ2+sysin(φ-

θ1)+szcos(φ-θ1)]}/cos2γ=Fxc+Fx，

(10)

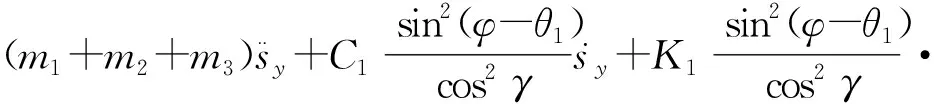
sy+(m1+m2+m3)gsin(φ-θ1)+{C1sin(φ-

θ1)[Lsin(γ+φ-θ1)-Lsin(γ+φ)-bsinθ2+

szcos(φ-θ1)+sxsinθ2]}/cos2γ=Fyc+Fy，

(11)

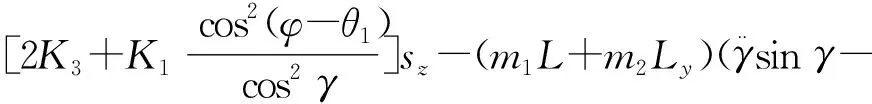
Lsin(γ+φ)-bsinθ2+sysin(φ-θ1)+

sxsinθ2]}/cos2γ=Fz+G+FN。

(12)

2 Simulink仿真模型

根据掘进机截割过程中整机滑移动力学模型，在Matlab/Simulink中建立求解微分方程组(1)的仿真模型，如图2所示。以EBZ-160型掘进机为例，通过相关计算和借鉴文献[17-18]，得到仿真初始参数如表1所示。

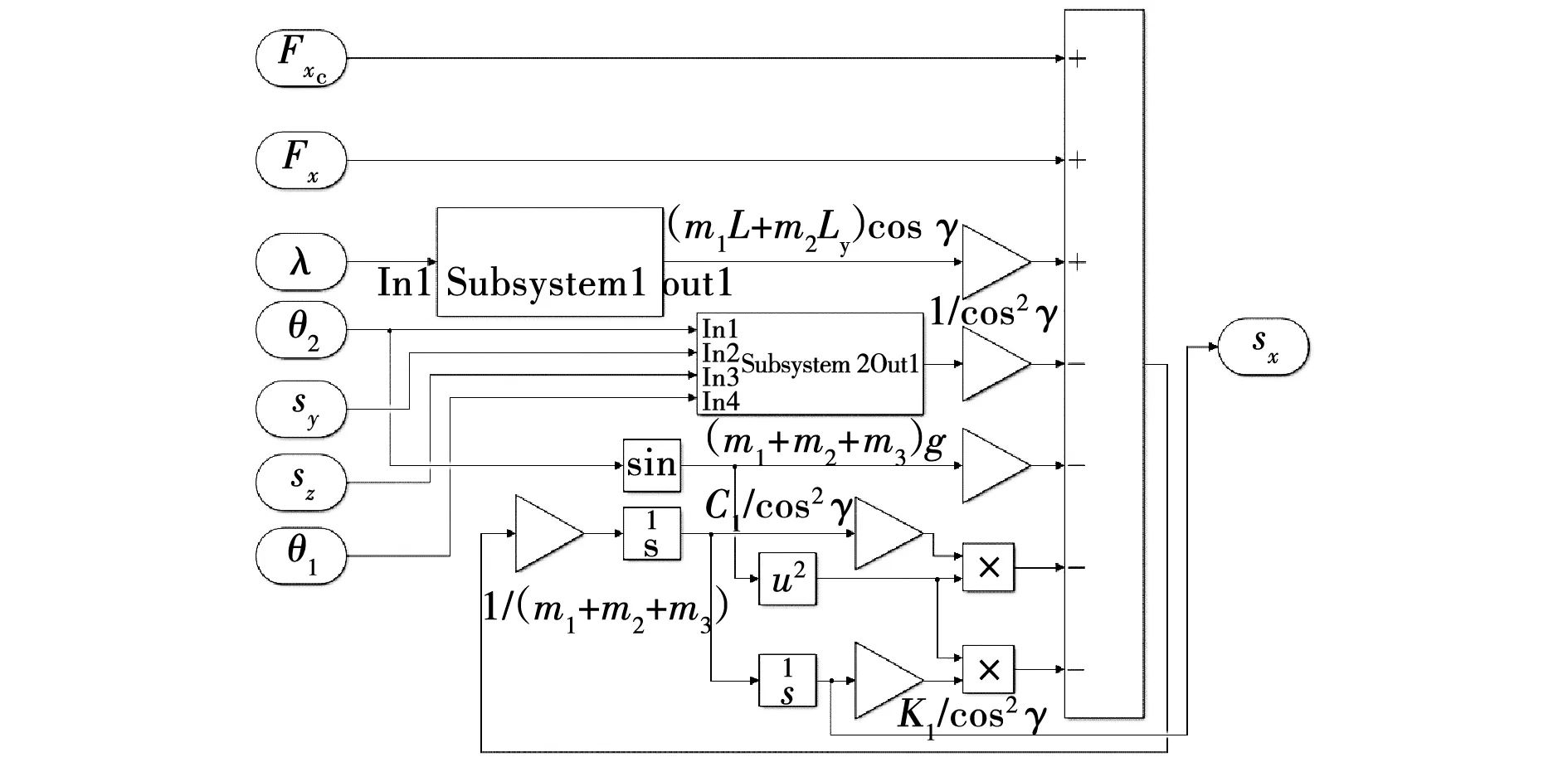
图2 Simulink仿真模型示例Fig. 2 Example of simulink model

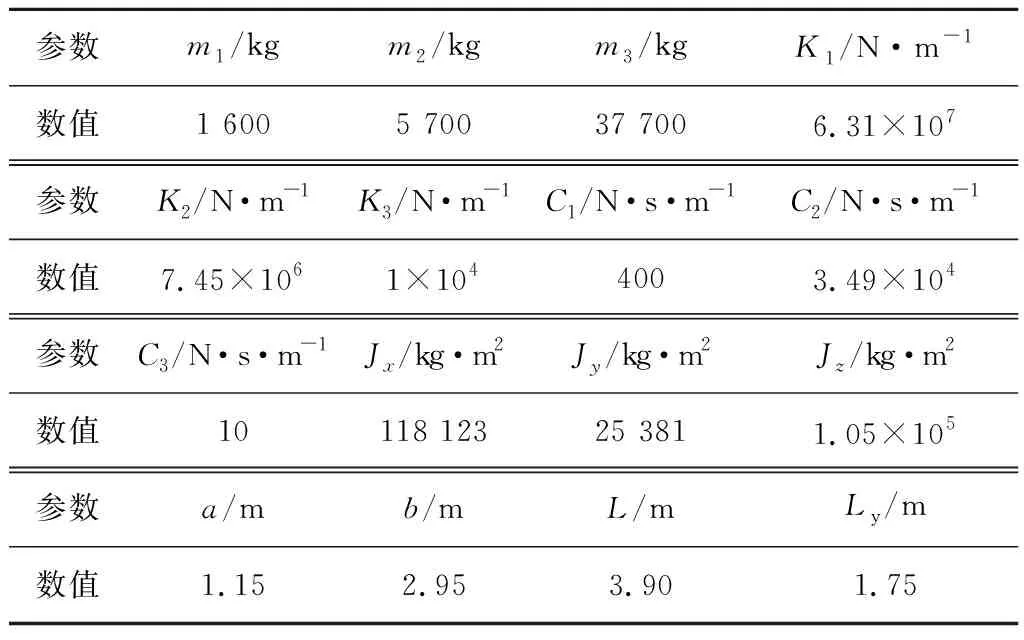
表1 仿真初始参数Table 1 Initial parameters of simulation

3 整机滑移响应

在煤地质学中，将倾角为25°～45°的煤层定义为倾斜煤层[19]。文中重点针对倾角为30°的大倾角巷道，利用Simulink仿真方法对横向和纵向截割过程中掘进机整机滑移动力学模型进行求解，分析整机滑移规律影响因素。

3.1 横向截割过程

横向截割过程中，截割臂水平摆角不断变化，而垂直摆角为一定值，对式(7)～(9)的求解结果进行参数分析，偏向位移、后向位移和卧底位移的响应结果分别如图3～5所示，煤层倾角对整机滑移的影响如图6所示。其中，截割载荷Fx、Fy和Fz是根据文献[6,7,13]中提出的截割载荷计算方法计算得到，具体计算过程文中不再赘述。

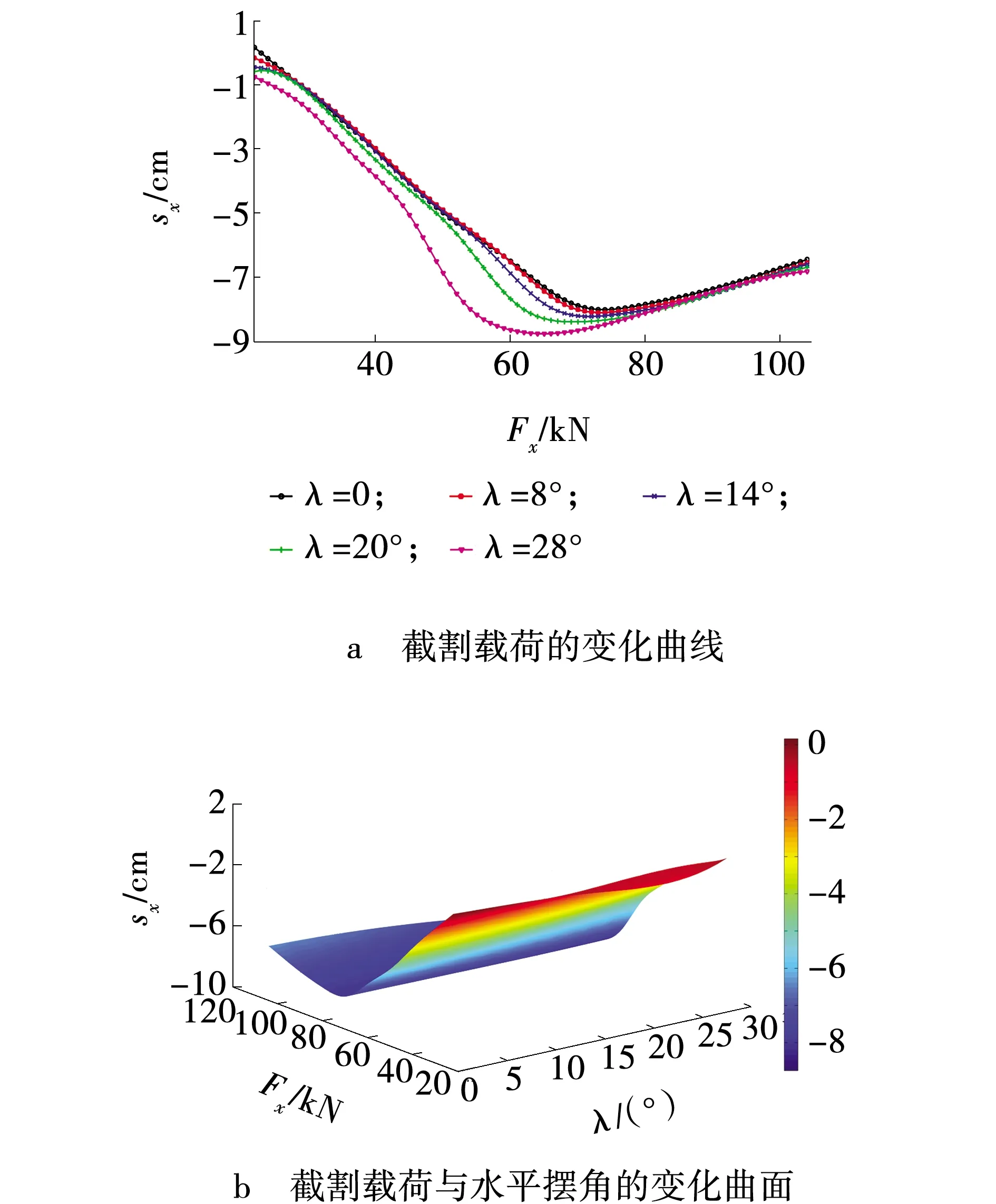
图3 偏向位移响应结果Fig. 3 Response result of lateral displacement

在横向截割过程中，截割载荷是掘进机发生整机滑移的主要因素，对滑移结果有巨大的影响，而截割臂水平摆角对整机滑移的影响却很轻微。在截割载荷的作用下，卧底位移变化最为显著，最大值可达14.6 cm；后向位移变化幅值最小，为4.5 cm；偏向位移的最大值为8.8 cm。在倾斜煤层的倾角范围内，偏向位移和后向位移随着巷道倾角的增大而增大，卧底位移随着煤层倾角的增大而减小。

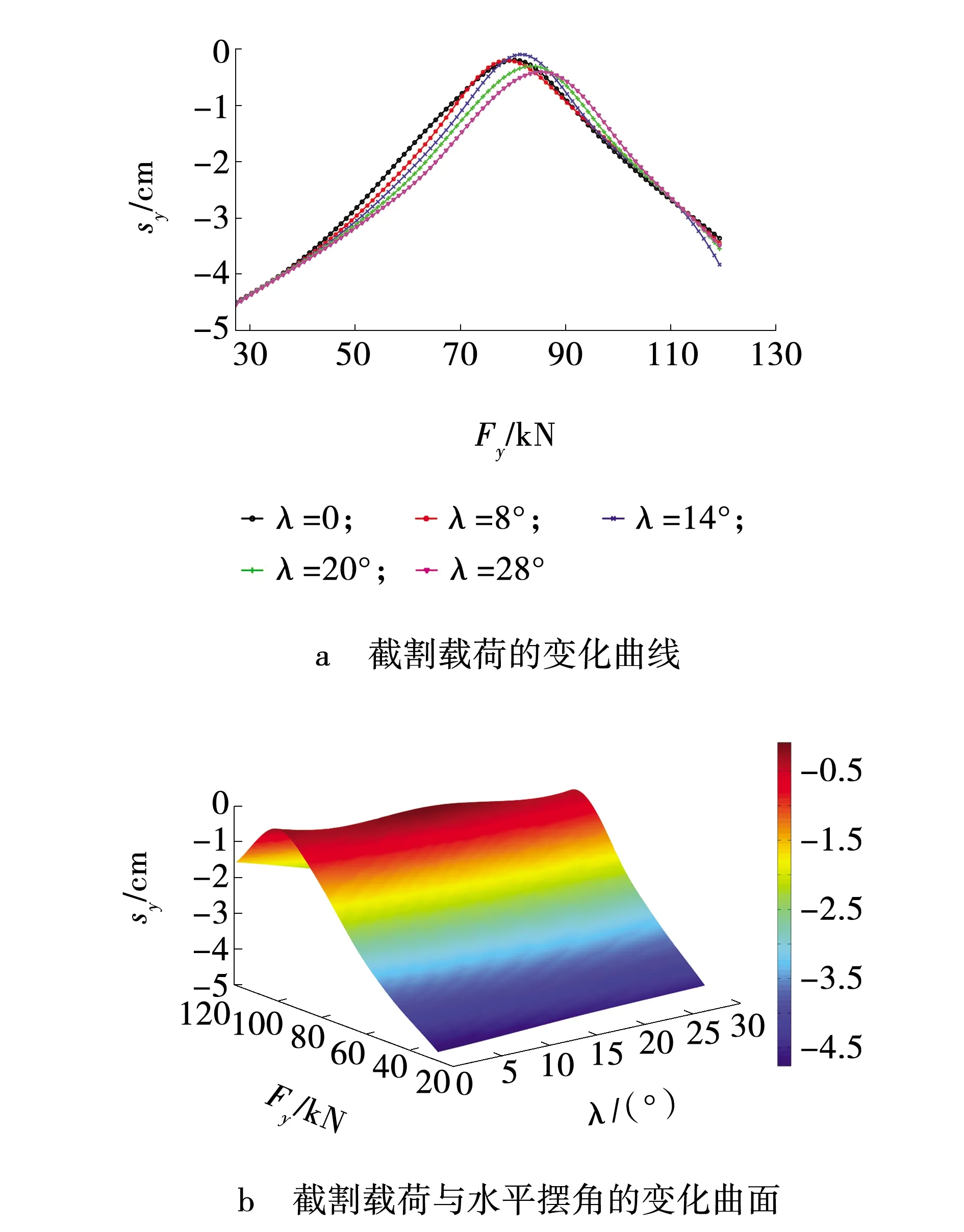
图4 后向位移响应结果Fig. 4 Response result of backward displacement

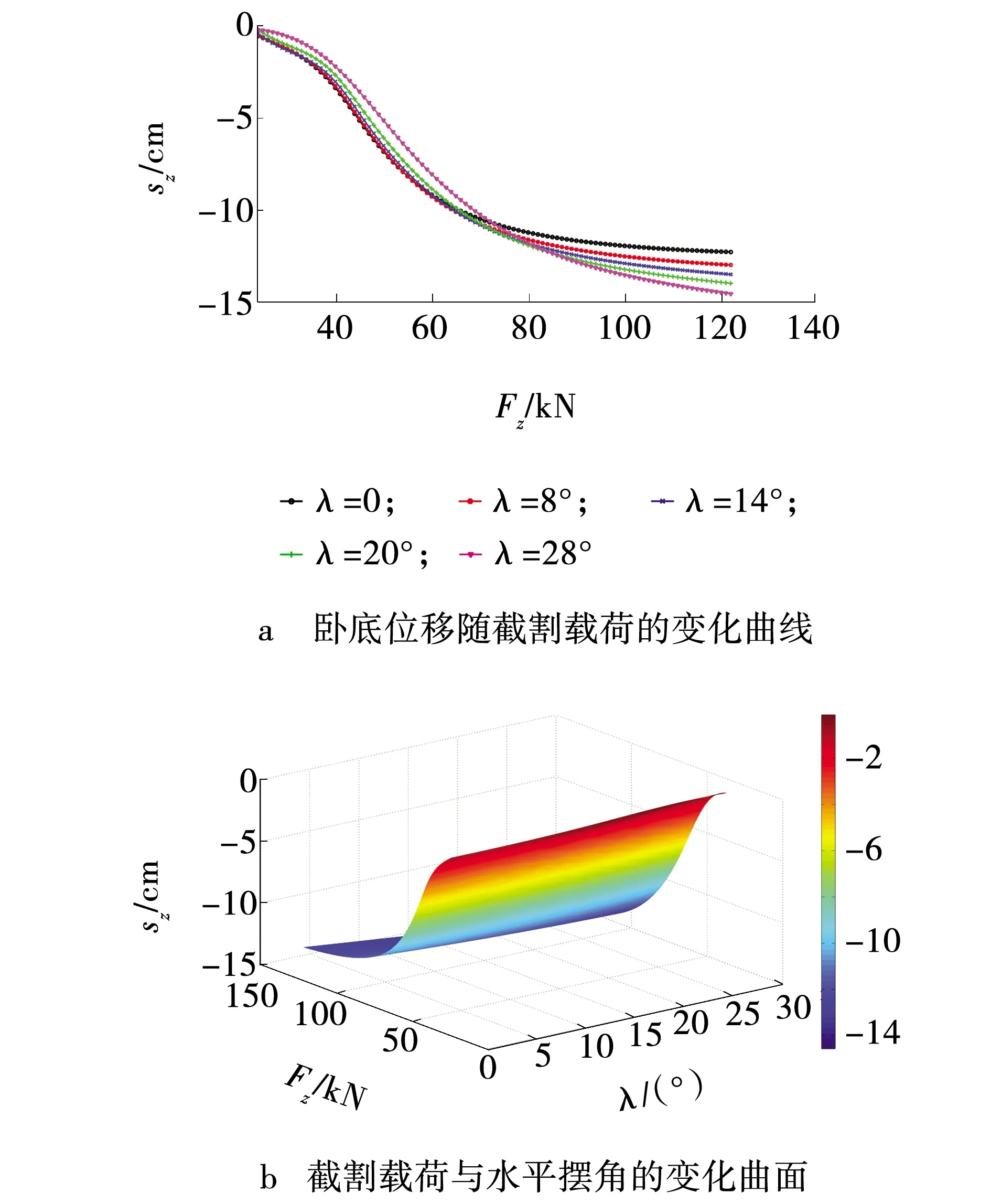
图5 卧底位移响应结果Fig. 5 Response result of floor-based displacement

图6 整机滑移随煤层倾角变化曲线Fig. 6 Relation curve of slippage and dip angle of coal seam

3.2 纵向截割过程

在纵向截割过程中，截割臂垂直摆角不断变化，而水平摆角为一定值。对式(10)～(12)的求解结果进行参数分析，偏向位移、后向位移和卧底位移的响应结果分别如图7～9所示，煤层倾角对整机滑移的影响如图10所示。

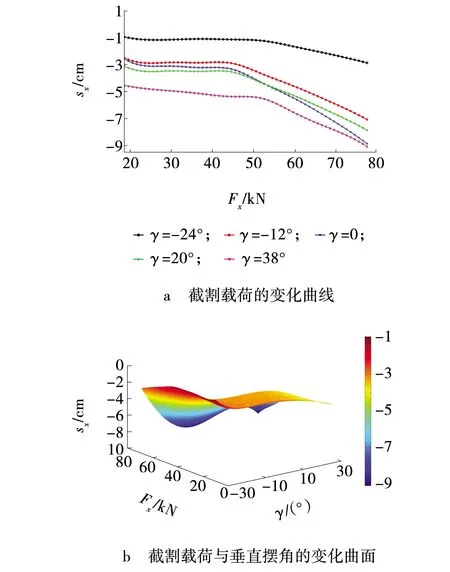
图7 偏向位移响应结果Fig. 7 Response result of lateral displacement

图8 后向位移响应结果Fig. 8 Response result of backward displacement

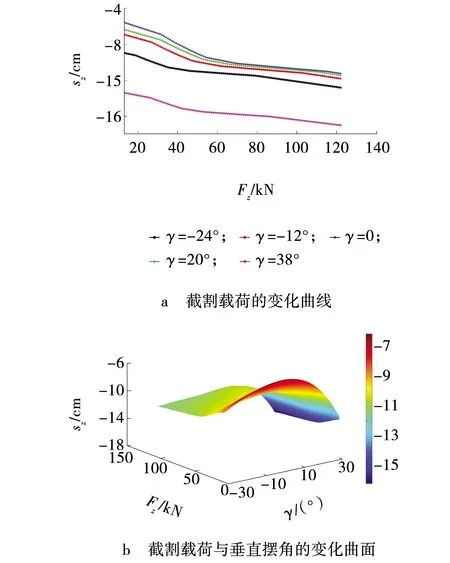
图9 卧底位移响应结果Fig. 9 Response result of floor-based displacement

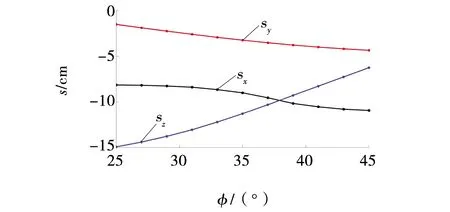
图10 整机滑移随煤层倾角变化曲线Fig. 10 Relation curve of slippage and dip angle of coal seam

在纵向截割过程中，截割载荷对掘进机整机滑移的影响较大，而且截割臂垂直摆角对整机滑移的影响远大于横向截割的情况。在截割载荷的作用下，卧底位移变化最为显著，最大值可达16.9 cm；后向位移变化幅值最小，为4.1 cm；偏向位移的最大值为9 cm。同样地，偏向位移和后向位移随着巷道倾角的增大而增大，卧底位移随着煤层倾角的增大而减小。