强基固本才能厚积薄发——以几道含参绝对值不等式求解为例

郑梦华

江西师范大学数学与信息科学学院 (330022)

掌握数学基础知识是解答数学问题的基础，也是学生数学学习再创造、再发现的基础.绝对值不等式是高中选修内容，而含参绝对值不等式是绝对值不等式的深化与补充.该类题型灵活多变，既考查参数又考查变量，综合性较强;需要学生具有扎实的数学基础知识，也需要学生具有较强的数学能力素养.本文通过几例予以说明.

评注：本题主要考查绝对值基本定义及用定义去绝对值的方法，这是绝对值不等式中最基础的知识和方法，其本质是简化数学问题，强化学生对绝对值本质的理解.

例2 设函数f(x)=|x+1|+|2x-1|,g(x)=|3x-2m|+|3x-4|,若对∀x1∈R,存在x2∈R,使得f(x1)=g(x2)成立，求实数m的取值范围.

解析：由题意，设A={y|y=f(x)},B={y|y=g(x)}，则A⊆B.由f(x)=

评注：求解含参绝对值不等式问题最基本的数学思想方法是分类讨论，本题除考查学生对该思想方法的运用,还考查到绝对值三角不等式的运用，同时,求解中运用的集合思想及数形结合思想也很重要.

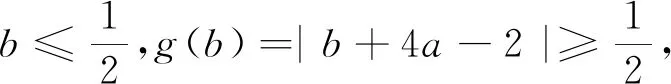
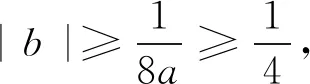
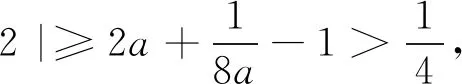
评注：本题涉及三个参变量，并且同时出现“任意”、“存在”两个量词，其本质是一个二次函数的最值问题，但在求解过程中需要运用到分类讨论、数形结合等基本的数学思想方法,同时需要具有代换法及最值函数处理技巧等,其交汇综合性较强.

正如新课标指出的：“数学教育帮助学生掌握现代生活和进一步学习所必需的数学知识、技能、思想和方法；提升学生的数学素养，促进学生思维能力、实践能力和创新意识的发展.”数学问题解决教学应重在强化学生基础知识、基本思想方法训练的基础上，培养学生善于综合运用所学,巧解数学问题.