基于深度学习及UKF 的机器人SLAM*
2020-09-23马国军习朝辉马玉皓王亚军
倪 朋,马国军,习朝辉,马玉皓,王亚军
(1.江苏科技大学电子信息学院,江苏 镇江 212003;2.北方自动控制技术研究所,太原 030006;3.解放军32381 部队,北京 100072)
0 引言
机器人在运动过程中需要利用自身传感器获取周围的环境信息并创建地图,进而确定自己的位置,因此同时定位与建图(Simultaneous Localization and Mapping,SLAM)具有重要的意义。机器人通过“感知-预测-校正”不断更新信息,从而对自身位置的预测更加准确[1]。
卡尔曼滤波以最小线性方差为基础,运用逐步迭代的方式预测状态从而减少噪声影响,但仅适用于线性系统。扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法虽然方法简单易于实现,但是存在计算量大,非线性精度差的缺点[2]。无迹卡尔曼滤波(Unscented Kalman Filter,UKF)采取对函数的概率密度分布求近似的方法,保留高阶项,解决了扩展卡尔曼滤波精度差的缺点[3]。
UKF 是一种非线性动态系统状态估计方法。但是当系统模型存在不确定性时,UKF 的结果会退化甚至发散。文献[4-7]针对这些问题进行了研究。
针对机器人SLAM 中计算复杂、定位精度差、获取地图中路标信息少的问题,考虑到单发多框探测器(Single Shot MultiBox Detector,SSD)可以检测到物体的形状,为此结合SSD 算法进行SLAM 研究。本文在UKF-SLAM 算法的基础上,通过SSD 算法进行目标检测并获取路标信息,然后加入到UKF-SLAM 算法中,提高SLAM 的精度。
1 SSD 目标检测算法
基于深度学习的目标检测是机器人SLAM 的研究方向之一。SSD 作为主要的目标检测框架之一,其无需生成候选框,把目标边框定位转变成回归问题进行解决,是一种直接预测目标类别和边界框的目标检测方法。SSD 通过提取不同尺度图像的特征,减少训练参数量,同时提高准确度和实时性。
为提高检测的效率,SSD 对不同大小的卷积层输出结果进行回归处理,同时改变检测器宽度和高度的比值,从而增加检测目标的种类[8-9]。
1.1 网络结构
SSD 选取VGG16 作为基本框架,在VGG16 框架上增加卷积层以得到更加丰富的特征图进行目标检测。SSD 的网络结构[9]如图1 所示。
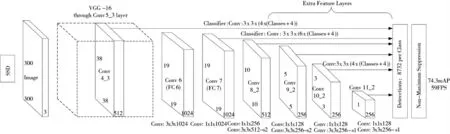
图1 SSD 网络结构
1.2 损失函数
SSD 构建的损失函数与目标搜索框的位置及类别置信度有关,以利于提高优化速度和增加训练结果的稳定性,它是定位损失(locatization loss)与置信度损失(confidence loss)的加权和,表示为
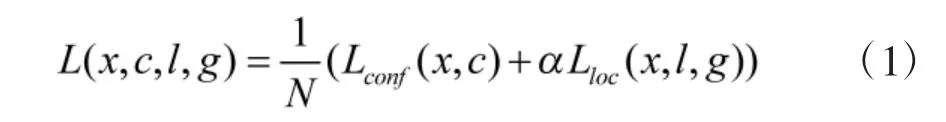
其中,N 为匹配的默认框数量,c 代表置信度,l 是预测框,g 是真实框,x 用来判断预测框和真实框是否匹配,Lconf是置信度损失,Lloc是定位损失,α 为权衡定位损失和置信度损失的加权值。
2 基于UKF 的SLAM 算法
2.1 SLAM 系统模型
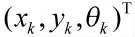
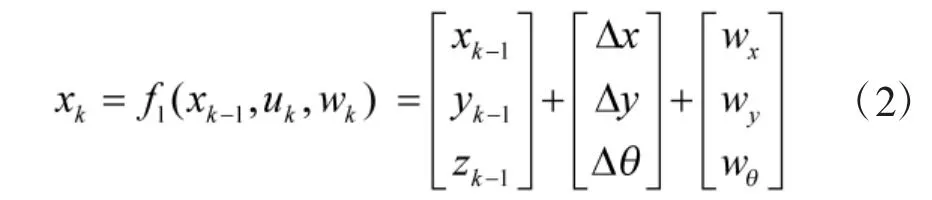
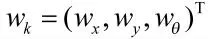
机器人传感器在位置pi处观测到的数据为zk,i,nk,i为观测噪声,则观测方程为
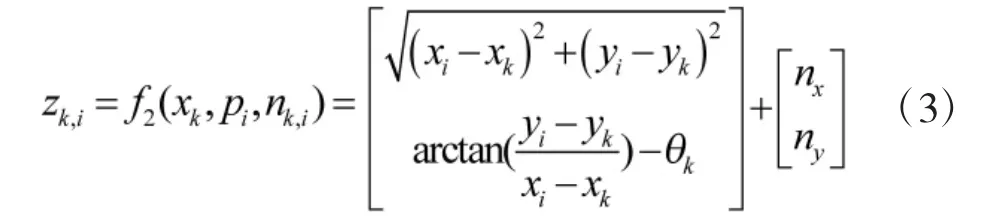
当机器人采用深度相机传感器时,其获取的图像中包含机器人到目标的距离信息,利用SSD 算法检测场景中的目标作为路标信息,最后将路标信息加入到SLAM 算法中,算法总体流程如图2 所示。
2.2 无迹变换
1)计算得到2n+1 个采样点,此处n 为状态的维度;
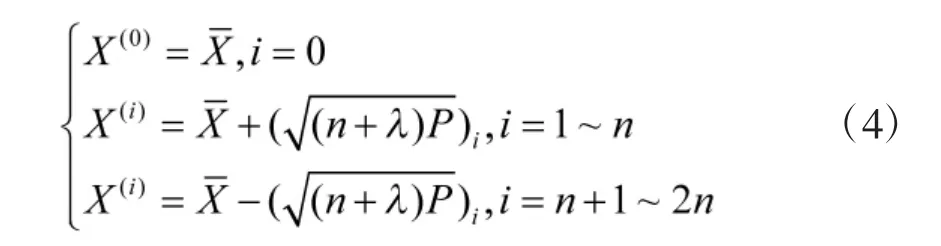
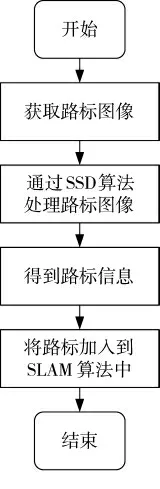
图2 算法流程图
2)计算采样点对应的权值。
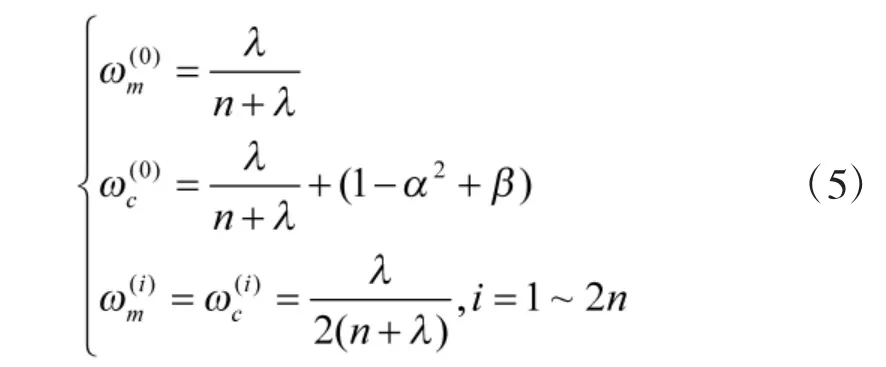
2.3 UKF-SLAM 算法
随机变量X 和观测变量Z 包含的高斯白噪声分别为W(k)和V(k),k 取不同值时,X 和Z 组成的非线性系统为
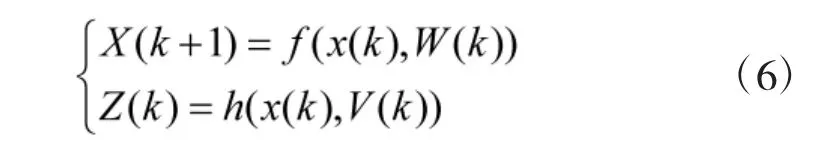
式中,f 代表非线性状态函数,h 代表非线性观测函数[10]。假设W(k)的协方差阵为Q,V(k)的协方差阵为R。随机变量X 的无迹卡尔曼滤波的过程如下所示。
1)根据式(5)和式(6)获取采样点和相应的权值;
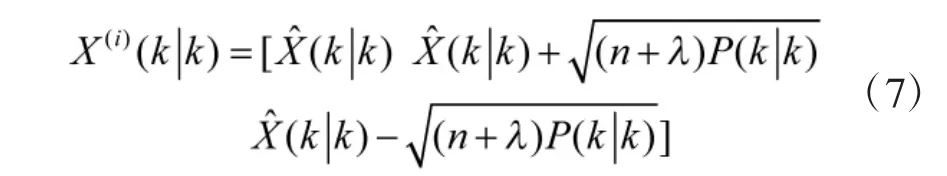
2)计算2n+1 个采样点集合的一步预测结果,i=1,2,…,2n+1;
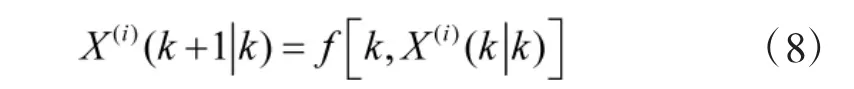
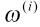
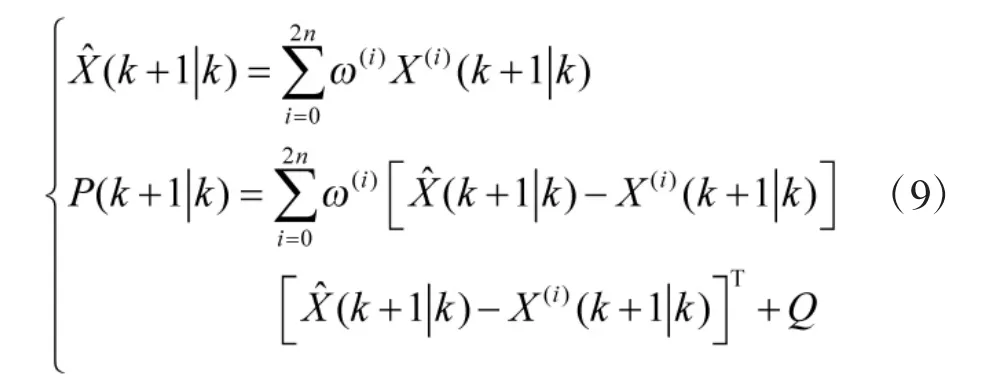
4)由一步预测方程,运用无迹变换,生成新的采样点集合;
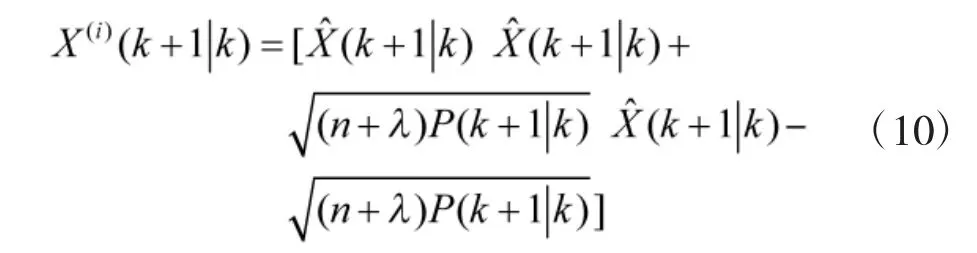
5)根据预测的采样点集合的观测方程,得出预测的观测值,i=1,2,…,2n+1;
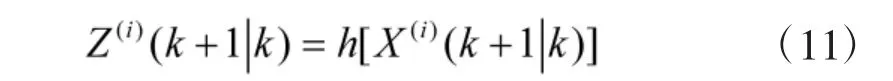
6)根据得出的采样点集合的预测结果,由加权求和可得系统预测的均值和协方差;
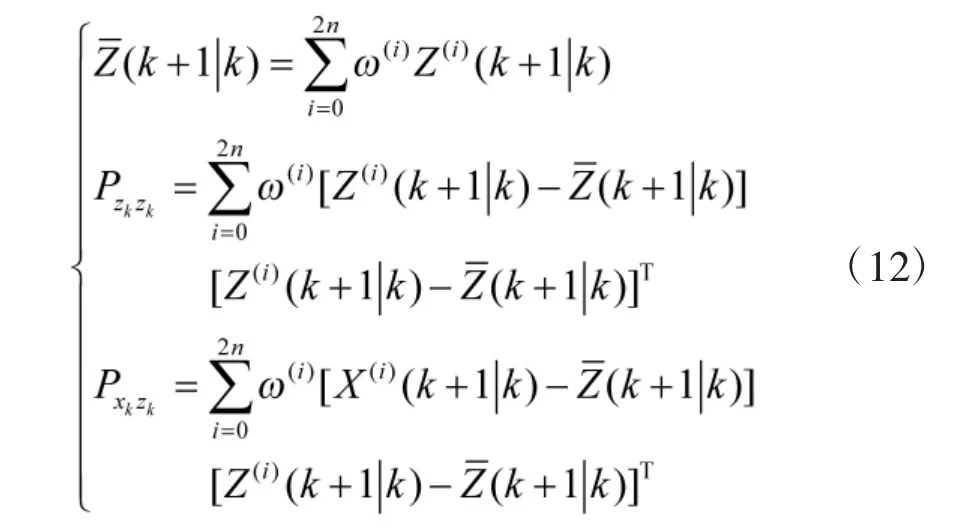
7)计算得到卡尔曼增益矩阵;
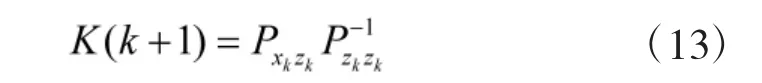
8)求解得到系统的状态更新以及协方差更新。
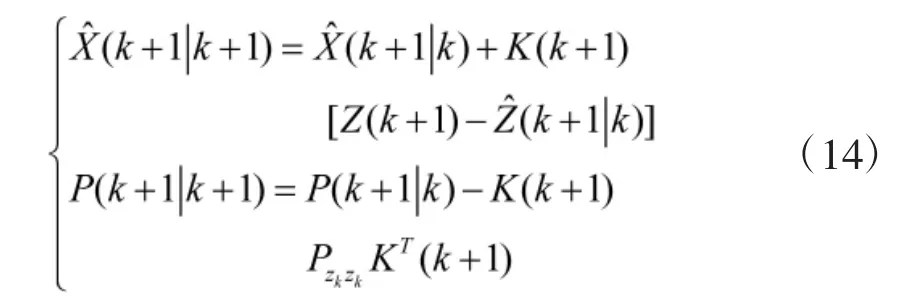
3 实验结果与分析
3.1 实验环境
本文使用Intel Realsense D435i 深度相机,实物如图3 所示,尺寸为90 mm×25 mm×25 mm,并且搭载了惯性传感单元(Inertial Measurement Unit,IMU)。Intel Realsense D435i 采用结构光技术,可以直接得到相机到目标物体的距离。

图3 Inter Realsense D435i 深度相机
实验场景和示意图分别如图4 和图5 所示,4个路标分别为“瓶”、“椅子”、“宠物猫”、“宠物鸟”。实验过程中,利用深度相机获取路标的信息,以靠近墙面的起始点为原点,选取宽200 cm,长500 cm的区域进行实验。

图4 实验场景图
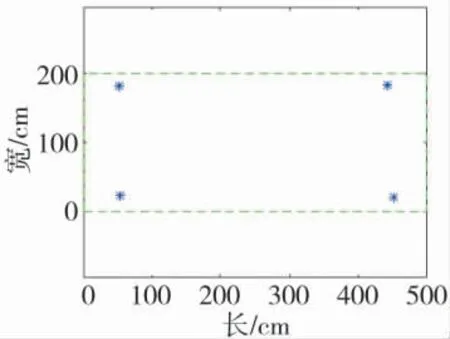
图5 实验示意图
3.2 实验数据及结果分析
由Realsense D435i 相机获取的深度图像需要经过配准,以生成配准深度图像。通过配准,将深度图和彩色图对齐,结果如图6 所示。

图6 彩色图和深度图配准后的结果
利用SSD 模型来检测场景中的目标。由于彩色图和深度图已经配准对齐,可以将彩色图检测到的边界框投影到深度图,如图7 所示。对其中的深度数据求平均值,得到相机到目标距离,进而得到路标的位置坐标。
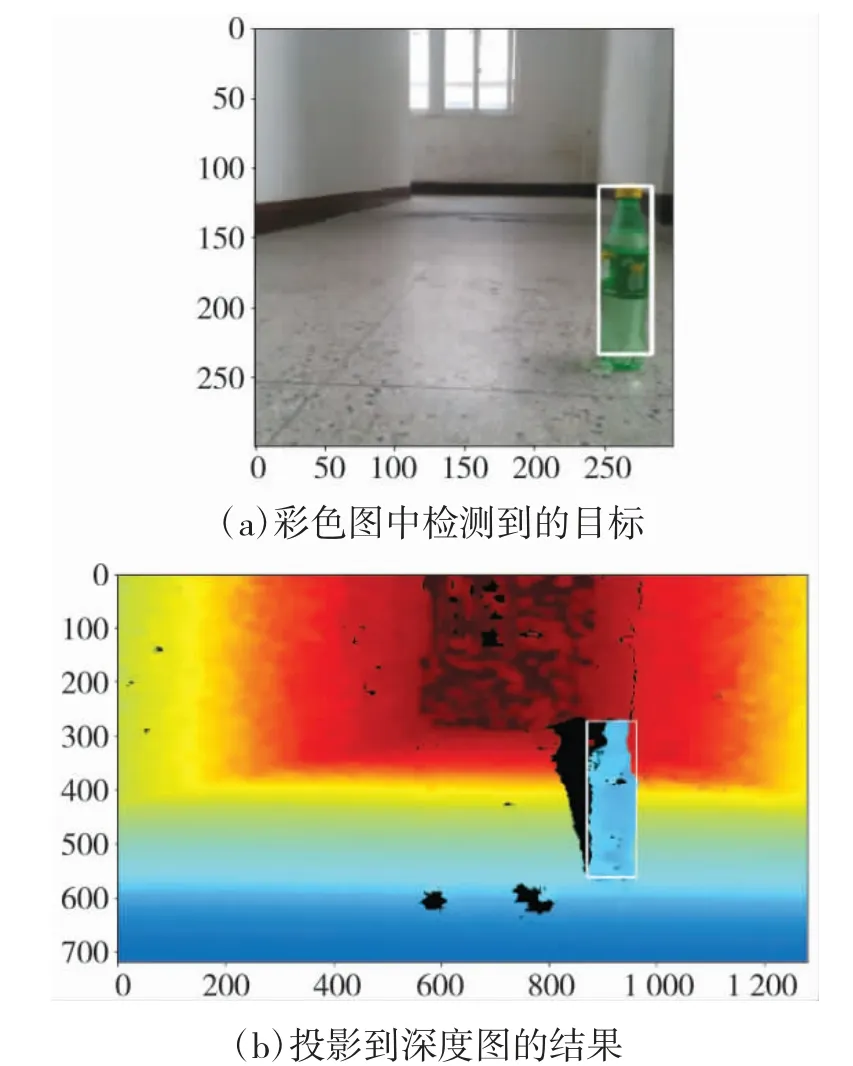
图7 瓶的检测结果
测量得到瓶的坐标为(53,23),单位为厘米。然后,对路标“椅子”、“宠物猫”、“宠物鸟”进行测量,坐标分别为(452,20),(443,185),(52,182)。
根据测量得到的数据,分别以EKF-SLAM 和UKF-SLAM 算法为基础进行仿真。设机器人初始位姿为(0,0),沿设定的路径逆时针移动。速度为3 cm/s,附加零均值且方差为0.1 的高斯噪声,系统协方差初始化为0。仿真结果如图8 所示,其中“*”表示路标点,虚线表示真实的轨迹,实线表示估计的结果。
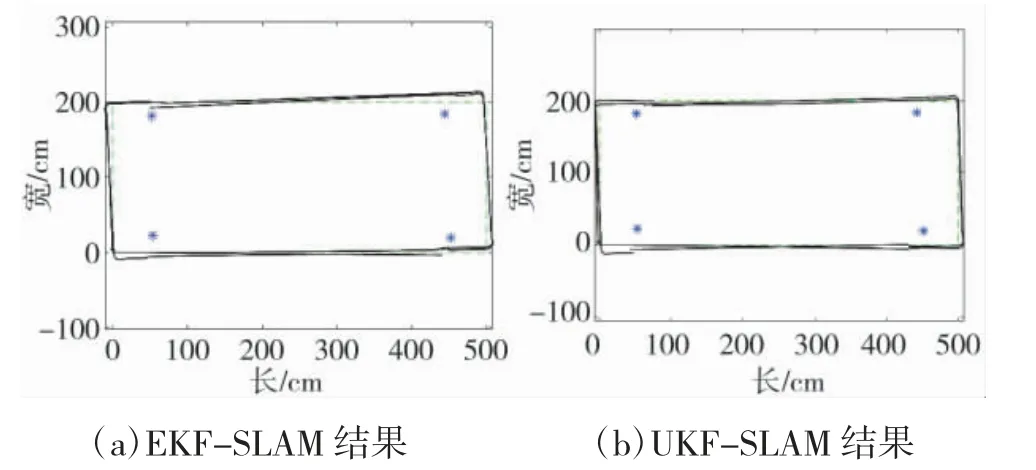
图8 SLAM 结果图
为评估算法精度,分别计算X 轴和Y 轴方向的误差,对比EKF-SLAM 算法和UKF-SLAM 算法的精度,结果如图9 所示。虚线为EKF-SLAM 的误差,实线为UKF-SLAM 的误差。
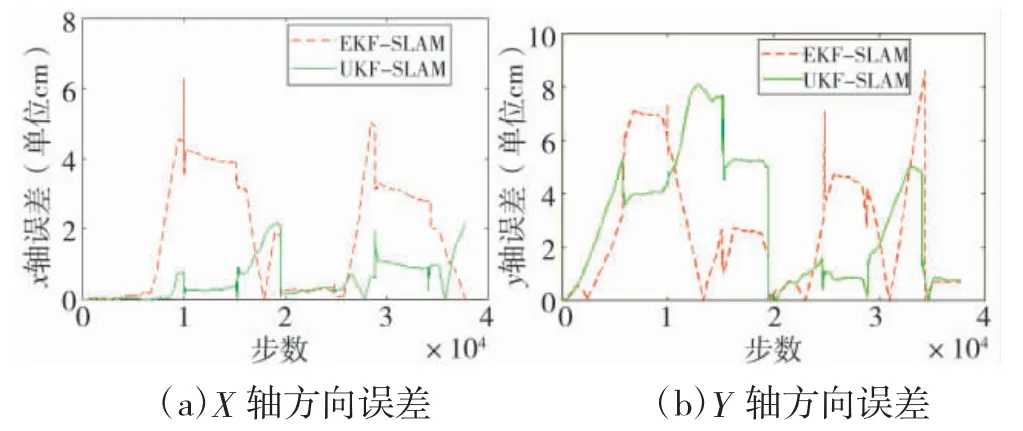
图9 误差结果图
由图9 可以看出UKF-SLAM 的误差小于EKF-SLAM。分别计算X 轴方向和Y 轴方向的平均误差,如表1 所示。
由表1 可知,对于EKF-SLAM 算法,X 轴方向的平均误差为1.81 cm,Y 轴方向的平均误差为3.07 cm;对于UKF-SLAM 算法,X 轴方向的平均误差为0.55 cm,Y 轴方向的平均误差为2.68 cm。总体来说,UKF-SLAM 的误差小于EKF-SLAM 的误差。

表1 算法结果对比
4 结论
本文提出融合深度学习和UKF 的机器人SLAM 方法,通过Intel Realsense D435i 深度相机获取彩色图和深度图,并将彩色图和深度图进行配准;利用深度学习SSD 算法获取路标坐标并加入到UKF-SLAM 算法中,提高了SLAM 的精度。
随着人工智能技术的发展,今后将通过研究轻量化的深度学习及SLAM 方法,以提高移动机器人获取路标的速度和准确度,进一步提升SLAM的效率。
