一种基于混合算法的火力规划方法
2020-09-23浦方韬
沈 驰,浦方韬
(中国电子科技集团第二十八研究所,南京 210007)
0 引言
火力规划是根据作战任务,战场态势以及武器装备毁伤能力,按照一定的分配规则,将敌方目标分配给我方火力单元的过程。战前与战时的火力规划可以有效提高我方火力单元的打击效率,节约火力资源,对作战效果有重要影响。
火力规划问题已被证明是NP-hard 问题,其求解难度随着问题复杂程度的增大呈指数上升。目前,国内外对于这类问题的求解主要采用云遗传算法[1]、蚁群算法[2]、多样性粒子群算法[3]、离散粒子群算法[4]、量子免疫克隆算法[5]以及禁忌搜索算法[6]等。遗传算法是由美国Michigan 大学的John Holland 教授根据生物进化中的信息遗传与自然选择机制提出的一种优化算法。遗传算法具有较好的全局搜索能力,但存在进化较慢,易早熟收敛的问题。并且,随着约束条件的加入和问题复杂程度的增大,遗传算法的搜索效率不断降低。
采用遗传算法进行火力规划存在两个主要问题,一是火力规划问题具有多个约束条件,对于约束条件的处理,文献[7]提出了采用惩罚函数的方法,文献[8]提出了对子代个体进行合法性判断的方法。二是当火力规划问题涉及的火力单元与目标数量较多,问题较为复杂时,遗传算法搜索效率较低,文献[9-10]提出了加快收敛的方式,但在火力规划问题中适用性不强。因此,需探寻一种改进算法以解决上述问题。
本文提出了一种基于贪心策略和改进遗传算法的混合算法,通过编码方式和自体杂交算子处理约束条件,将贪心策略应用于种群的初始化过程和一定复杂程度以上问题的求解。本文提出的混合算法针对不同复杂程度的火力规划问题均有较好的寻优能力,并大大减少了算法的运行时间。
1 火力规划问题描述
现代战争中,战前规划在大规模战斗中扮演了重要角色,根据战前的情报信息,我方对敌方各目标进行毁伤分析,获得我方各火力单元摧毁该目标所需要的弹药种类与数量。通过战前火力规划形成打击方案,将敌方各目标分配给我方火力单元实施打击任务,明确我方火力单元达成预期毁伤任务所需的弹药种类与数量,为我方弹药保障提供支持。
本文讨论的火力规划问题,是大规模作战的战前火力规划过程,对于作战进程中因我方火力单元被摧毁而产生的重新规划及火力转移等问题可通过分(群)队级的临机规划解决,因此,在文中不作具体讨论。
现假设我方火力单元数量为M,已探测到敌方目标数量为N,敌方目标数量大于我方火力单元数量(N>M),定义此火力规划问题的复杂程度为M*N。要求将敌方目标合理分配给我方火力单元,每个火力单元对各目标完成预定打击任务所需消耗的弹药数量为Ci,要求完成打击任务所需火力资源最少,即

式中,T 为目标函数。此外,火力规划问题还需满足以下3 个约束条件:
1)每个目标仅由一个火力单元实施打击任务;
3)火力单元完成打击任务所需的弹药数量不能超过该火力单元可携行弹药总量。
2 基于贪心策略和改进遗传算法的混合算法的实现
2.1 贪心策略
通过某种算法可以求出火力单元对各目标完成既定打击任务所需消耗的弹药数量,这些数据可以组成一个M*N 的矩阵P,矩阵元素Pij表示第i个火力单元对第j 个目标实施打击所消耗的弹药数量。
在最优分配方案中,矩阵P 的每一列有且仅有一个Pij被选中,且被选中的Pij为该列最小或较小值,因此,引入贪心策略来进行快速选择。具体步骤为:
1)随机选取第j(j∈[1,N])列为起始列,选取第j 列的最小值;
2)从第j 列向后,逐列选取符合约束条件的该列最小值;
3)从第j 列向前,逐列选取符合约束条件的该列最小值。
2.2 编码
在相似问题的求解中,文献[11]提出二进制编码方式,文献[12-13]提出整数编码方式,但在杂交与变异过程中,这两种编码方式均会破坏所有3 个约束条件。因此,为解决破坏约束条件的问题,提出一种编码方式:染色体表示为与矩阵P 大小一致的分配矩阵Q,其中Qij表示第i 个火力单元对第j 个目标的打击状态,采用二进制编码,1 为打击,0 为不打击。矩阵中每个元素为一个基因,每一行为一个基因组。
2.3 适应度函数
要求以最少火力资源消耗完成既定打击任务。因此,选择式(1)中目标函数作为适应度函数,即

2.4 种群初始化
遗传算法中常随机生成一定数量的合法染色体作为初始种群。当问题复杂程度增大时,采用随机初始化的遗传算法收敛速度减缓,无法保证在一定代数内收敛。由2.1 中分析可知,采用贪心策略产生的个体均为适应度较为优秀的个体,因此,初始种群的部分染色体采用贪心策略产生以加快算法收敛速度,剩余染色体随机生成来维持初始种群的多样性。
2.5 自体杂交算子
采用2.2 中定义的染色体,当两个染色体随机交换某个基因或基因组时,都可能破坏所有约束条件。因此,本文提出自体杂交算子以减少破坏约束的数量。
自体杂交算子在进行杂交操作时,随机交换染色体的任意两个基因组。因父代染色体为合法染色体,所以交换之后的染色体不会破坏约束1)与约束2),仅可能破坏约束3),即携行弹药总量不足以完成交换之后的打击任务,大大提高了子代中合法染色体的比例。
采用自体杂交算子,无法通过不同染色体之间基因交换获得其他染色体中的优良基因,使得基因多样性减少。本算法通过提高变异几率来丰富基因的多样性。
2.6 选择算子
选择算子分为两步,首先从目标种群中选择适应度最优的个体,再采用轮盘赌的方式,在除去最优适应度个体的种群中选择若干个体,与最优适应度个体一起构成选择结果。
2.7 变异算子
变异算子采用两点变异,首先随机选择一个基因,若此基因的值为1,则重新选择;若此基因的值为0,且该火力单元被分配的目标数量未达上限,则将此基因的值置为1,并且假设这个基因位于第j列,将第j 列另一个值为1 的基因置为0,完成变异操作。
2.8 合法性校验
自体杂交算子和变异算子经过改进,在执行的过程中,对于杂交或变异后的个体,检查发生变化的两个基因组是否满足约束3)的条件,若满足,子代个体合法,通过校验;若不满足,对父代个体重新执行相应算子,直至通过校验。
2.9 算法描述及复杂度
混合算法求解火力规划问题可分为两个主要步骤:计算问题复杂程度;根据复杂程度的大小选择采用贪心算法或改进遗传算法进行求解。
步骤0 根据我方火力单元数量M 和敌方目标数量N 计算火力规划问题复杂程度,当复杂程度大于阈值Th 时,采用贪心算法求解,否则采用改进遗传算法求解。
2.9.1 贪心算法
步骤1 将矩阵P 中的随机k 列作为起始列采用贪心策略得到k 个分配方案。步骤1 的复杂度为O(kMN)。
步骤2 取k 个分配方案中适应度值最优的为火力规划的结果。步骤2 的复杂度为O(kMN)。
贪心算法考虑参数的复杂度为O(kMN)。
2.9.2 改进遗传算法
步骤1 设置参数。设置以下参数:种群数量p,子种群大小c,变异概率m 和最大进化代数max_iter。
步骤2 编码及种群初始化。采用2.2 中的编码方式。初始种群的产生分为以下两种情况:当敌方目标数量少于p/2 时,以每一列为起始列采用贪心策略得到N 个染色体,剩余染色体通过随机的方式产生。当敌方目标数量大于p/2 时,以随机选取的p/2 列作为起始列采用贪心策略得到p/2 个染色体,剩余p/2 个染色体通过随机的方式产生。步骤2 的复杂度为O(pMN)。
步骤3 选择。从父代种群中选择包括最优适应度个体在内的共p/5 个个体。步骤3 的复杂度为O(pMN+p)。
步骤4 自体杂交。对步骤3 中选出的每一个个体执行c 次自体杂交操作形成一个子种群,共形成p/5 个子种群。最优适应度个体的子种群中包含最优适应度个体本身。步骤4 的复杂度为O(2pc/5)。
步骤5 选择。从步骤4 产生的每个子种群中选择5 个个体进入下一代种群,共选出p 个个体。步骤5 的复杂度为O(pcMN/5+pc/5)。
步骤6 变异。对步骤5 产生的下一代种群中除最优适应度个体之外的所有个体按照变异概率m执行变异操作。经过变异后种群完成一次进化,进化次数加一。步骤6 的复杂度为O(3p)。
步骤7 判断算法终止条件。若种群达到最大进化代数,算法终止,输出末代种群最优适应度个体为最优解,否则转步骤3。步骤7 的复杂度为O(1)。
改进遗传算法考虑参数的复杂度为O(pMN+max_iter*(p*(MN+4)+pc*(MN+3)/5)。
2.10 误差时间系数
为确定阈值Th 的取值,定义误差时间系数et来比较贪心算法与改进遗传算法的综合效能,误差时间系数定义为
et=err×comp
其中,err 为相对误差,定义为贪心算法相对改进遗传算法的误差,具体为

式中,errg为贪心算法最优个体适应度,erri为改进遗传算法最优个体适应度。
comp 为相对算法复杂度,定义为贪心算法复杂度与改进遗传算法复杂度之比,具体为
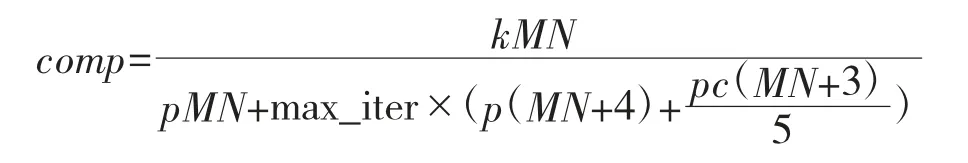
算法复杂度越低,其运行时间越短,因此,et 的值综合反映了算法误差与运行时间的效能,et 的值越小,则贪心算法综合效能越好。
3 仿真与分析
混合算法主要用于求解复杂程度较大的火力规划问题,为验证混合算法的有效性,通过实验获得了误差时间系数随问题复杂程度变化的图像,以此进行阈值Th 的选取;通过两个不同复杂程度的火力规划问题的仿真,对比了采用不同的种群初始化方法的改进遗传算法以及贪心算法的结果。
火力规划问题仿真所需弹药消耗矩阵P,暂无数据可以参考,因此,根据火力单元与目标所固有的杀伤能力与防护能力精心设计了弹药消耗矩阵P,其每行元素由随机数发生器产生,随机数的范围由该行的索引确定。
混合算法的参数设置如下:贪心算法k=100,种群数量p=50,子种群大小c=20,变异概率m=0.2,最大进化代数max_iter=100。
3.1 误差时间系数分析
为获得误差时间系数随问题复杂程度变化的图像,对25 个复杂程度介于50 和60 000 之间的火力规划问题进行了仿真,对每一个问题,取10 次仿真的相对误差平均值作为该复杂程度的相对误差,再通过相对误差求得该复杂程度下的误差时间系数。因复杂程度区间较大,图像的x 轴为复杂程度的自然对数。
图1 为误差随复杂程度变化的图像,图2 为误差时间系数随复杂程度变化的图像。
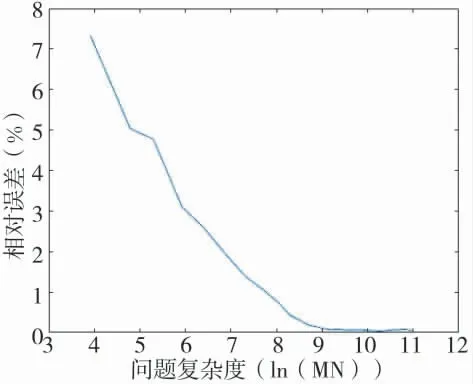
图1 相对误差随问题复杂程度变化曲线

图2 误差时间系数随问题复杂程度变化曲线
通过仿真可知,相对误差及误差时间系数均随着问题复杂程度的增大而减小,表明当火力规划问题越来越复杂时,贪心算法的综合效能越来越好,在这种情况下,阈值Th 可综合考虑实际应用中的硬件条件以及对误差的容忍度进行选取,给予了作战筹划人员较大的自主选择权。在本文的仿真中,取误差为1%时的复杂程度作为阈值Th,取值约为2 300。
3.2 不同复杂程度问题的仿真与对比
3.2.1 复杂程度小于阈值Th
选取我方火力单元数量M=25,敌方目标数量N=50,问题复杂程度为1 250,小于阈值Th。分别采用完全随机初始化与贪心策略的初始化的混合算法的收敛曲线如图3 所示。

图3 复杂程度小于阈值的算法收敛曲线
由图3 可知,采用贪心策略进行初始化的种群的最优个体适应度较优,可以加快算法收敛速度,并可以取得相对贪心算法更好的结果,采用完全随机初始化的算法在此复杂程度下可在100 代内收敛,但其最优个体的适应度较差,算法陷入局部最优。
3.2.2 复杂程度大于阈值Th
选取我方火力单元数量M=40,敌方目标数量N=80,问题复杂程度为3 200,大于阈值Th。初始化方式仍采用前述两种方式,收敛曲线如图4 所示。
由图4 可知,当复杂程度大于阈值时,采用完全随机初始化的算法已无法在100 代内收敛,采用贪心策略初始化的算法虽然可以收敛,但初始种群最优适应度与末代种群最优适应度相差较小,搜索效率较低,且贪心算法所得结果与末代种群最优适应度误差极小。此时采用贪婪算法,可以大大提高求解速度,满足实时性的要求,证明了混合算法可以有效平衡误差与求解时间,是解决复杂火力规划问题的有效途径。
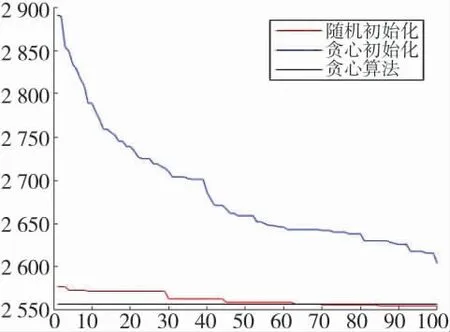
图4 复杂程度大于阈值的算法收敛曲线
4 结论
本文针对火力规划问题,提出了一种适用于不同复杂程度问题的采用贪心策略与改进遗传算法的混合算法,并通过仿真实验得到以下结论:
1)采用自体杂交算子和改进的两点变异算子可以大大提高杂交与变异操作产生的子代中合法染色体的比例,从而提高搜索效率,加快算法运行时间。
2)采用贪心策略对种群进行初始化可以大大加快种群的收敛速度并可在一定代数内获得更加优秀的解。
3)混合算法可以有效平衡时间成本与解的质量,通过结合实际需求合理选择阈值的大小,使各种复杂程度的问题都可在一定时间内获得较为满意的解。
