火炮制退机节制杆稳健优化设计方法研究*

2020-09-23罗中峰管小荣

火力与指挥控制 2020年8期

罗中峰，管小荣，徐诚

（南京理工大学机械工程学院，南京 210094）

0 引言

在反后坐装置其他参数不变的前提下，调整节制杆结构参数既可以保证后坐性能，又可以改善炮身受力状况。在过去的十几年里，学者们一直致力于火炮节制杆优化方面的研究。谈乐斌等［1］基于“设计-评价-再设计”的原则，通过手动改变参数的方法进行了节制杆的优化。宗士增等［2］基于以最大后坐阻力最小为目标，最大后坐长为约束，节制杆各圆锥段直径为设计变量的节制杆优化模型对某节制杆进行了数值优化。洪亚军等［3］在节制杆优化过程中综合考虑了身管和装药参数等对后坐性能的影响。为了得到节制杆结构参数的公差带，李荣等［4］将节制杆结构参数的公差带分解为3 个独立参数带入到节制杆优化模型，并建立了一套基于非支配排序遗传算法和对称拉丁超立方试验方法的寻优策略。张晓东等［5］建立了基于准两相流内弹道方程的炮膛合力计算模型，并提供了一种利用Godunov 差分格式计算炮膛合力的数值方法。上述研究存在以下两个问题：没有充分考虑坡膛和膛线对炮膛合力的影响；没有考虑节制杆参数在公差带内的分布情况。本文将针对以上问题展开相关的研究。

1 节制杆优化模型

本文以带沟槽式复进节制器的节制杆式制退机和液体气压式复进机组成的反后坐装置为例进行相关研究。

1.1 后坐运动微分方程

取后坐部分为研究对象，建立如式（1）所示后坐运动微分方程［6］。

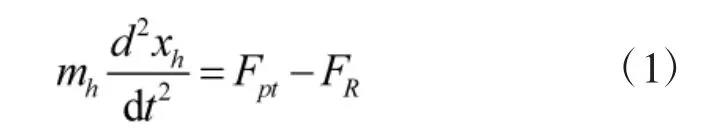
1.1.1 炮膛合力

根据定义，炮膛合力（Fpt）可以按式（2）进行计算。

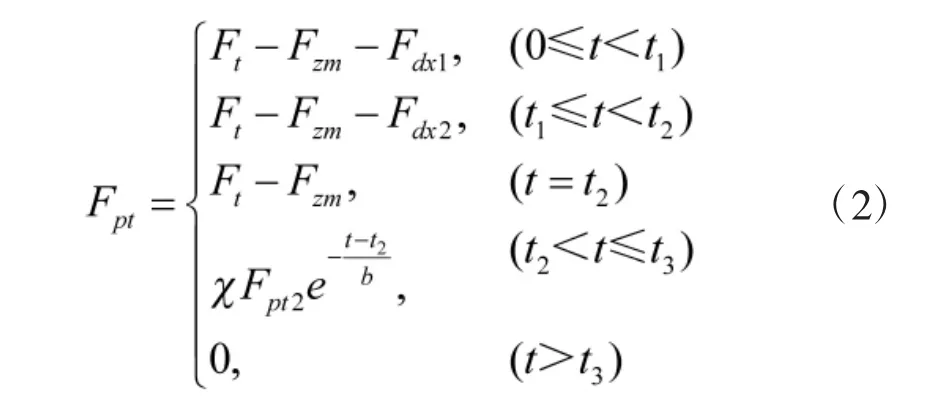
1）弹丸对坡膛的轴向分力和弹丸对膛线的轴向分力

弹丸对坡膛轴向分力（Fdx1）可以按式（3）进行计算。

其中

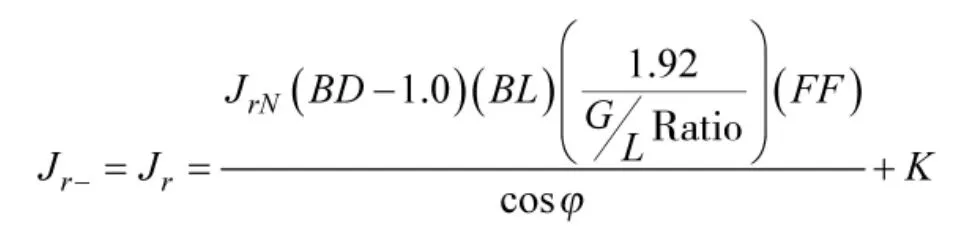
坡膛对弹丸的标准轴向抵制压强（JrN）是弹丸行程的函数（如表1［7］所示）。

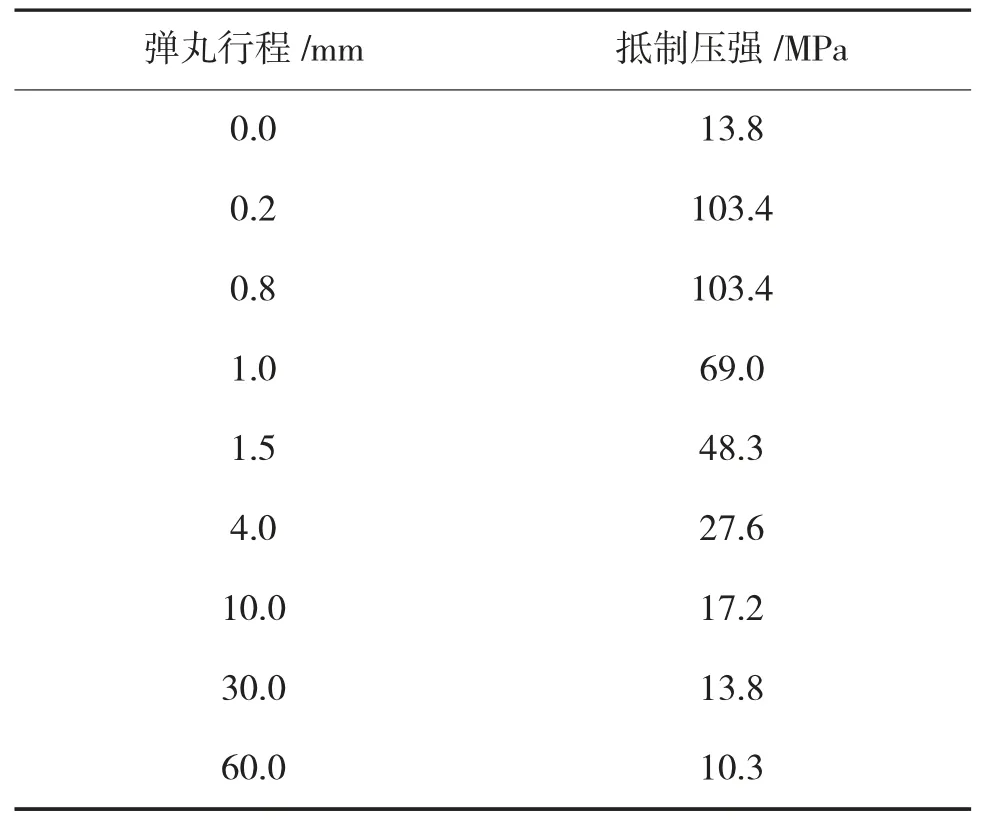
表1 坡膛对弹丸的标准轴向抵制压强对应表

弹丸对膛线的轴向分力（Fdx2）可以按式（4）进行计算。

其中

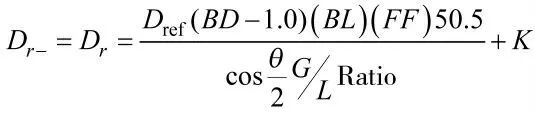
式中，参考抵制压强（Dref）可以根据挤进过程完成前后抵制压强的连续性求得。

2）火药燃气作用在膛底的轴向分力和火药燃气作用在药室锥面上的轴向分力

为了充分考虑坡膛和膛线对内弹道过程的影响，基于前面计算得到的坡膛和膛线对弹丸的轴向抵制压强和Bear-Franke 内弹道方程［8］，火药燃气作用在膛底轴向分力（Ft）和药室锥面上的轴向分力（Fzm）可以按照式（5）进行计算。式（5）中所需火药燃烧方程可参考经典内弹道方程。

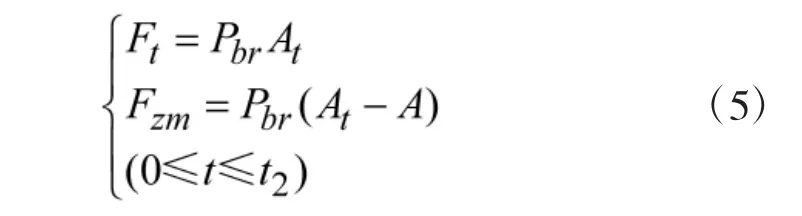
其中

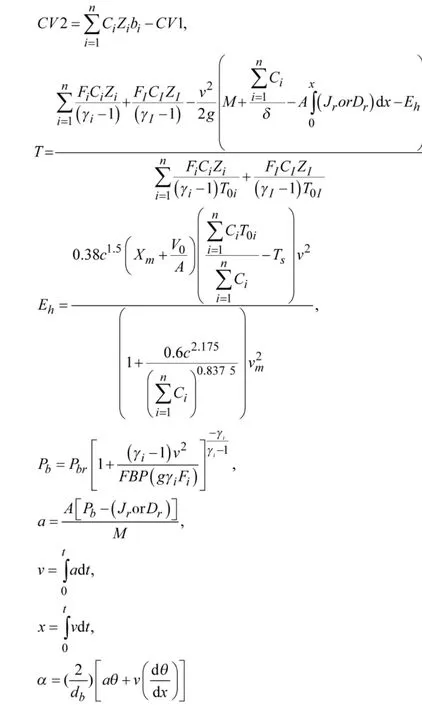
1.1.2 后坐阻力

后坐阻力可根据式（6）［6］进行计算。

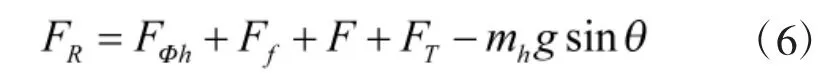
其中

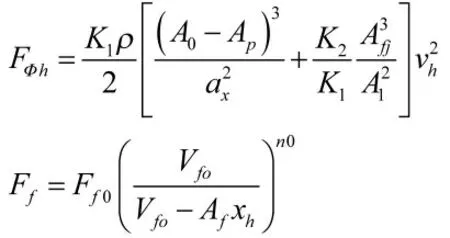
1.1.3 模型验证

在表2 所示条件下的试验和计算后坐阻力如图1 所示。从图1 可知，试验和计算后坐阻力很相近。所以可以基于上述模型进行后坐过程的计算。

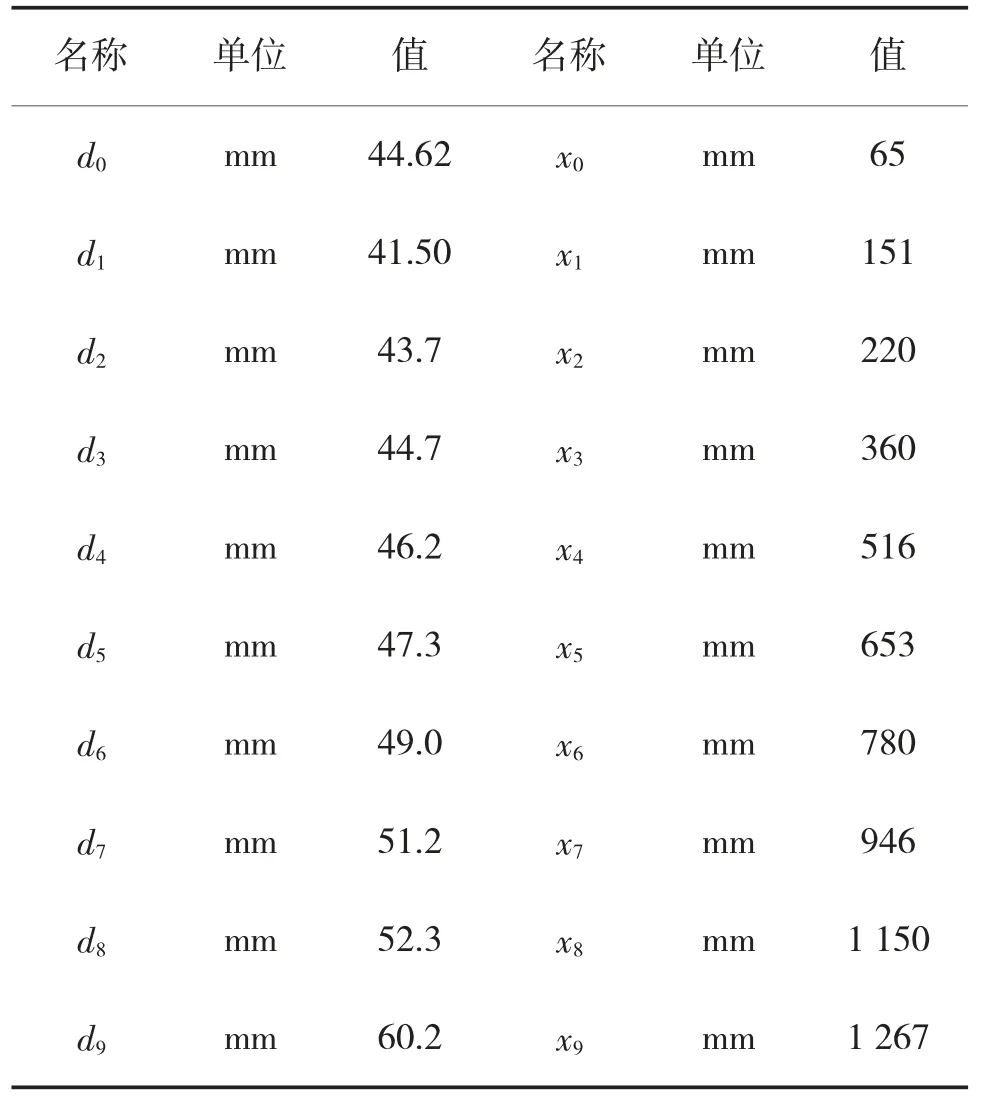
表2 试验和计算条件

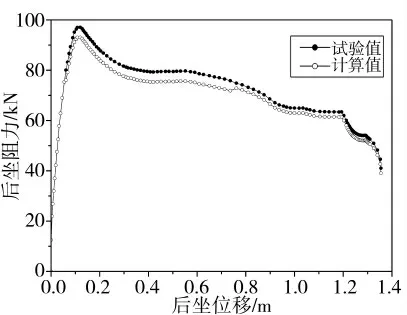
图1 后坐阻力对比图

1.2 节制杆优化模型

下面将在最大射程角条件下建立节制杆优化模型。

1.2.1 目标函数

第1 个优化目标是最大后坐阻力最小，即：

第2 个优化目标是后坐长度最小，即：

1.2.2 约束

根据节制杆稳定性要求，节制杆各折点处的直径必须大于或等于节制杆最小界面直径。同时为了使节制杆能够顺利通过节制环，节制杆各段折点处的直径必须小于节制环最小直径。其次为了保证后坐性能，还需将最大后坐阻力和后坐长度控制在一定的范围内。

1.2.3 设计变量

选节制杆各段折点处的轴向长度（x0，x1，x2，…，xn）和节制杆各段折点处的直径（d0，d1，d2，…，dn）为设计变量。

2 稳健优化方法

根据节制杆优化模型多目标多约束的特点，本节将给出一种基于全局灵敏度分析技术的现代稳健优化设计方法。

2.1 建立优化模型

根据优化目的，建立如式（9）所示优化模型。

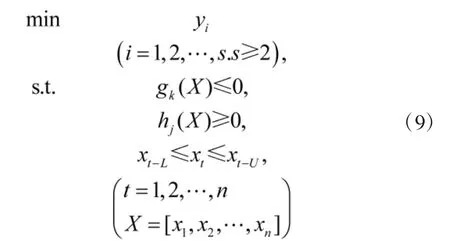
基于节制杆优化模型的特点，上述优化模型只考虑了一类优化目标（最小），两类约束（gk（X）和hj（X））。

2.2 改进优化模型

为了保证优化模型的解都是稳健的，需要对上述优化模型进行适当改进。改进的方法是加大约束和设计变量与其边界的距离。结果如式（10）所示。）

2.3 稳健优化起点

先对改进模型进行优化求解，获得其Pareto 解集；然后再对获得的Pareto 解集中的解进行比较，选出最优Pareto 解作为稳健优化起点。下面是最优Pareto 解的确定方法。假设改进模型的Pareto 解集如下：

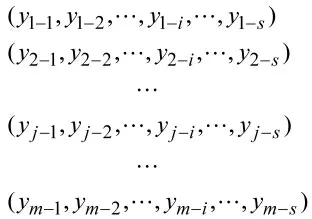
为了便于比较，首先将各个Pareto 解按式（11）进行转换。

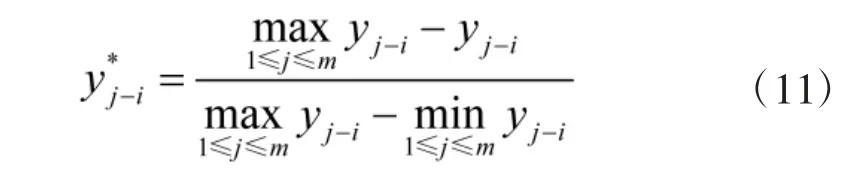
式（11）以第j 个Pareto 解中第i 个优化目标的实际值与Pareto 解集中第i 个优化目标的最大值之间的距离为依据进行转换：如果第j 个Pareto 解中第i 个优化目标的实际值与其对应的最大值相等，则其转换值为0；如果第j 个Pareto 解中第i 个优化目标的实际值距其对应的最大值最远，则其转换值为1；其他情况，则转换值介于0 与1 之间。基于上述规则，改进模型的Pareto 解集转化结果如下所示：

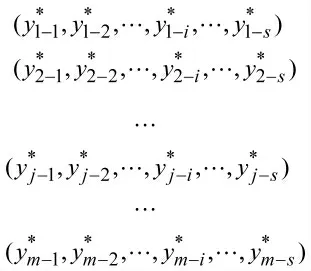
第j 组Pareto 解的评分为：

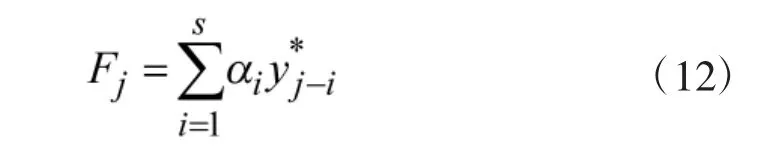
评分最高的Pareto 解就是最优Pareto 解。

2.4 变量分布确定

以设计变量xt为例，如果节制杆的加工工艺水平高，xt服从正态分布；如果节制杆的加工工艺水平一般，xt服从均匀分布。当xt服从正态分布时，以稳健优化起点为期望，dt2/9 为方差。当设计变量服从均匀分布时，以稳健优化起点为期望，dt2/3 为方差。

2.5 单目标稳健优化

在进行单目标的稳健优化前，需要先将多目标的改进优化模型根据优化目标分解为若干个单目标的子优化模型。其中第i 个优化子模型如式（13）所示。

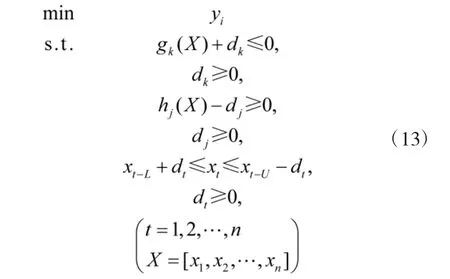
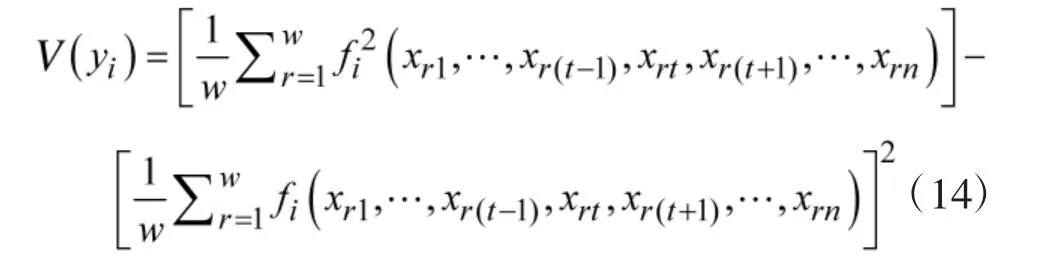
下面以第i 个优化子模型为例，对单个优化目标的稳健优化流程进行说明。首先计算第i 个优化目标和约束的方差。第i 个优化目标方差可以依据式（14）［9］计算。式（14）中设计变量的样本可根据蒙特卡洛法或半蒙特卡洛法，基于上述已经确定的变量分布产生。参照式（14），可以计算约束gk（X）的方差（V（gk（X）））和约束hj（X）的方差（V（hj（X）））。

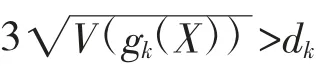
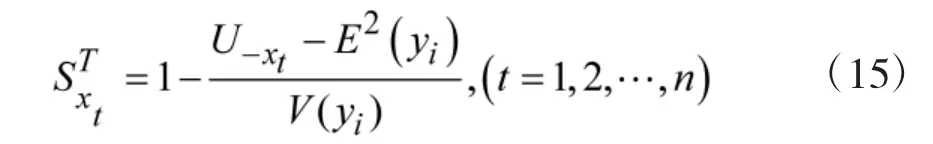
其中

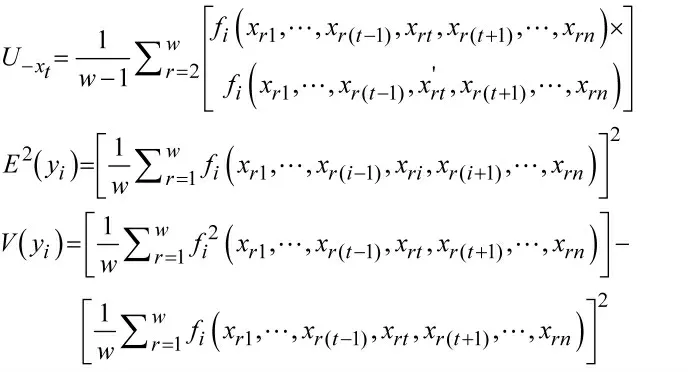
确定所有调整对象后，进行对应的调整，并依据设计变量最新的分布重新计算优化目标和约束的方差。如果结果不满意，可以继续调整，直到满足要求为止。

2.6 区间生成

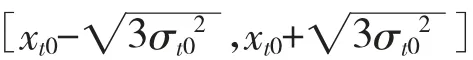
3 实例计算

下面将基于上述模型和方法，对某自行火炮节制杆进行在最大射程角下的稳健优化。优化后各设计变量的变化区间如表3 所示。为了满足稳定性和节制环限制要求，该节制杆的直径需大于39.2 mm，小于62.3 mm。由表3 可知：优化后的节制杆尺寸是满足稳定性和节制环限制要求的；节制杆各折点处的直径和轴向距离敏感程度是不一样的；节制杆前端折点处的直径和轴向距离更加敏感。

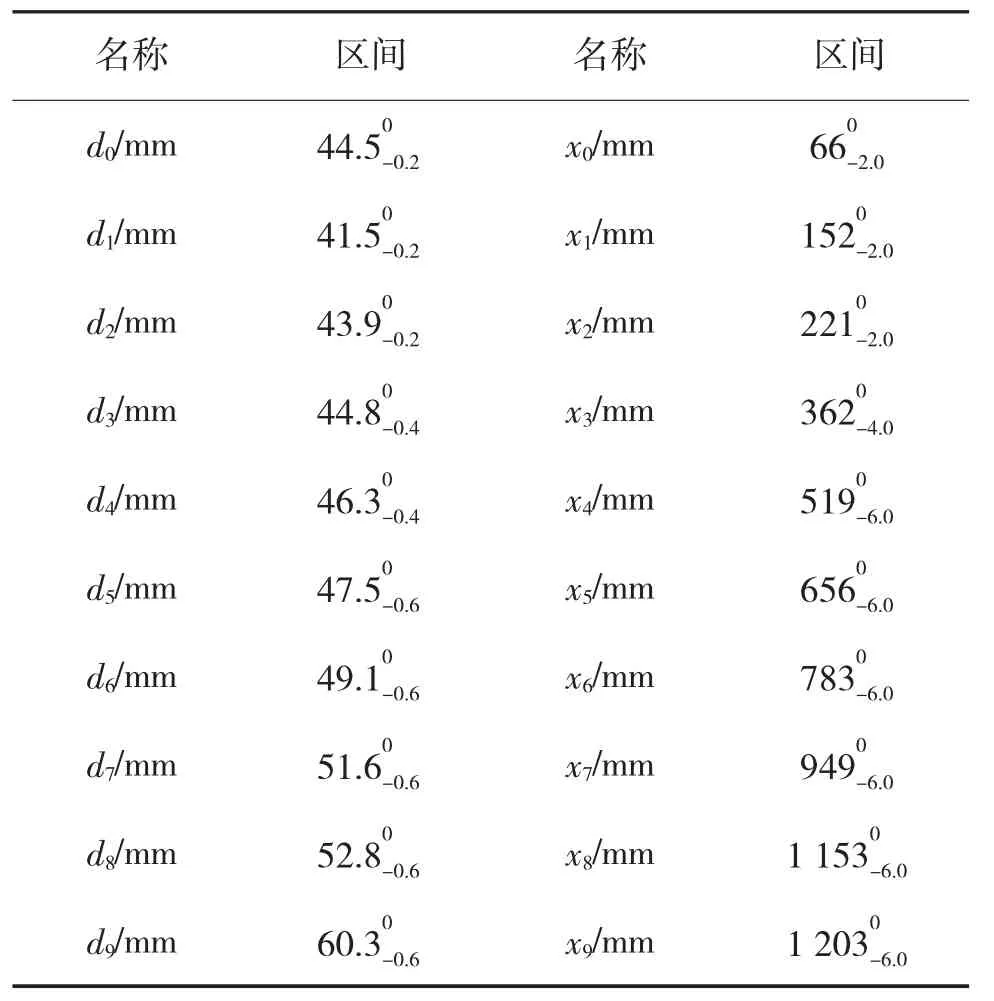
表3 设计变量变化范围

当所有设计变量都取均值时，后坐阻力随后坐位移的变化如图2 所示。由图2 可知：优化后的平均最大后坐阻力明显小于优化前的平均最大后坐阻力但是平均后坐长度变长了。

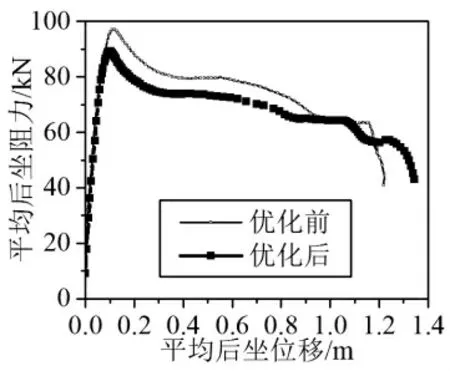
图2 平均后坐阻力对比图

优化前后最大后坐阻力和后坐长度的变化范围如表4 所示。由表4 可知：优化后，最大后坐阻力均值降低了12.2%，相应的波动范围降低了32.3%；后坐长度均值降低了12.9%，相应的波动范围降低了25.0%；最大后坐阻力和后坐长度都满足约束条件。综上所述，上述稳健优化是成功的，第2 节提供的方法是可行的。