基于球状模型的短波频率泛克里金重构算法*

徐 池，韩 东，田晓铭，李 梁

（海军大连舰艇学院 大连 116018）

0 引言

短波通信具有通信距离远、开通迅速、机动灵活、网络重构便捷等优点，是军事通信和应急通信的重要手段之一［1-4］。例如，美国罗克韦尔·柯林斯公司在近几年多次成功演示了新一代宽带高频通信系统，用以验证美军在无卫星通信保障条件下的远程通信能力。

随着通信技术的不断发展，短波通信在宽带高速数据传输、远距离通信链路自动建立、综合组网协议构建等方面都取得了一定的技术突破［5］。其中，短波通信频率的优选一直是短波通信中的关键问题之一，特别是在军事通信领域，短波通信频率的优选需要综合多种技术手段，进而满足军事训练、作战需求。按照技术原理划分，短波通信频率的优选可分为频率预测和频率探测两大类，频率预测又可以进一步划分为在时间维上的频率预测和空间维上的频率重构，时间维的预测和空间维的重构适用于不同的应用背景。当前，国内外学者研究出了很多时间维上的频率预测方法，例如神经网络、模糊小波、混沌算法等预测方法［6-7］。空间维上的频率重构技术也取得了一定的发展。经过研究验证和实际应用表明，空间局部估计（或称空间局部插值）法在短波频率重构中具有较好的使用效果，充分提高了已广泛采集的、大量的短波频率数据的使用效益［8-9］。本文利用短波通信实测频率数据，构建基于球状模型的泛克里金法，将方法应用于短波频率重构中，验证方法的可行性，并研究短波频率沿不同漂移方向的变化情况，给出具体应用流程及计算过程。

1 泛克里金法基础理论

克里金法能够基于采样数据反映的区域化变量的结构信息（由变异函数或协方差函数提供），根据待估点有限领域内的采样点数据，考虑样本点的空间相互位置关系、与待估点的空间位置关系，对待估点进行一种无偏最优估计，并且给出估计精度［10］。常用的克里金法有简单克里金法、普通克里金法、泛克里金法等，考虑到电离层变化的漂移特性、采样数据的稀疏程度等因素，可将泛克里金法引入短波频率重构中，在相关变程内构建符合频率数据变化规律的球状变异函数模型，沿不均匀体漂移方向建立频率数据的漂移方程，基于大量短波通信实测频率数据反映的空间结构信息［10-12］，对该区域内未知点处的区域化变量进行无偏最优估计。

1.1 泛克里金法基本原理

泛克里金法是一种基于空间分布的结构性和随机性对区域化变量进行无偏最优估计的方法［13］。该方法首先分析数据中存在的变化趋势，获得拟合模型；其次，对残差数据进行克里金法分析；最后，将趋势面分析和残差分析的克里金法结果加和，得到最终结果。

当一个变量呈现空间分布时，就称之为区域化变量Z（x）。这种变量反映了空间某种属性的分布特征。泛克里金法中非平稳区域化变量Z（x）可分解为漂移m（x）、涨落R（x）两部分，即Z（x）=m（x）+R（x）。漂移m（x）=E［Z（x）］定义为Z（x）的数学期望，也具有非平稳性，通常采用多项式的表达形式：

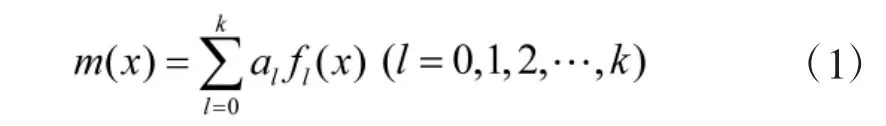
可依据变量具体的漂移特性写成与坐标有关的函数。已知某区域内n 个样本邻域点xi（i=1，2，…，n）处的区域化变量为Z（xi）（i=1，2，…，n），则待估域内未知点x0处Z（x0）的估计量为：

其矩阵形式可写为：

其中，γij为变异函数值。

1.2 基于球状模型的变异函数

变异函数是以区域化变量理论为基础建立的基本函数，能够描述区域化变量的结构性、随机性变化。变异函数理论模型主要包括球状模型、高斯模型、指数模型等［5］。其中，球状模型又称Matheron（马特隆）模型，在实际应用中发现95%以上的实验变异函数（h，γ*（h））离散数据均可采用该模型进行拟合，适用范围广泛。球状模型的表达式可具体参考文献［10］。

需要强调的是，为了定量地描述整个区域的变量特征，必须给出实验变异函数曲线配以相应的理论模型，而要使该理论模型精确、真实地反映变量的变化规律，就需要在建立理论模型过程中对模型进行最优拟合，即根据实验变异函数值，选择合适的理论模型来拟合一条最优的理论变异函数曲线，最优拟合的过程实质是拟合最优模型的过程。变异函数理论模型的最优拟合主要包括3 个步骤：确定变异函数模型形态；模型参数的最优估计；模型拟合评价。变异函数最优拟合主要是曲线拟合，因此，可将曲线模型先进行适当变换，变换为线性模型，然后可用最小二乘法原理估计模型参数，最小二乘法拟合的优点是简单方便。

2 基于泛克里金法的短波频率重构算法验证

基于某型短波频率管理系统中大量的通信实测数据，选取2015 年某日上午某区域内移动通信台站与同一固定台站通信的可用频率作为验证的样本数据，利用其中的部分数据对基于球状模型的变异函数进行构建，其余数据用于验证泛克里金法应用于短波频率重构算法的可行性及有效性。

2.1 基于球状模型的变异函数构建

在短波频率重构中，建立基于球状模型的变异函数的具体步骤为：

1）求解任意通信两点之间的滞后距h：

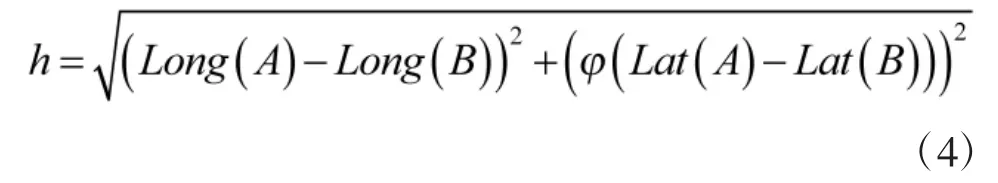
其中，Long（A）表示通信A 处的地理经度，Lat（A）表示通信A 处的地理纬度，φ 是电离层距离转化比例系数。

2）依据实际情况设置一定的距离间隔并将样本数据的滞后距h 按照距离间隔进行划分，依次取各区间内h 的平均值［9］。基于式（5）计算出各区间平均滞后距所对应的实验变异函数γ*（h）：

3）基于球状模型的一般表达式，通过最小二乘法对样本频率数据下的实验变异函数进行球状模型拟合，获得研究区域内变异函数γ（h）与滞后距h的关系曲线。变异函数最优拟合主要是曲线拟合，因此，可将曲线模型先进行适当变换，变换为线性模型。这里选用最小二乘法原理估计模型参数，最小二乘法拟合的优点是简单方便。

此例中依据实际情况设置距离间隔为2 km，各间隔区间内的平均滞后距h 及其相应的实验变异函数γ*（h）的计算结果如表1 所示。

表1 实验变异（h，γ*（h））函数数据

基于最小二乘法的线性表达式对离散数据（h，γ*（h））进行曲线拟合，构建出相应的理论变异函数（h，γ（h）），球状模型的最小二乘表达如表2 所示，模型构建曲线如图1 所示。其中，a≈35.666 6，c≈135.356 2，c0≈8.349 2。

表2 基于最小二乘法的球状模型表达及参数求解

图1 球状模型拟合曲线

将各参数值代入球状模型的一般表达式中，可得研究区域内的变异函数为：

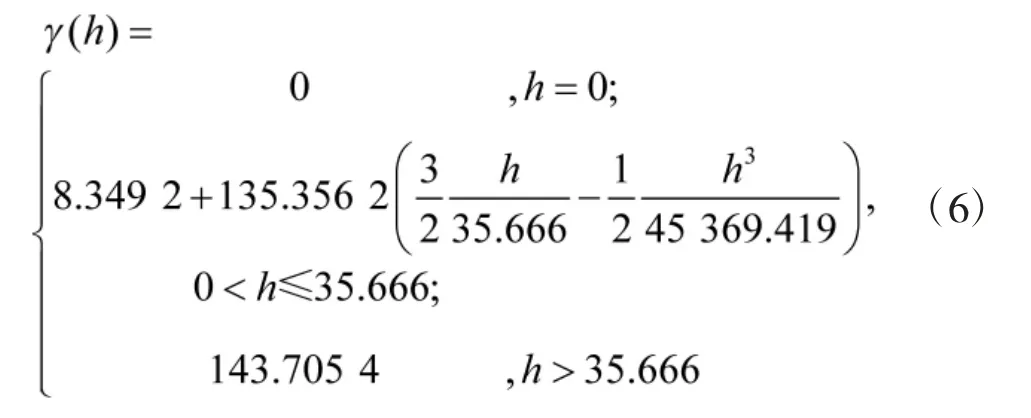
2.2 基于泛克里金法的短波频率重构

随机选取5 个未参与变异函数模型构建的频率样本数据，其通信地理位置分别记作A 点～E点，地理位置及短波通信可用频率实测值如表3所示。

表3 A 点～E 点地理位置及实测短波可用频率

假设某点为待重构的未知通信点，简称频率未知点，其余各点为已知通信频率数据的邻域点，通过交叉验证的方式，仿真验证基于球状模型的泛克里金法的可行性。这里以重构A 点频率为例，给出具体的计算过程。

第1 步：计算理论变异函数值。

由式（4）计算各邻域点与未知点及任意邻域点之间的滞后距，并通过球状模型表达式（6）获得相应的理论变异函数值，其中电离层距离转化比例系数取平均值φ=2。表4 记录了A 点为未知点时球状模型下（h，γ（h））的值。

表4 上三角是滞后距下三角是理论变异函数值

第2 步：建立泛克里金法漂移方程。

由于电离层等离子体在水平方向上存在漂移，且不均匀体的漂移速度沿传播方向线性增加，因此，需要分析研究短波频率数据沿经（纬）度方向、水平方向存在线性漂移时的重构效果。以分析频率数据沿经度方向上的漂移特性为例，其漂移表达式可设为：

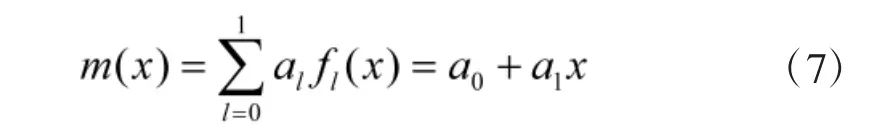
其中，x 表示经度；如仅分析频率数据沿纬度方向上的漂移特性时，其表达式不变，此时x 表示纬度；若需分析频率数据沿经、纬度两个方向（即水平方向）上的漂移特性时，其漂移表达式可设为：

其中，x 表示经度，y 表示纬度。

结合频率数据的漂移特性，在描述研究区域内短波频率沿经（纬）度方向变化时，将漂移式（7）代入泛克里金方程组（3），利用邻域点（B 点～E 点）的地理位置信息及通信频率数据对未知点A 处的短波频率进行重构，可获得泛克里金方程组矩阵形式表达式：

第3 步：求解泛克里金法漂移方程重构值。

将基于球状函数模型计算的理论变异函数值A点～E 点的纬度及B 点～E 点的频率数据代入矩阵式（9）中，经运算可得频率数据沿纬度方向漂移时A点处的短波频率重构值Z*（xa）为：

根据上述步骤，同理可知频率数据沿经度方向漂移时A 点处的短波频率重构值Z*（xa）为：

在研究某区域内短波频率沿水平方向变化时，将漂移式（8）代入泛克里金方程组，利用已知邻域点（B 点～E 点）的地理位置信息及通信频率数据对未知点A 处的频率进行重构，可获得泛克里金方程组矩阵形式表达式：

将基于球状函数模型计算的理论变异函数值A点～E 点的经度及B 点～E 点的频率数据代入矩阵式（10）中，经运算可得频率数据沿水平方向漂移时A点处的短波频率重构值Z*（xa）为：

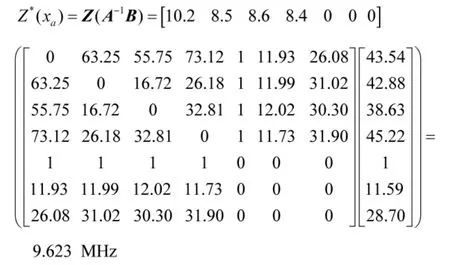
依据上述方法对其余各点的通信频率进行重构，基于变异函数球状模型研究经（纬）度、及水平方向的漂移变化对频率重构的影响，其重构结果如表5 所示。

表5 频率数据沿不同方向存在漂移时球状模型下的泛克里金重构值（MHz）

2.3 重构结果的验证与分析

为了进一步研究基于球状模型的泛克里金法在短波频率重构中应用的有效性，分析研究区域内短波频率数据的变化特征，将重构获得的频率值和基于“亚大模型”的频率预测值与实际频率值相比较，计算相对误差。依次计算球状模型下频率沿不同漂移方向变化时其余各点的相对误差，记录于表6 中。

表6 频率数据沿不同方向漂移时球状模型下的相对误差及相对误差均值（%）

“亚大模型”由中国电波传播研究所于1987 年提出，在北纬65°至南纬40°、东经60°至东经150°范围内具有良好的应用效果。为避免参数换算误差，2007 年又对“亚大模型”进行了修正，提出了新版“亚大模型”，新版模型重点提高了低纬度地区的预测精度［14-15］。根据通信双方地理位置信息、通信时间、太阳黑子数等输入参数，基于“亚大模型”的频率预测结果及与实测值的相对误差如表7 所示。A 点～E 点频率实测值、预测值和重构值的比较曲线如下页图2 所示。

表7 “亚大模型”预测结果

图2 各点频率实测值、预测值、重构值比较曲线

泛克里金重构算法考虑了电离层的变化，引入了随经度、纬度、水平方向的漂移方程，利用相同样本数据，比较泛克里金重构算法与文献［8］中普通Kriging 法的重构精度。基于“亚大模型”的频率预测结果及与实测值的相对误差如表8 所示。A 点～E 点频率实测值、预测值和重构值的比较曲线如图3 所示。

表8 普通Kriging 法频率重构结果

图3 各点频率实测值、普通克里金法重构值、泛克里金法重构值比较曲线

通过基于上述方法的大量数据分析，结合该样本区域短波通信实际应用情况［16-22］，可得出如下结论：

1）基于球状模型的泛克里金法适用于短波频率的重构。基于某海域已采集的大量短波通信实际数据，随机选取样本点条件下的验证结果表明：在频率数据球状模型拟合条件下，各漂移方向上重构结果的相对误差均值均低于4.5%；在沿纬度方向构建漂移方程时，单点的重构相对误差值低至0.188 2%，具有较好的重构精度。可见，采用泛克里金法在空间相关变程内进行频率重构，能够预测未知区域的短波通信用频。

2）基于泛克里金法的短波频率重构效果优于中长期的频率预测。基于本次选择的样本区域数据，相比较基于“亚大模型”的频率中长期预测，基于泛克里金法的短波频率重构结果更接近实测值，重构精度能够满足实际使用需求。基于亚大模型的预测软件是当前比较常用的中、长期频率预报软件，分别具有点对点、点对面、面对面通信频率预测功能。然而，软件在进行电离层传播模型构建时，有关中国区域电离层结构信息仍然较少，这也导致该软件的适用范围受限，在该样本数据中，预测值的相对误差均值达到了9.811 4%，预测精度有限。

3）泛克里金重构方法的短波频率重构精度高于普通克里金方法。建立在区域化变量结构信息基础上的泛克里金重构方法满足变量非平稳性的需求，考虑了变量局部漂移的影响，能够在空间相关变程内对区域化变量进行无偏最优估计。基于短波频率管理系统中大量的通信实测数据，通过样本数据重构精度比较发现，普通克里金方法重构的相对误差均值为6.427 8%，误差大于泛克里金重构，但部分样本点的精度较高。例如样本中的B 点，相对误差仅为1.811 9%，主要原因可能是该收发两点的电离层反射点受电离层漂移影响较小。

4）根据具体的重构区域电离层特点构建漂移方程。基于研究区域内电离层不均匀体、等离子体的线性漂移特性，分别沿经度方向、纬度方向及水平方向构建漂移方程。通过表6 可以观察到，在符合短波频率数据空间特征的球状模型的交叉验证中，漂移方程的构建方向为纬度方向时，重构效果最佳为2.125 7 %，且各点的重构相对误差均低于4.5%，重构效果较好。而当沿经度方向或水平方向建立漂移方程时，其重构效果稍逊于纬度方向，特别是在沿经度方向构建方程的情况下，C 点处重构值与实测值的相对误差高达13.205 7%。表明本次样本区域内短波频率数据具有沿纬度方向漂移的变化特点，在泛克里金法应用于该区域的短波通信频率重构时，可直接采用沿纬度方向构建的漂移方程。值得说明的是，不同区域对应的电离层不均匀体、等离子体的漂移方向可能不同，在实际应用中，可先对重构区域的电离层特点进行分析研究，以确定适合电离层变化方向及变化特征的漂移方程，进而实现基于泛克里金法的短波频率重构。

3 结论

针对短波通信频率优选技术的不同应用需求，基于短波频率在空间维上的重构原理，利用前期采集的某海域短波通信实际频率数据，选取在空间局部估计中广泛应用的球状模型，构建了符合频率数据变化特征的基于球状模型的变异函数，并建立了沿经度、纬度、水平方向的漂移方程。利用样本数据验证了泛克里金法在短波频率优选中的适用性及可靠性，验证结果表明，频率重构算法能够为短波中远程通信的频率优选提供技术支撑和手段。重构算法有效利用了历史数据信息，依据通信频率的空间相关性进行估计，弥补了以电离层模型、传输模型为基础的频率预测方法手段的单一性和预测精度存在局限性的不足，同时可以有效避免探测方法中通信双方进行探测选频所带来的耗时长、占用信道、目标易暴露等问题。

样本数据的漂移特性影响着频率重构精度，因此，可进一步研究各区域内电离层的变化特征，构建适用于不同样本数据的沿经度、纬度方向及水平方向变化的漂移方程，完善基于球状模型的泛克里金法。同时，考虑重构算法的工程软件化，研究中变异函数理论模型的最优拟合选用了简单方便的最小二乘法，该方法由于对实验变异函数曲线中开端几个点的重要性认识不足，导致曲线有时不太理想，下一步可考虑选用加权回归方法予以克服。