一种丝驱连续体手术机械臂的设计及其运动学分析*

卢佳佳，冯显英*，杜付鑫，岳明君，屈梁成

(1.山东大学 机械工程学院，山东 济南 250061；2.山东大学 高效洁净机械制造教育部重点试验室，山东 济南 250061)

0 引 言

因具有减少患者创伤和出血量、缩短住院时间、术后恢复快等优点，微创手术、单孔手术和自然孔口手术受到广泛应用[1]，这类手术通常是在体内相对密闭的空间中来完成夹持、剪切、消融等任务。

由于缺乏足够数量的自由度，传统离散机械臂无法适用于狭窄拥挤的体内环境[2]，由此推动部分学者们开始研究多冗余自由度、高灵活性和安全性的柔性机械臂。

柔性机械臂一般可分为两种：软体与连续体。(1)软体机械臂大多是利用仿生技术，从行为或功能上模仿自然界中的生物，如章鱼触手、大象鼻子等，一般多由硅胶、橡胶等弹性材料制成[3-5]，其理论上具有无限自由度。(2)连续体机械臂通常是将若干个相同或相似单元两两串联[6]，或者是在管状材质侧壁切割出切槽[7]，与软体机械臂相比，其具有有限个自由度，但承受负载能力、可操纵性优于软体机械臂。

连续体机械臂的多冗余度特征使其较传统离散机械臂获得了优良灵活性，但同时也导致其正逆运动学求解变得困难。因此，许多学者采用不同方法对连续体机械臂的运动学问题进行了深入研究。HANNAN和WALKER[8]提出了分段常曲率假设，并基于这个假设建立了驱动丝长度到机械臂末端位姿的正运动学映射；TANG等[9]同样基于分段常曲率假设建立了驱动空间到工作空间的正运动学模型；文献[10-11]针对所设计的切口式连续体机械臂基于悬臂梁理论建立了驱动力与机械臂末端位置之间的正逆运动学模型；GREIGARN等[12]使用了基于雅可比矩阵求解连续体机械臂逆运动学的方法；XU等[13]利用椭圆积分给出了多骨干连续体机械臂瞬时正运动学解析公式，建立了配置空间到工作空间的映射关系；文献[14]提出了一种准静态条件下基于有限元方法的变曲率连续体机械臂正逆运动学求解方法，建立了驱动丝张力与末端位置的相互映射；文献[15]利用Pythagorean Hodograph曲线建立了连续体机械臂末端位置到连续体机械臂长度的逆映射模型。

上述方法虽然在连续体运动学方面解决了部分问题，但均没有推导出连续体机械臂末端位置到驱动丝长度的逆运动学解析解，使得运动学求解效率较低，不能满足丝驱连续体机械臂实时控制的要求。

针对上述问题，笔者设计一种新型连续体机械臂。

1 连续体机械臂结构设计

连续体机械臂设计如图1所示。

图1 连续体机械臂设计

图1中，机械臂主体是由若干个中间单元、基座、末端单元和橡胶软管组成，橡胶软管作为骨架将所有单元依次串联起来，每两个单元之间通过球面接触形成一个关节，关节的偏转由驱动丝收放变化来控制。机械臂由两组驱动丝控制其运动，驱动丝均匀分布在同一圆周上，一组驱动丝收放可控制机械臂在平面内的正向和反向弯曲，两组驱动丝同时收放可实现机械臂在XY平面内任意一个方向的弯曲运动。

机械臂最大直径为20 mm，末端可固定小型手术器械，通过控制机械臂运动能够实现手术器械在拥挤复杂人体环境下的安全定位。

2 运动学模型

运动学模型旨在建立起驱动丝长度与连续体机械臂末端位置之间的相互映射关系。首先，笔者建立了驱动空间、形态空间和工作空间，驱动空间包含驱动丝长度，形态空间包含机械臂弯曲角度和弯曲方向，工作空间包含机械臂末端位置。

正逆运动学映射建立过程均分两步进行，正运动学映射建立顺序为“驱动空间—形态空间—工作空间”，逆运动学映射建立顺序则与此相反。

2.1 正运动学模型

连续体机械臂关节是由两个相邻单元通过球面接触构成，连续体机械臂关节参数如图2所示。

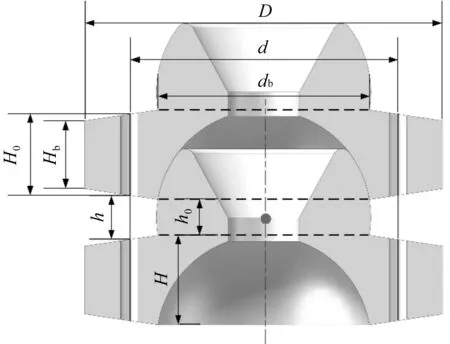
图2 连续体机械臂关节参数

由相似原理可知：

(1)

(2)

式中：D—单元的最大直径；d—驱动丝均匀分布的圆周直径；H，H0—单元内驱动丝长度和单元高度；Hb，db—单元的倒角尺寸；h，h0—关节无偏转时两个单元之间的驱动丝长度和间距。

当关节在驱动丝平面内偏转θ角度时，根据几何关系可推出：

(3)

式中：hl，hr—两个单元间成中心对称的两根驱动丝长度。

假设连续体机械臂具有N个关节的，根据分段常曲率假设，每个关节偏转角度相等，均为θ，则可得到：

(4)

式中：Ll，Lr—机械臂内一组驱动丝长度；HB，HE—机械臂基座和末端单元高度；C—简化变量，C=NH0+HB+HE。

由式(3，4)可推出：

(5)

关节的偏转导致机械臂的弯曲运动，机械臂弯曲角度Θ可由下式得到：

Θ=Nθ

(6)

关节弯曲角度存在最大值，该值由关节的单元自身参数决定，可通过下式进行计算：

(7)

连续体机械臂通过两组驱动丝控制其弯曲运动，其截面如图3所示。

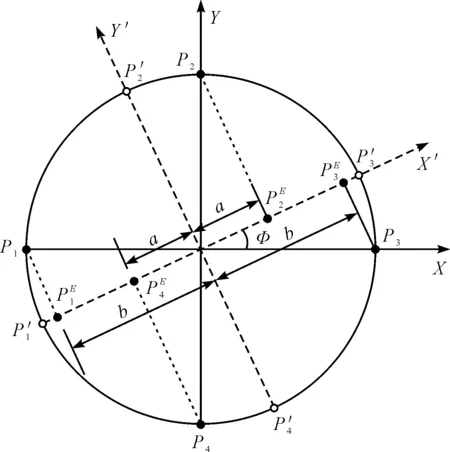
图3 连续体机械臂截面P1，P2，P3，P4—两组驱动丝位置；在虚轴X′上的等效点

假设机械臂沿与X轴夹角为Φ的方向弯曲，则机械臂内两组驱动丝的长度可由下式计算得到：

(8)

由公式(8)可推出Φ和Θ的计算公式：

(9)

(10)

至此，驱动空间到形态空间映射关系求解完毕。形态空间到工作空间的映射可通过D-H法建立。

连续体机械臂D-H坐标系如图4所示。

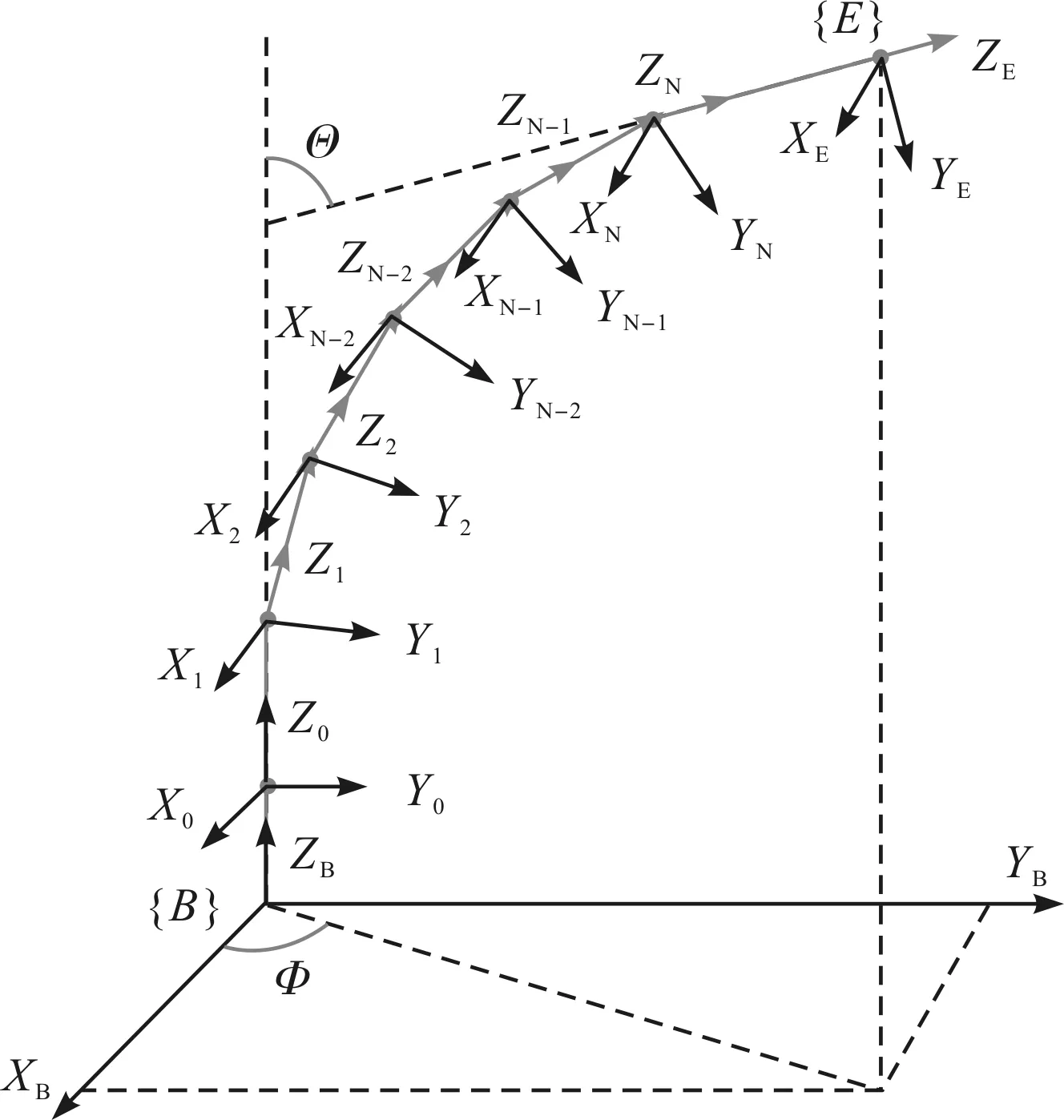
图4 连续体机械臂D-H坐标系

D-H坐标系包含基座坐标系{B}、末端坐标系{E}和0～N号关节坐标系。

假设每个关节的偏转角度为θ，弯曲方向为Φ，第i个关节的D-H参数如表1所示。

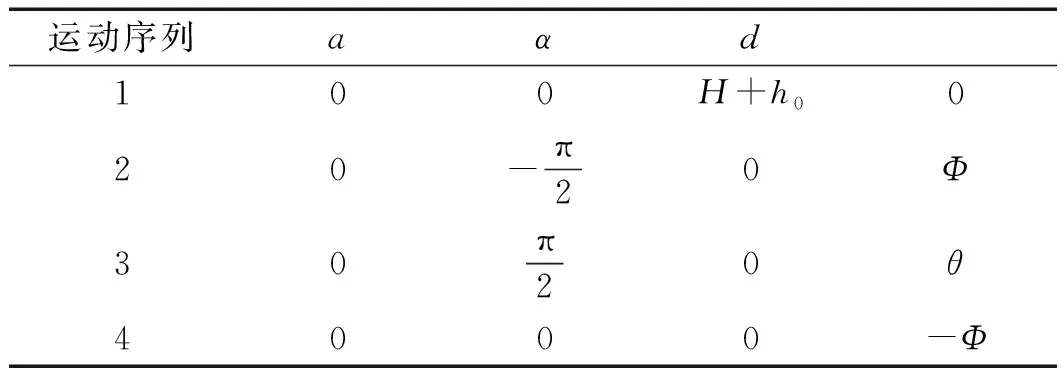
表1 第i个关节的D-H参数

根据所建立的D-H坐标系，可列出第i-1号关节坐标系变换到第i号关节坐标系的D-H参数。将以上运动序列的齐次变换矩阵依次相乘，可得到两个相邻关节坐标系的齐次变换矩阵：

i-1Ti=

(11)

式中：Sθ，Cθ，SΦ，CΦ—简化变量，Sθ=sinθ，Cθ=cosθ，SΦ=sinΦ，CΦ=cosΦ。

对连续体机械臂N+3个坐标系变换运用链式法则，即可得到{B}与{E}之间的齐次变换矩阵：

(12)

(13)

机械臂末端位置可用P=(x,y,z)T表示，其中：x,y,z—表征末端位置的笛卡尔坐标系三维坐标，并且有：

(14)

至此，形态空间到工作空间的映射关系求解完毕，连续体机械臂正运动学模型建立完成，得到了机械臂末端位置的解析解；给定驱动丝长度，即可求解出连续体机械臂末端位置。

2.2 逆运动学模型

逆运动学映射旨在求解机械臂末端位置到驱动丝长度的映射关系，逆运动学映射建立过程与正运动学映射相反，因此，首先要求解工作空间到形态空间逆运动学映射关系。

工作空间到形态空间映射如图5所示。

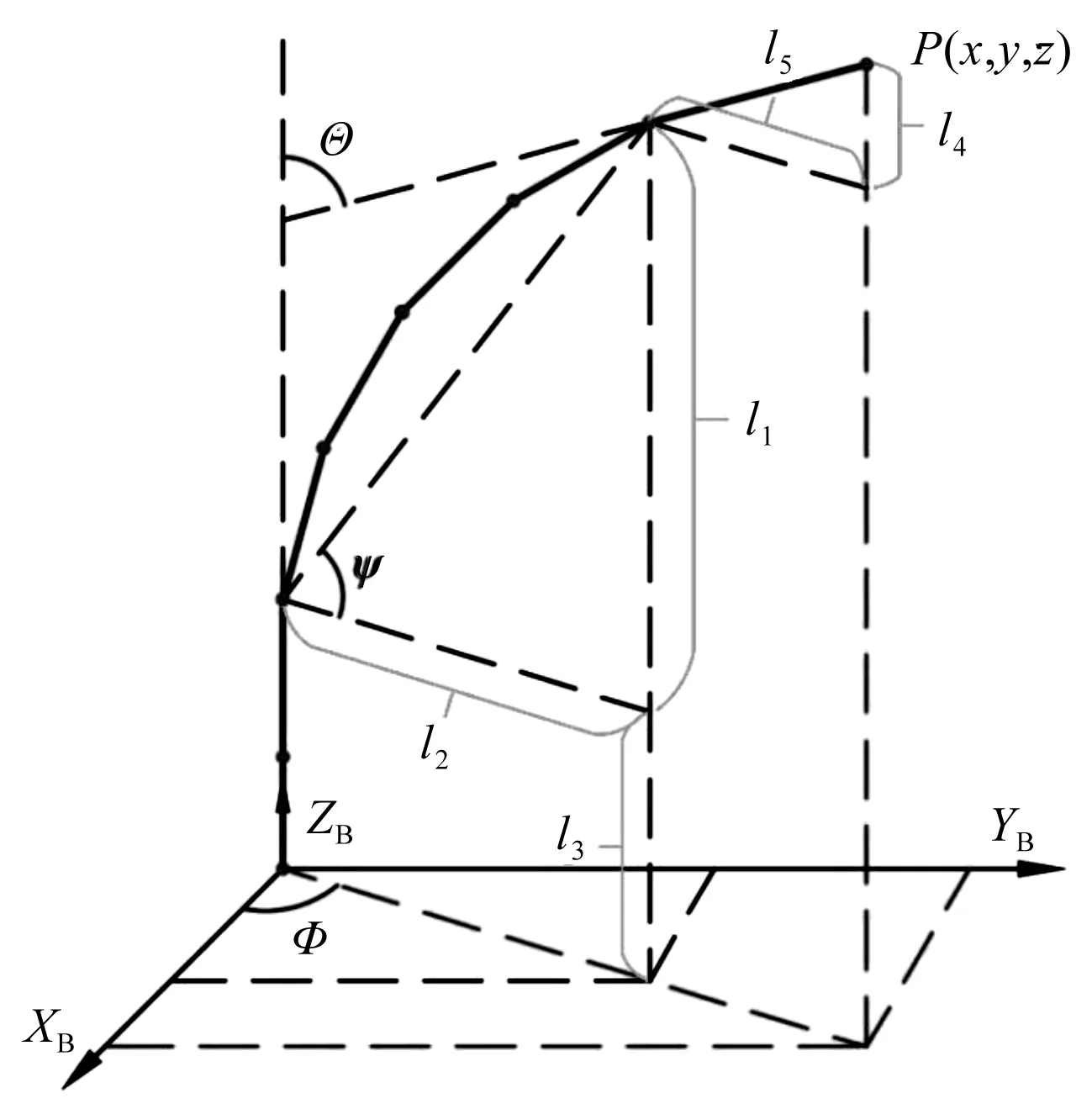
图5 工作空间到形态空间映射

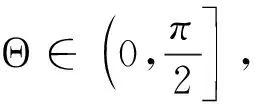
(15)

(16)

(17)

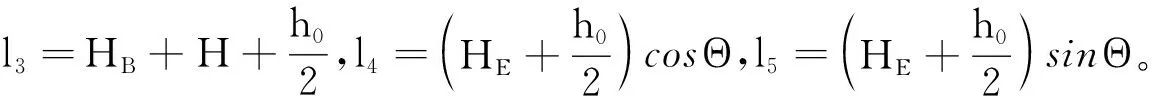
把式(16)代入式(17)，经化简可得到：

(18)

式中：C0—简化变量,C0=HE-HB-H。

式(18)共有一个实数解和两个非实数解，舍去其非实数解，即可得到连续体机械臂弯曲角度Θ的逆运动学计算公式：

(19)

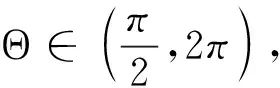
至此，工作空间到形态空间的映射关系求解完毕，形态空间到驱动空间的映射关系已由式(8)建立。连续体机械臂逆运动学模型建立完成，得到了如式(8，15，19)的逆运动学解析解；给定末端位置，即可求解所需驱动丝长度。

3 实验及结果分析

实验系统组成如图6所示。

图6 实验系统组成

该实验系统主要由连续体机械臂、舵机、控制器、上位机和Hikvision相机组成。

图6中，右下角为实验所采用的连续体机械臂；材料为DSM树脂，主体长度为85 mm。

连续体机械臂设计参数如表2所示。

表2 连续体机械臂设计参数

为方便测量机械臂末端位置坐标，机械臂末端固定了一个直径10 mm的白色透光小球。驱动丝采用超软钢丝，直径为0.5 mm，一端固定在机械臂末端，另一端固定在绕线盘上，每个绕线盘上固定一根驱动丝，实验中由舵机带动绕线盘转动定量改变驱动丝长度。利用Hikvision相机测量机械臂末端位置坐标，实验前已对相机进行标定，精度为±0.1 mm。

为使连续体机械臂运动更符合分段常曲率假设，实验中使用润滑脂对机械臂关节进行了润滑。实验过程中，依次改变驱动丝长度，使末端小球球心到达理论点附近，然后利用相机测量末端位置坐标。

实验误差绝对值如图7所示。

图7 实验误差绝对值

图7中，方形标记、星形标记、圆形标记和菱形标记分别表示距离误差、X轴方向误差、Y轴方向误差、Z轴方向误差。实验结果表明，位置平均误差小于2.56 mm，并且均方根误差最大不超过1.18 mm，分别占机械臂总长度2.57%和1.18%。

实验误差主要来自于以下原因：(1)由于机械臂的制造误差使得机械臂的实际运动不满足分段常曲率假设；(2)实验装置刚度不足导致驱动丝实际变化长度与理论计算值不符；(3)相机测量误差。

4 结束语

笔者提出了一种丝驱动连续体机械臂，该连续体机械臂具有两个弯曲自由度，能实现较大的弯曲变形；基于分段常曲率假设，通过将正逆运动学映射过程分别分成两步进行，建立了驱动丝长度、机械臂弯曲方向和弯曲角度与机械臂末端位置三者之间的相互映射关系；并结合D-H法和几何分析法，建立了连续体机械臂正逆运动学模型，推导出了正逆运动学解析公式。

实验结果表明，平均实验误差不超过2.56 mm，约为机械臂总长度的2.57%。实验结果表明，所提出运动学模型具有有效性，并可应用于类似的连续体机械臂运动学求解。但由于树脂材料加工的局限性，导致机械臂结构尺寸和关节间摩擦力较大，降低了机械臂运动精度。

下一步笔者将通过更换金属材料以减小机械臂尺寸和关节间摩擦力，并寻求建立更加精确的运动估计模型，以提高机械臂的运动控制精度。