基于流固耦合的多级压气机叶片振动瞬态动力学分析
2020-09-22高通
高通
(惠阳航空螺旋桨有限责任公司,河北 保定 072100)
基于MFX-ANSYS/CFX 为数据耦合平台,研究多级压气机额定工况下叶片在流场中瞬态动力学响应,得到叶片位移响应及监测点压力变化规律,并研究判定叶片是否发生颤振的方法,以期进一步了解多级气机叶片的颤振特点。
1 流固耦合计算方法
流固耦合力学是用来研究可变形固体在流场作用下的瞬态响应,以及固体变形后对流场的反作用关系,它涉及计算流体力学与结构动力学等交叉学科的内容,其重要特征是两相介质之间的相互作用。
流体流动要遵循三大定律,质量守恒、动量守恒和能量守恒定律:

动力学的通用运动方程为:
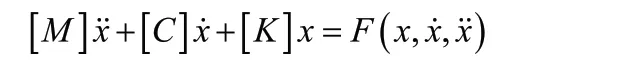
此方程描述的是典型的非线性自激振动系统。对有限元模型进行结构动力学分析时,需要考虑结构模型的惯性、刚度和阻尼特性。结构动力学分析包含众多研究内容,不同的分析类型对应求解不同形式的方程。在流固耦合问题中,需要将流体域中的基本方程以及结构域的动力学方程进行联立求解。交界面处应满足流体与固体的位移、热流量、温度、应力等相等。

将耦合交界面上的流体压力施加到结构动力学方程,结构动力学方程变形为:
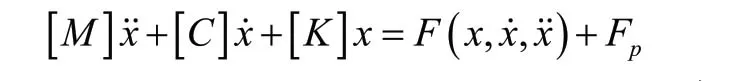
式中:pF为耦合交界面上的流体压力矢量。
2 压气机分析模型
本研究以公司生产的某型号压气机为例,压气机为二级结构,包括两级动叶和两级静叶。对压气机进行流固耦合分析,需要对固体域及流体域分别建模。
固体域两级动叶主要分为叶片、套筒及金属接头三个部分,为了模拟压气机叶片的运动状态,均对各部位进行实体建模。为了更好地反映叶尖及靠近叶身表面的流体流动特性,对叶顶间隙及叶身前后缘分布的网格进行加密处理,套筒及金属件处变形较小,网格较稀疏。仿真模拟叶片的额定工况点,转速为411r/min。金属接头部位采用固定约束,套筒部位边界条件为限制径向的自由度。流体域计算的气动力以压力的形式施加在叶片表面。
流体有限元网格由计算流体力学软件NUMECA进行划分,求解整级叶片叶栅通道的流场计算量非常大、比较耗时。同时,由于压气机转子在结构上有很好的循环对称性,因此,本研究选取压缩机叶片单通道模型进行数值计算。流体域网格采用六面体单元,如表1 所示。通过对网格进行无关性验证,最终选取网格数量为313 万。叶片采用随区域运动壁面边界,前后壁面设置为旋转周期性边界,机匣应用无滑移壁面条件,转静子交界面采用混合平面,利用隐式算法和二阶迎风格式进行求解。

表1 流场边界条件
3 叶片瞬态动力学分析
双向流固耦合分析以流场稳态计算结果作为初场,时间步的选取依赖叶片固有频率,综合考虑固体域和流体域对时间步长的特殊需求,这里选取时间步长为5e-4s。为了解气动载荷作用下压缩机叶片的瞬态动力学特性,需要在压缩机叶片表面设置监测点。如图1 所示,图中黄色标记点即为监测点位置。P1、P2为压力监测点,分别位于第一级动叶和第二级动叶尾缘,动静叶片所在流域交界面处。M1、M2为位移监测点,分别设置在位移变化最大的动叶叶顶处。

图1 监测点位置示意图
图2 表示各级动叶监测点物理参数变化时域图。由压力检测点数据可知,波动明显呈现周期变化,数值平均值与稳态计算解果相吻合。随着数值模拟的进行,监测点在每个旋转周期内的压力波动逐渐减小,达到稳定,表明叶轮流道内的非定常流场流动逐步达到“稳态”。两处监测点变化频率也基本相同,作用在压缩机叶片上的气动力为明显的强迫振动。

图2 监测点数值变化时域图
对各级动叶位移监视点时域图进行频谱分析,结果如图3 所示。
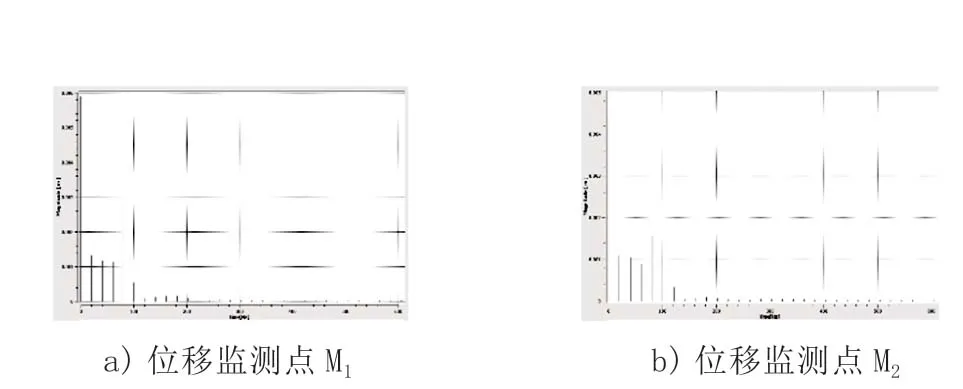
图3 位移监测点信号频域分析图
压气机叶片振动频率主要集中在低频域,两级叶片在额定工况下的振动频率小于各叶片的一阶动频,表明叶片在此工况下不会发生共振。选取M1、M2网格位移的响应敛散性来判断叶片是否发生颤振。由各级动叶位移监测点时域图可知,M1、M2处位移响应是逐渐收敛的,故可以以此来判定压气机叶片在这种工况下不会发生颤振。
4 结语
本研究以多级压气机为研究对象,基于ANSYS/CFX 为数据耦合平台对多级压气机单通道模型进行流固耦合数值计算,分析了额定工况下流场的压力分布及叶片的瞬态动力学响应特性,主要研究总结如下:叶片瞬态动力学分析表明,流场内存在周期性变化的压力。对叶片顶点的振动进行频谱分析,结果表明,叶片的振动主要在低频域内。叶片在额定工况下的振动频率小于叶片的一阶动频,表明叶片在此工况下不会发生共振。分析各叶片在额定工况下顶点位移的敛散性表明,叶片在瞬态气动力的作用下振动幅值逐渐减小并且趋于稳定,表明叶片的位移响应是收敛的,在额定工况下,叶片不会发生颤振。基于这种方法,可对多级压气机叶片的颤振特性进行预测分析。
