广义回归神经网络在冗余捷联惯导故障诊断中的应用研究

2020-09-22乔鹏超孙湘钰罗广地

导航定位与授时 2020年5期

乔鹏超，孙湘钰，罗广地

(哈尔滨工程大学自动化学院，哈尔滨 150001)

0 引言

冗余捷联惯导故障诊断技术是提高冗余系统可靠性[1]的有效途径，故障诊断技术要求算法具有反应速度快、故障诊断准确、能实时诊断和算法易实现的特点，是冗余配置捷联惯导算法研究的一个难点。Kevin C Daly等[2]基于统计方法提出了广义似然比法；金宏等[3]以对某个轴故障最敏感为评价指标，提出了最优奇偶向量法；Duk Sun Shim等[4]基于矩阵向量的奇异值分解，提出了奇异值分解法。这些方法在实际使用时，由于捷联惯导输出存在安装误差、刻度系数误差、常值偏差等测量误差[5]，导致必须使用更大的门限检测值[6]，使得虚警率增大，系统的可靠性降低。针对测量误差影响故障诊断效果的问题，文献[7-9]提出了利用Kalman滤波方法估计误差，然后采用补偿后的等价向量[10]进行故障诊断。上述方法在实际使用中都收到了比较良好的效果，但都要求动态误差模型和较准确的噪声统计特征。

本文提出了基于广义回归神经网络(Generali-zed Regression Neural Network，GRNN)的故障诊断方法，在传感器故障诊断数学模型未知的情况下，对传感器单故障和多故障的故障诊断问题进行了研究。

1 GRNN网络模型

神经网络在故障诊断方面具有以下优越性[11-12]：1)可避免数据分析和建模工作，通过观测样本神经网络就可以找到隐藏的信息；2)处理数据速度快，不需要进行大量数学运算，信息存储和处理合二为一；3) 具有实时性。由于神经网络之间的并行计算结构，神经网络具有很强的集体计算能力，完全可以实时估计出所求的值。

GRNN结构[13]是一种基于记忆模式的具有单隐层的三层前馈网络,其结构如图1所示。

图1 GRNN网络结构图Fig.1 GRNN block diagram

GRNN理论基础是非线性回归分析[14]。非独立变量Y相对于对立变量x的回归分析，实际上是计算具有最大概率的y。设随机变量x和y的联合概率密度为f(x,y)，已知x的观测值为X，则y相对于X的回归，即条件均值为

(1)

(2)

式中，Xi和Yi为随机变量x和y的样本观测值；n为样本容量；p为随机变量x的维数；σ为带宽系数，也称作平滑因子。

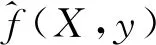
(3)

(4)

GRNN的输入神经元数和输出神经元数分别取决于系统输入和输出变量数，隐含层神经元数会自动调整，直到满足均方误差。GRNN平滑参数σ对其性能有很大影响。理论上，σ越小，对函数逼近越精确，但逼近过程越不平滑；σ越大，逼近越平滑，但逼近误差越大。所以在网络训练过程中，要选择合适的σ值[15]。

2 故障诊断算法

2.1 GRNN网络训练

根据冗余捷联惯导传感器故障诊断模型，作出如下假设。假定该冗余配置方案的n传感器，满足以下条件：

1)任意k个传感器Xk都能以精度ε计算出其余n-k个传感器Yk的输出(k≥3)。

(5)

2)Xk中的任意一个或一个以上传感器发生故障，均会导致Yk输出值发生改变。

3)系统中同时出现故障的传感器不超过n-(k+1)个。

本文以6传感器(陀螺或加速度计)正12面体冗余配置的捷联惯导系统为例(见图2)，验证了所提算法的有效性。在满足上述条件的情况下，每一对Xk和Yk组合训练一个多输入多输出(Multi-Input Multi-Output, MIMO)的GRNN，共可以训练K个。

(6)

在GRNN训练中发现，如果用同一个平滑参数训练MIMO网络，会导致输出估计误差较大。为了减小该误差，将上述MIMO网络分为3个多输入单输出(Multi-Input Single-Output, MISO)网络进行训练。又由于每个传感器均存在测量噪声，所以训练时应避免使参数误差估计过小而出现过拟合现象。

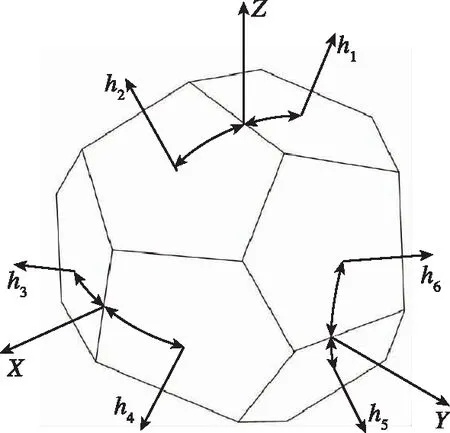
图2 传感器正十二面体配置方案Fig.2 Regular dodecahedron configuration of sensors

2.2 故障诊断过程

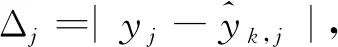
在满足2.1节3个条件下的故障检测过程如下[16-17]：

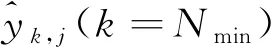
图3 故障诊断流程图Fig.3 Fault diagnosis tree

3 仿真验证

3.1 数据提取和分析

本文以6个单自由度陀螺仪安装在正12面体构成的冗余结构为例(图2)，研究单陀螺发生故障和多陀螺同时出现故障时的故障诊断问题。

仿真环境：安装误差角为15″；刻度系数误差为5×10-5；传感器常值偏置量为0.05(°)/h；量测噪声ε为0.01(°)/h。假设载体以300m/s作匀速机动，仿真时长8ks。无故障时采集陀螺测量值。由2.1节，把任意3个陀螺作为输入，另外3个陀螺作为输出，一共构建K=20个神经网络。训练时，先对样本做一些处理，首先使所有数据都分布在[-1,1]范围内，输入数据归一化和反归一化处理采用premnmx函数。利用Matlab进行仿真[12]，平滑参数σ根据不同的网络训练，选取不同的值。

3.2 分析

(1)单陀螺出现故障

假设4号陀螺在第4ks的时候出现0.5(°)/h的偏置故障。首先从所有GRNN中找到具有可疑故障陀螺数最少的GRNN。本例是由1、3、6号陀螺为输入， 2、4、5号陀螺为输出的GRNN(记为G1)，可疑故障陀螺数最少，为1个。其4号陀螺输出值(图中红色粗线)和预测值(图中蓝色细线)的比较如图4所示，4号陀螺输出值与预测值的估计残差如图5所示。

图4 4号陀螺输出值与预测值比较Fig.4 Comparison of output value and prediction value of gyro No.4

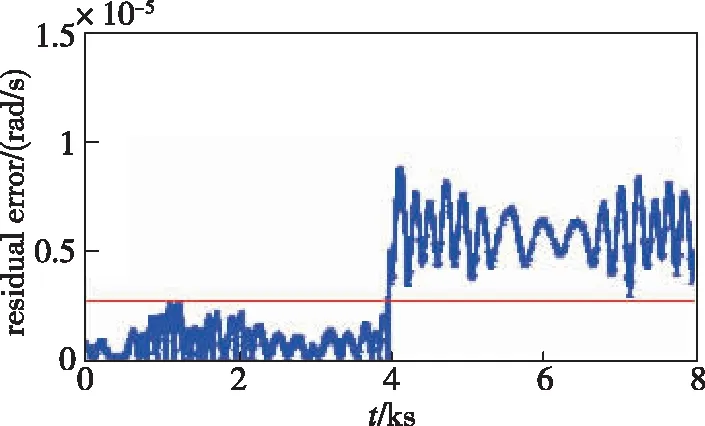
图5 4号陀螺故障检测的残差估计Fig.5 Residual estimation of gyro No.4 fault detection

由图4可以看出，训练良好的GRNN能很好地预测陀螺输出，这为故障检测创造了必要条件。当4号陀螺出现故障时，由图5可以看出，残差(蓝色粗线)超出检测门限(红色细线)；而G1的其他陀螺估计残差(图6)，都远远没有超出门限。由此判断出可疑故障陀螺为G1中的4号陀螺。

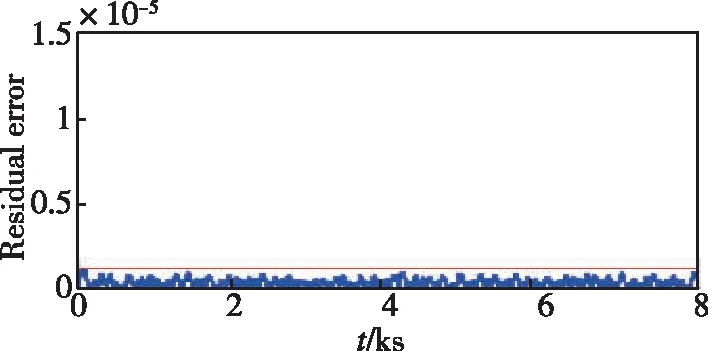
图6 G1其他陀螺的残差估计Fig.6 Residual estimation of other gyroscopes in G1

作为验证，找出一个以4号陀螺为输入的GRNN。例如找到以2、3、4号陀螺为输入，1、5、6号陀螺为输出的GRNN(记为G2)，把G1的4号陀螺估计值作为G2的4号陀螺输入，而G2的其他陀螺输入继续采用原来的值，检测G2 3个输出陀螺的残差，发现都没有超过门限，因此判断4号陀螺发生故障。

(2)多陀螺同时出现故障

本例中，假设1号陀螺在第4ks时出现0.8(°)/h的偏置故障，2号陀螺出现0.5(°)/h的偏置故障。

首先，从所有GRNN中找到具有可疑故障陀螺数最少的GRNN。本例是由3、4、5号陀螺为输入， 1、2、6号陀螺为输出的GRNN(记为G3)，可疑故障陀螺数最少，为2个。其1号陀螺输出值与预测值的估计残差如图7所示，2号陀螺输出值与预测值的估计残差如图8所示。

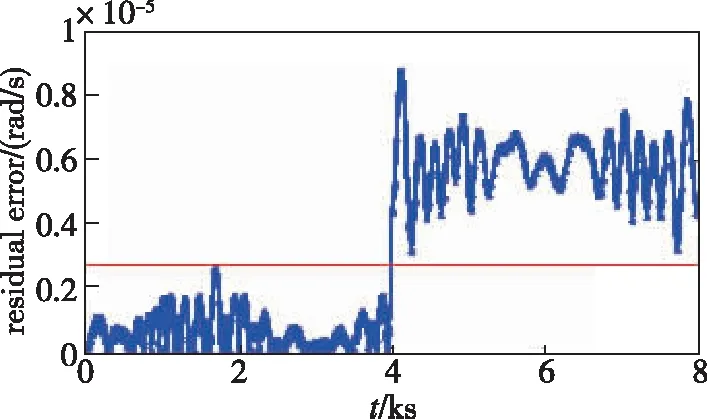
图7 1号陀螺故障检测的残差估计图Fig.7 Residual estimation of gyro No.1 fault detection

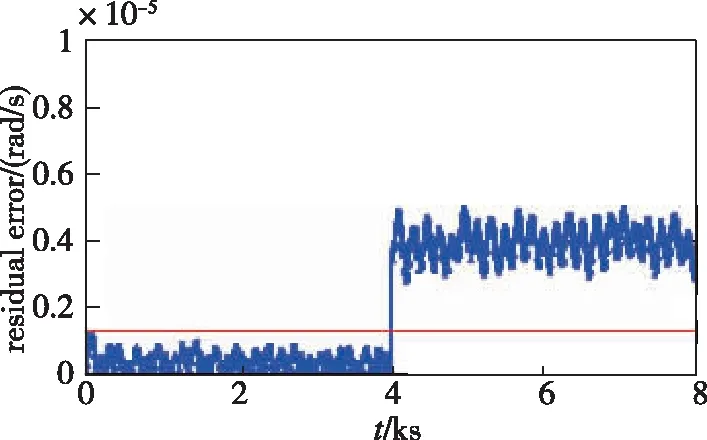
图8 2号陀螺故障检测的残差估计图Fig.8 Residual estimation of gyro No.2 fault detection

由图7和图8可以看出，1号和2号陀螺残差超出检测门限，判断可疑故障陀螺为G3中的陀螺。

作为验证，找出以1、2号陀螺为输入的GRNN。例如找到以1、2、3号陀螺为输入，4、5、6号陀螺为输出的GRNN(记为G4)，把G3的1、2号陀螺估计值作为G4的1、2号陀螺的输入，而G4的其他陀螺输入继续采用原来的值，检测G4 3个输出陀螺的残差，发现都没有超过门限，因此判断1、2号陀螺均发生了故障。