单无限马氏环境下可列齐次马氏链的一类强偏差定理
2020-09-21石志岩丁承军
石志岩,周 红,丁承军
(江苏大学数学科学学院,江苏 镇江 212013)
1 引言
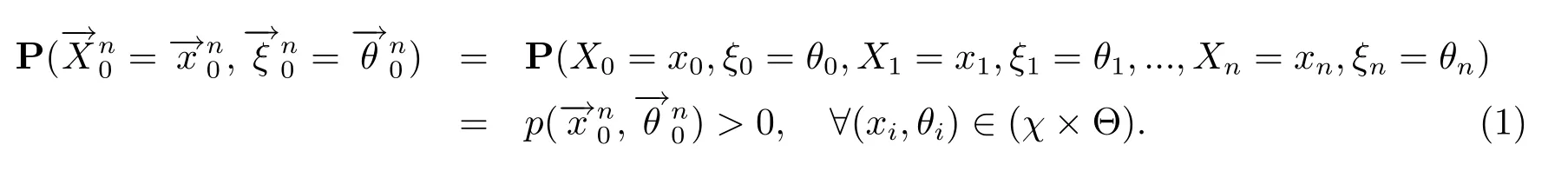
令
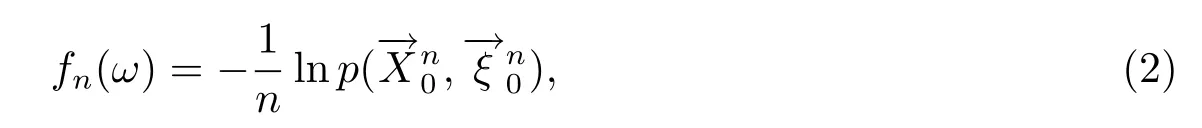
称fn(ω)为{(Xn,ξn),n≥0}的熵密度,其中ln是以e为底的自然对数.
定义 1设是定义在可测空间(Ω,F)上分别取值于Θ和χ的随机变量序列.设Q为可测空间(Ω,F)上的另一个概率测度,若对任意x,y∈χ,n∈N+,有
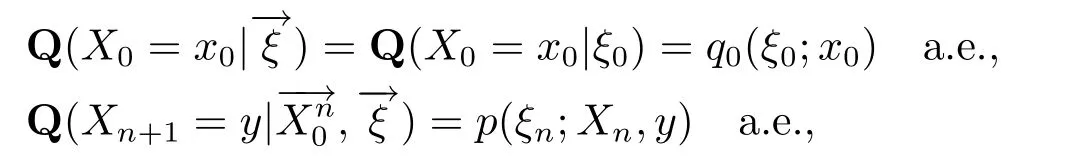
则称在概率测度Q 下为单无限随机环境下的马氏链.特别地,若是马氏链,则称在概率测度Q下为单无限马氏环境下的马氏链.
易知,若在概率测度Q 下为单无限马氏环境下的马氏链,则{(Xn,ξn),n≥0}在概率测度Q 下是马氏双链[1].特别地,若{ξn,n≥0}是初始分布为p′(θ0),转移概率为K(θ,α)的马氏链,则在概率测度Q下,{(Xn,ξn),n≥0}是一个具有初始分布

和转移矩阵
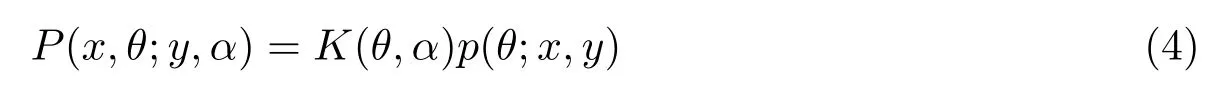
的马氏双链.设{(Xn,ξn),n≥0}在概率测度Q下的有限维分布为
在鼻胃镜可通过狭窄病变的病例中,利用鼻胃镜成功辅助完成46例消化道狭窄内镜下治疗,成功率100%。在食管癌中,行16例支架置入/调整术,2例光动力治疗;食管术后吻合口狭窄中,行5例支架置入术,2例吻合口狭窄扩张术,1例引流管置入术,1例光动力治疗术;食管外压性狭窄中,行1例支架置入术;食管不明原因性狭窄中,行1例扩张术。胃癌中,行7例支架置入术,1例肠梗阻导管置入术;胃术后吻合口狭窄中,行2例支架置入术,1例营养管置入术。结直肠癌中,行4例支架置入术,2例肠梗阻导管置入术(表6)。
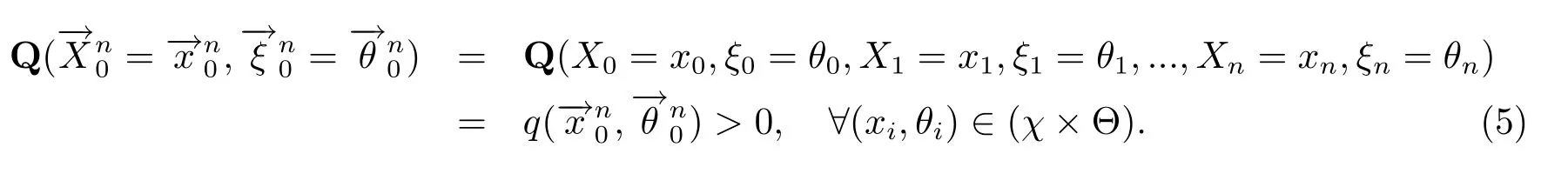
易知,若{(Xn,ξn),n≥0}在概率测度Q下为马氏环境下马氏链,则
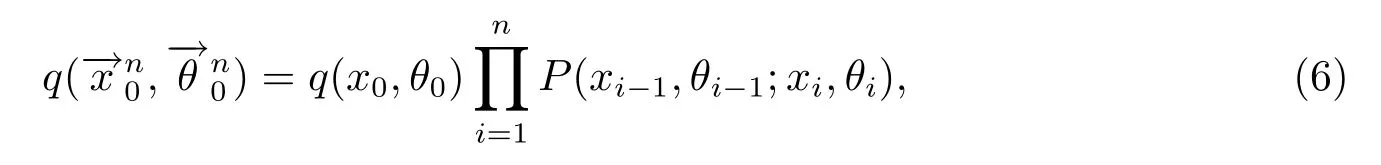
且
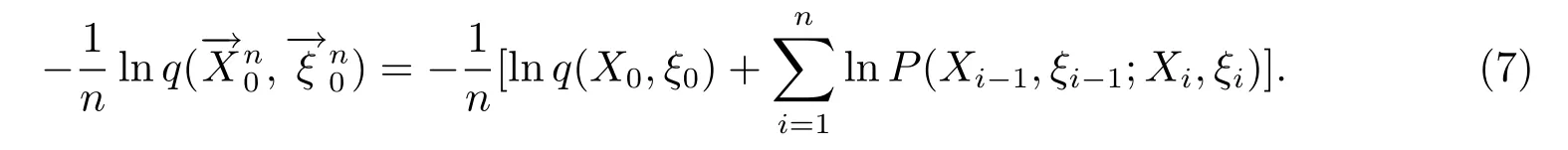
设概率测度P和Q为可测空间(Ω,F)上的概率测度,令
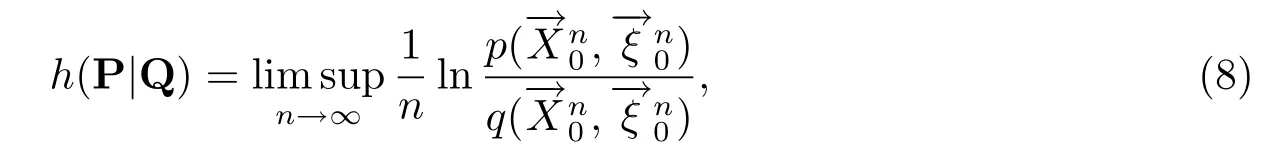
称h(P|Q)为P关于Q的渐近对数似然比.特别地,若{(Xn,ξn),n≥0}在概率测度Q下是单无限马氏环境下的马氏链,则
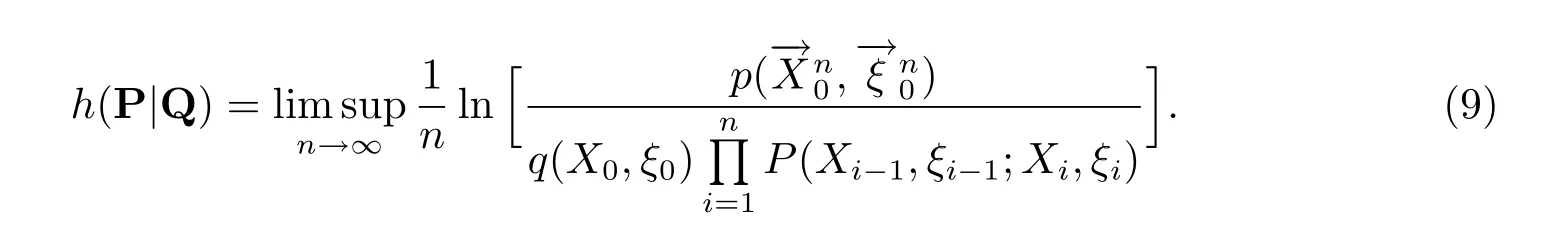
随机环境中的马氏链的研究已有相当长的历史,Nawrotzkill[2,3]建立了随机环境中的一般理论.Cogburn[1,4,5]构造了Hopf-链,利用Hopf-链理论深入研究了平稳环境中马氏链的遍历理论,中心极限定理,直接收敛和转移函数的周期性关系以及不变概率测度的存在性.Hu[6-8]对连续时间参数的随机环境中的马氏过程的存在性,等价性,q-过程的存在唯一性进行了研究.李应求等[9-11]利用鞅差理论来研究随机环境中的马氏链,在假设马氏双链遍历的条件下,得到了马氏环境中马氏链的强大数定律成立的充分条件以及马氏环境中若干强极限定理.石志岩等[12-14]研究了随机环境下树指标马氏链的定义及其存在性,以及马氏环境下Cayley树指标马氏链的Shannon-McMillan定理.
强偏差定理(亦称小偏差定理)是由不等式表示的一类强极限定理,它是强极限定理的推广.刘文和杨卫国[15]研究了马氏逼近和任意随机变量序列的一类小偏差定理;杨卫国[16]研究了任意N值随机变量序列关于m阶非齐次马氏链的一类小偏差定理;彭维才[17]研究了关于齐次树上随机场的一类强偏差定理;石志岩[18]研究了树指标随机过程的一类强偏差定理;石志岩和季金莉等[19]研究了可列齐次马氏链的一类强偏差定理.
本文首先给出渐近对数似然比的概念,通过构造非负鞅的方法,建立可列状态齐次马氏链的强偏差定理.最后,我们得到了单无限马氏环境下可列齐次马氏链的强大数定律及Shannon-McMillan定理.
2 主要结论及证明
引理1

证该引理的详细证明与文献[20]的引理1类似,故此处省略.
引理2设P和Q是定义在可测空间(Ω,F)上的两个概率测度,且{(Xn,ξn),n≥0}在概率测度Q下为定义1中定义的单无限马氏环境下的马氏链.f(x,θ;y,α)是(χ×Θ)2上的实函数,λ为一个实数.令
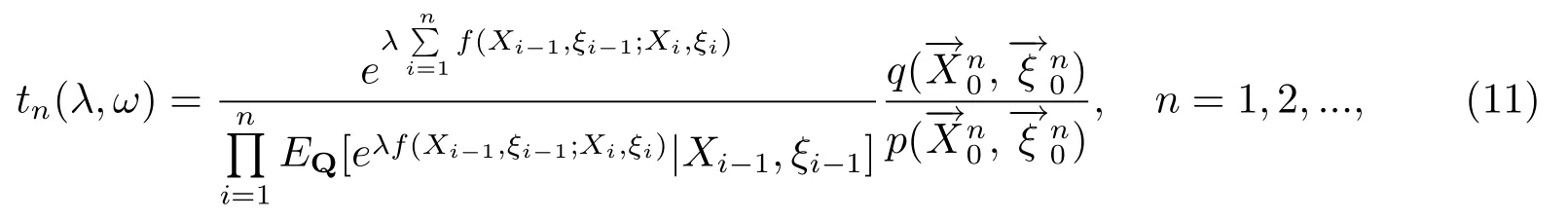
其中EQ表示在概率测度Q下的期望,则{tn(λ,ω),Fn,n≥1}是概率测度P下的非负鞅.
证令则


因此{tn(λ,ω),Fn,n≥1}是概率测度P下的非负鞅.
定理1设P和Q是定义在可测空间(Ω,F)上的两个概率测度,{(Xn,ξn),n≥0}在概率测度Q下为取值于可数状态空间(χ×Θ)的单无限马氏环境下的马氏链,f(x,θ;y,α)是定义于(χ×Θ)2上的实函数.令c≥0,

假设存在实数α>0,对任意正整数k,有
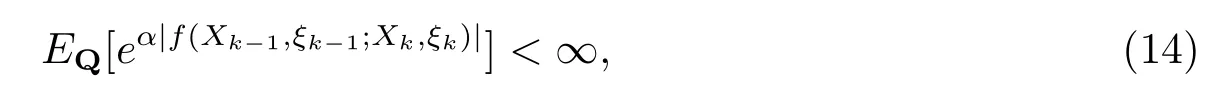
且任意(x,θ)∈(χ×Θ),有
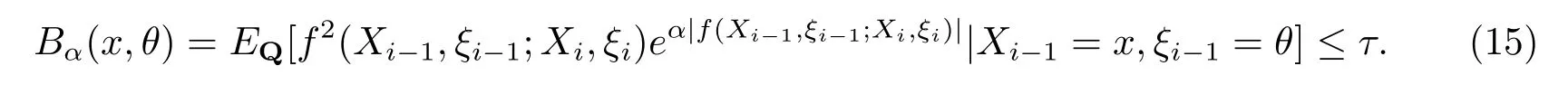
其中EQ表示在概率测度Q下的期望.则有
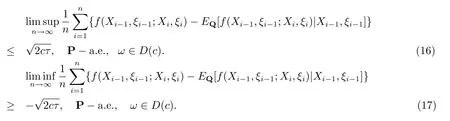
特别地
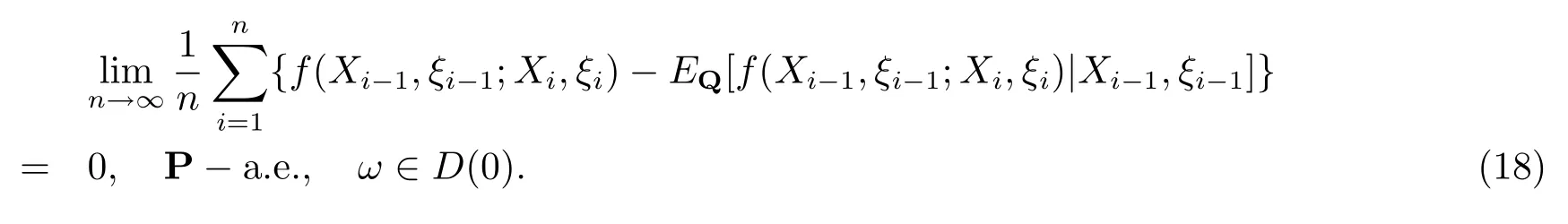
证由引理2知,{tn(λ,ω),Fn,n≥1}是在概率测度P下是非负鞅,由Doob鞅收敛定理[21]知,存在一个有限非负随机变量t∞(λ,ω)使得P-a.e.,故
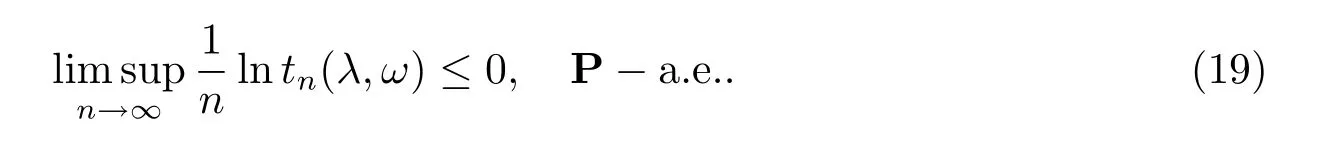
由(10)和(19)式有
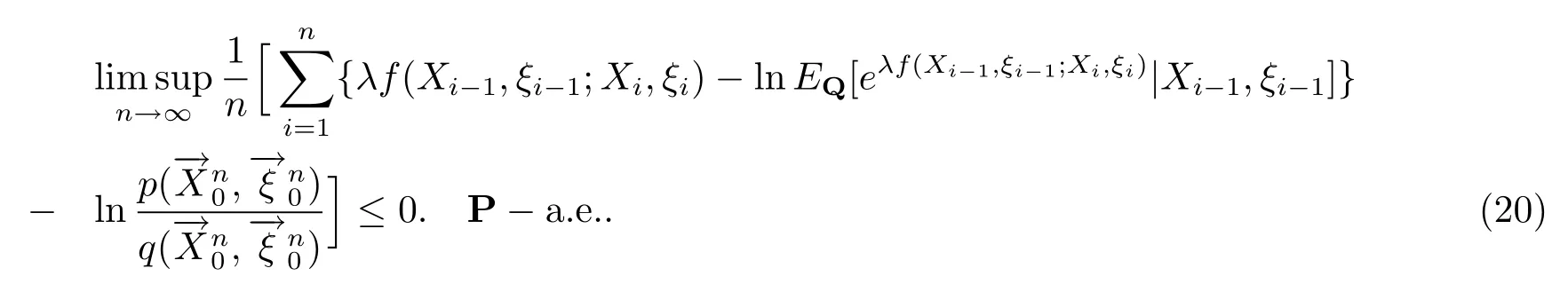






3 Shannon-McMillan定理
fn(ω)在某种意义下收敛于常数(L1收敛,依概率收敛,a.e.收敛),在信息论中称为Shannon-McMillan定理或熵定理或称为信源的渐近等分性(AEP).Shannon[22]首先研究了有限字母集上的平稳遍历信源依概率收敛的渐近等分性;McMillan[23]和Breiman[24]分别证明有限字母集上的平稳遍历信源L1收敛和a.e.收敛的渐近等分性;钟开莱[25]研究了字母集为可列的情况;刘文和杨卫国[26,27]给出了一类非齐次马氏信源的渐近等分性以及m阶非齐次马氏信源的渐近等分性.本节我们将研究单无限马氏环境下可列齐次马氏链的Shannon-McMillan定理.
定理3设{(Xn,ξn),n≥0}是取值于可数状态空间(χ×Θ)的随机变量序列.设P是强遍历的,且π是由P决定的唯一平稳分布.若
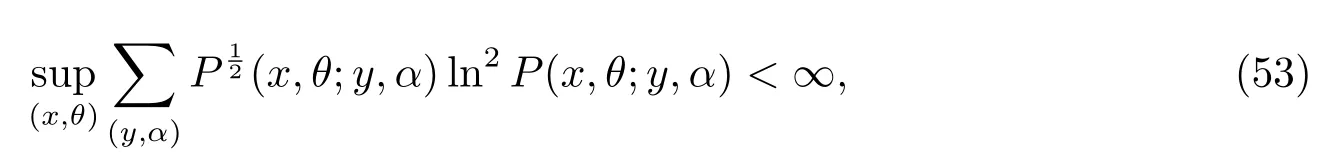

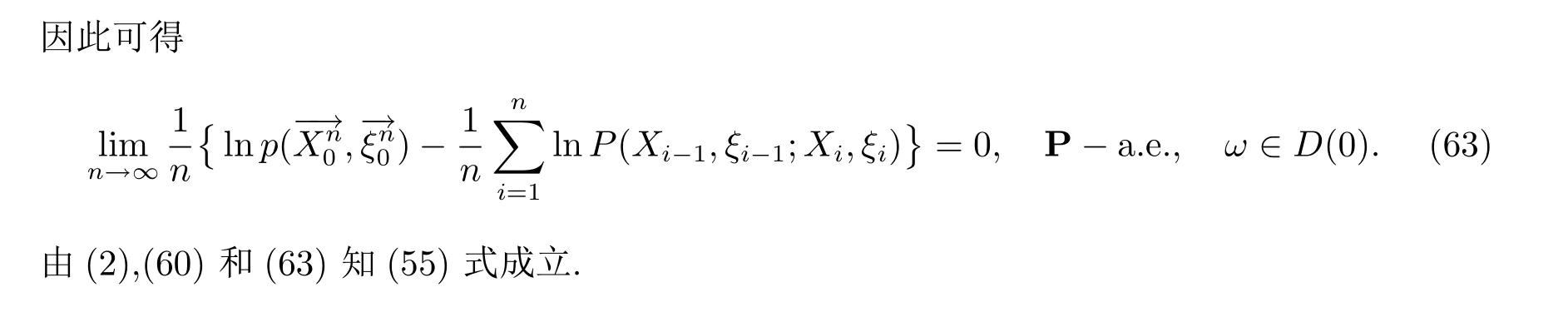
附录
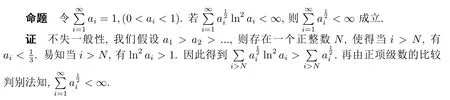
猜你喜欢
杂志排行
数学杂志的其它文章
- HYPOELLIPTIC ESTIMATE FOR SOME COMPLEX VECTOR FIELDS
- FAST AND SLOW DECAY SOLUTIONS FOR SUPERCRITICAL FRACTIONAL ELLIPTIC PROBLEMS IN EXTERIOR DOMAINS
- NORM STRUCTURES OF A FUZZY NORMED SPACE
- MODIFIED LAVRENTIEV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OFHELMHOLTZ-TYPE EQUATION
- BIFURCATION AND POSITIVE SOLUTIONS OF A p-LAPLACIAN PROBLEM
- 几类区域上不等维的边界唯一性定理
