温室穴盘苗自动移钵路径优化
2020-09-20张丽娜吕昊暾李宝胜蒋易宇
张丽娜,谭 彧,吕昊暾,李宝胜,蒋易宇,王 硕
温室穴盘苗自动移钵路径优化
张丽娜,谭 彧,吕昊暾※,李宝胜,蒋易宇,王 硕
(中国农业大学工学院,北京 100083)
为了优化移栽机补栽作业时的移钵路径,该研究基于免疫算法构建了克隆选择算法和免疫遗传算法2种适合求解移钵路径优化问题的模型,并与固定顺序法和遗传算法对比,进行移钵路径规划仿真试验和验证试验。结果表明:克隆选择算法模型和免疫遗传算法模型均能有效优化移钵路径,免疫遗传算法模型的路径规划效率较高,而克隆选择算法模型的路径规划效率较低。验证试验条件下,该研究2种模型的路径规划长度分别为48 977和48 945 mm,相比固定顺序法分别缩短7.59%和7.65%,相比遗传算法模型分别缩短3.60%和3.66%;2种模型的计算时间分别为5.86和2.72 s,免疫遗传算法模型的计算时间相对遗传算法减少15.79%。免疫遗传算法模型可作为温室穴盘苗后续机械化批量补栽的路径规划控制基础。
温室;穴盘苗;优化;自动移栽;路径规划;克隆选择算法;免疫遗传算法
0 引 言
温室穴盘育苗技术改变了传统生产方式和种植制度,提高了经济效益,已被广泛应用[1-5]。在工厂机械化育苗生产中,成苗率约为80%~95%[6]。其中播种机漏播、种子未发芽以及畸形苗统称为劣质钵苗。针对穴盘中的劣质钵苗,需进行剔除,并对其进行健康钵苗补栽作业,否则会导致后续机械化批量移栽时出现栽空或漏栽。钵苗移栽机器人对劣质钵苗进行剔除后,需逐一抓取移栽穴盘内的健康钵苗进行补栽,移钵路径(即补栽路径)具有多选择性,对移钵路径进行优化能够有效降低末端执行器的行走距离,提高工作效率。
童俊华等[6-7]采用遗传算法对穴盘苗移钵路径进行优化,但对于穴盘穴孔数目较多的情况,该算法计算时间较长[7],规划效果有待提高。此后童俊华等[7]又采用贪心算法对移栽路径进行优化。贺磊盈等[8-9]采用贪心遗传算法对穴盘苗移钵路径进行近似最优规划,相比于固定顺序法,路径规划长度有所降低。徐守江等[10-11]基于蚁群算法和混合蛙跳算法对穴盘苗移钵路径进行优化。虽然已有部分学者对穴盘苗移钵路径进行了研究,但路径规划效果仍有待进一步提高。
温室穴盘苗移钵路径优化问题类似于旅行商问题(Traveling Saleman Problem,TSP),免疫算法被广泛用于解决TSP问题[12-13]。本文借鉴免疫算法求解TSP问题的思路,分别基于免疫克隆选择算法(Clonal Selection Algorithm,CSA)和免疫遗传算法(Immune Genetic Algorithm,IGA),构建了2种适于求解穴盘苗移钵路径优化问题的模型,并进行仿真试验和实际验证试验,以确定最佳的路径优化模型,为后续温室穴盘苗的机械化批量补栽提供路径规划控制基础。
1 移钵作业过程
钵苗自动移栽机主要由穴盘苗输送系统、机器视觉识别系统、控制系统、移钵系统组成,如图1所示,通过4个系统的协同作业依次完成劣质钵苗的识别与定位、劣质钵苗剔除和健康钵苗补栽作业[14-18]。

1.穴盘苗输送系统 2.机器视觉识别系统 3.控制系统 4.移钵系统
常用的穴盘尺寸为250 mm×500 mm,规格以穴孔数量(其中=50、72、128)定义[6]。图2是一个50穴孔规格的穴盘(下文简称50穴孔穴盘)示意图,目的穴盘中的空穴代表需要补栽的位置;移栽穴盘中的健康钵苗用于补栽作业。移钵路径优化即是对移栽穴盘中的健康钵苗进行选取,然后确定补栽顺序,以保证移栽机械臂的运动路径最短。

图2 50穴孔穴盘示意图
目前工程上主要采用固定顺序法[7](Common Sequence Method,CSM)进行移钵作业,从移栽穴盘中按从上往下、从左至右的顺序取苗,再将钵苗按从上至下、从右至左的顺序移入到目的穴盘的空穴中去,而不对移钵路径进行比较选择。
目的穴盘中劣质钵苗是随机分布的,剔除后的空穴需要进行补栽。移栽穴盘中健康钵苗具有多选择性,因此,移栽穴盘中健康钵苗向目的穴盘中的空穴补栽时,存在多种移钵路径。假设移栽穴盘内可供移栽的健康钵苗为1株,目的穴盘中需随机补栽的空穴为2个(1≤2≤1≤),此时可供选择的移钵路径共有(1!×2!)/(1-2)! 种,移栽机械臂在不同路径下的运动距离不同,移钵距离越短工作效率越高,因此有必要寻求一条最短距离的移钵路径。若采用普通的遍历方法[6]寻求最短路径,对计算机的运行速度和内存要求很高,普通计算机难以满足要求,有必要设计一种更合理的求解最优移钵路径的方法。
2 移钵路径优化模型构建
免疫算法[19-20]是基于生物免疫系统识别抗原并产生抗体对抗抗原的学习机制提出的智能算法,本文基于免疫算法原理构建出了2种移钵路径优化求解的免疫算法模型:克隆选择算法模型和免疫遗传算法模型。
2.1 基于克隆选择算法的移钵路径优化模型
克隆选择算法(Clone Selection Algorithm,CSA)是一种基于免疫系统的克隆选择原理形成的搜索算法,具有较强的全局搜索能力[21-22]。针对移钵路径优化,设计克隆选择算法模型的实现过程如下:
1)识别待优化问题及约束条件。移钵路径优化问题可以描述为:从原点出发,选取移栽穴盘中健康钵苗,依次对目的穴盘中的空穴进行补栽,补栽完成后回到原点,要求移钵路径距离最短,且应保证目的穴盘中的空穴被全部补栽,移栽穴盘中的每株健康钵苗能且只能被移栽1次,移栽总量与目的穴盘中空穴数目相等。
2)随机生成抗体群,抗体规模为个,每个抗体各对应一种可行路径。抗体基因即路径编码采用实数编码的形式,编码长度length取决于目的穴盘中待补钵苗的数量2,即length=2×2,参考文献[6]的编码方式,按照从左至右、从下至上的顺序对目的穴盘中的空穴和移栽穴盘中的健康钵苗依次进行编码,如1=36、2=4,则其中一个抗体的编码可表示为(4, −1, 9, −3, 12, −4, 36, −2)。
3)抗体与抗原之间的亲和度应能反应抗体与抗原的匹配程度,本文针对移钵路径优化设计抗体与抗原之间的亲和度函数fit()如公式(1)所示。

其中len()代表第个抗体的路径总长,mm。
4)定义亲和度最大的/2个抗体为成功识别抗原的抗体,选择这部分抗体作为克隆源依次进行克隆,每个抗体克隆个;以公式(1)计算出的亲和度为依据,按照轮盘赌选择法对克隆体进行变异操作,生成新的移钵路径。
5)比较克隆源与变异抗体的亲和度,仅保留亲和度最高的抗体(即移钵路径最短的抗体)进入新的抗体种群;克隆抑制后种群个数减少为/2个,为了增加抗体的多样性,扩大搜索范围,继续随机生成/2个新的抗体,与克隆抑制后的抗体合并形成新的抗体群。
该模型的实现流程如图3所示。

图3 克隆选择算法模型流程图
2.2 基于免疫遗传算法的移钵路径优化模型
Wang等[23-25]将免疫算子引入遗传算法中,提出了一种免疫遗传算法,解决了遗传算法的早熟收敛问题,具有较强的寻优能力。本文针对移钵路径优化,设计免疫遗传算法模型的实现过程如下:
1)随机生成抗体群,该抗体群由普通抗体和记忆细胞组成,抗体规模为个,其中普通抗体规模为1个,记忆细胞规模为2个。模型初始化时,记忆细胞库中的抗体与普通抗体相同,都通过随机方式产生。
2)计算抗体的期望繁殖率。每个抗体的期望繁殖率exc()由抗体与抗原的亲和度fit()和抗体的浓度con()共同决定[26]:

式中ps为多样性评价参数,常取为0.95[27]。
进行抗体浓度计算的前提是计算抗体与抗体之间的亲和度,免疫遗传算法中常用基于海明距离的计算方法、基于信息熵的计算方法和基于欧式距离的计算方法,但以上3种方法均存在计算量大、路径规划效率低的问题[28],且不适用于移钵路径优化问题。
本文对抗体与抗体间亲和度计算方法进行改进,采用位连续法[29]设计抗体间的亲和度S计算函数,如公式(3)所示。

式中length为抗体编码长度,R为抗体与抗体的路径编码的最长公共基因个数。
例如,3个抗体的路径编码分别为(4, −1, 9, −3, 12, −4, 26, −2)、(4, −1, 9, −2, 7, −4, 8, −3)和(36, −2, 6, −3, 12, −4, 8, −1),则抗体1与抗体2、抗体1与抗体3、抗体2与抗体3的最长公共基因个数分别为3个(4, −1, 9和4, −1, 9)、3个(−3, 12, −4和−3, 12, −4)、和2个(−4, 8和−4, 8),其亲和度12、13、23分别为0.375、0.375和0.25。
当2个抗体的亲和度高于某个阈值,即2个路径编码的最长公共基因个数与编码长度的比值高于某个阈值时,认为2个抗体相似。若抗体与抗体相似,则抗体必与抗体相似,故抗体相似具有对称性。基于此,本文采用一种基于相似浓度矩阵的抗体浓度计算方法[30],可有效减少计算量,其具体方法为:
定义一个大小为×的相似浓度矩阵,C代表抗体和抗体的相似度,C为1则代表抗体和抗体相似,为0则不相似,如公式(4);相似浓度矩阵的第行表示抗体与群体中所有抗体(包括自身)的相似关系,抗体的浓度con()可通过公式(5)计算得到。由于抗体相似具有对称性,因此C=C=1。

式中为预先设定的一个阈值,本文设计为一个变量,与抗体编码长度有关,由公式(6)计算得到。

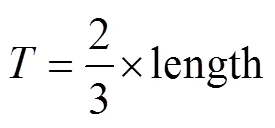
分析可知,对于的2个元素来说,只需计算(−1)/2个元素就可完成的计算,即抗体浓度的计算量减少,算法的运行速度提高。
3)保留精英路径。为了避免与抗原亲和度最高的抗体因其浓度高受到抑制,导致最优解丢失,采用精英保留策略,选取与抗原亲和度最高的个抗体放入记忆细胞库。然后按照抗体的期望繁殖率,选取(2−)个抗体放入记忆细胞库。
4)以式(2)计算出的期望繁殖率为依据,采用轮盘赌选择法对抗体进行单点交叉和变异操作,并针对移钵路径的特殊性进行去重和替换操作[6],得到新抗体;新抗体与记忆库中的精英抗体合并,形成新种群。
该模型的实现流程如图4所示。
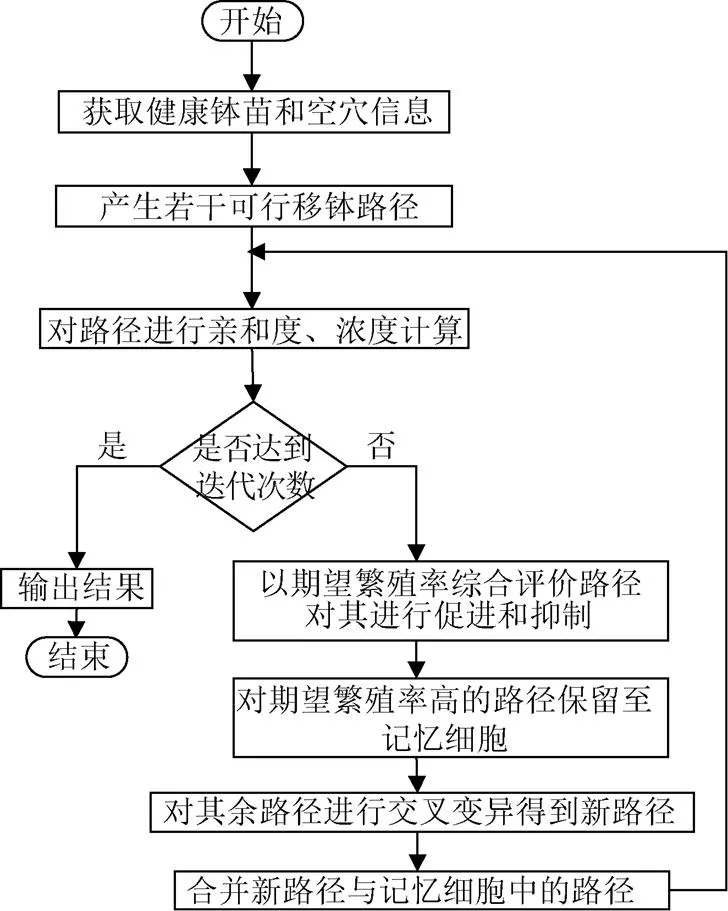
图4 免疫遗传算法模型流程图
3 仿真试验与结果分析
为了测试本文设计的2种优化模型的有效性和工作性能,进行移钵路径规划仿真试验,仿真环境为MATLAB R2013b。通过预试验对一些关键参数进行确定,设定克隆选择算法模型中种群规模为40,迭代次数为50,变异概率为0.4,克隆个数为10个;免疫遗传算法模型中种群总规模为40(其中记忆细胞库容量为10个),迭代次数为50,交叉概率为0.5,变异概率为0.4,参考文献[27],多样性评价参数为0.95。参考文献[6],移栽穴盘和目的穴盘的间距设定为100 mm。
3.1 试验方案
3.1.1 有效性验证试验
为验证本文设计的2种优化模型的有效性,以文献[6]、文献[10]和文献[11]中的1组经典移钵实例进行路径规划对比试验,目的穴盘和移栽穴盘均为50穴孔穴盘,目的穴盘中劣质钵苗的数量为4株,移栽穴盘中健康钵苗的数量为36株,目的穴盘和移栽穴盘中钵苗分布如图5a所示。文献[6]、文献[10]和文献[11]分别采用遗传算法、蚁群算法和蛙跳算法。
3.1.2 随机对比试验
为了进一步对比本文所设计2种模型与其他经典算法之间的优劣性,选择固定顺序法(Common Sequence Method,CSM)和遗传算法(Genetic Algorithm,GA),以路径规划长度和计算时间为指标展开对比试验,其中遗传算法是指文献[6]所用算法。遗传算法涉及路径优化和计算时间,而固定顺序法作为最基本的移钵方法,对于确定的移钵情况,其路径是固定的,无需计算,不涉及计算时间,因此在进行试验结果对比时,固定顺序法只参与路径规划长度对比,不参与计算时间对比。
穴盘苗补栽时,移栽穴盘和目的穴盘中的劣质钵苗数量(空穴数)是随机的,在穴盘规格的5%~20%范围内[6],位置也是随机分布在穴盘中的。选取50、72和128穴孔穴盘进行移钵路径规划仿真试验,目的穴盘和移栽穴盘的规格一致,移钵数量人为设置,位置随机,以移栽穴盘内健康钵苗全部移完为1组试验,1个移栽穴盘约向5~10个目的穴盘进行补栽,各组试验中均进行多次路径规划,将多次路径规划长度和计算时间累加作为各组试验的结果。3种规格的穴盘分别进行5组试验,每组试验的移钵数量如表1所示。如表1所示,50穴孔穴盘的第1组试验中,移栽穴盘中健康钵苗的数量为41株,共向5个目的穴盘进行了补栽;50穴孔穴盘的第2组试验中,移栽穴盘中健康钵苗的数量为43株,共向6个目的穴盘进行了补栽。
因128穴孔穴盘含钵苗数量多,计算量大,迭代次数为50时2种优化模型的收敛曲线不平稳,路径规划长度仍有较大优化空间,故本试验中将迭代次数设置为80。

表1 随机对比试验的移钵数量
注:“-”表示移栽穴盘中健康钵苗已被移完,目的穴盘补栽结束。
Note: “-” means that all healthy seedlings in transplant tray had been transplanted, and objective plug tray replanting had been done.
3.2 仿真试验结果与分析
3.2.1 有效性验证试验结果与分析
表2为有效性验证试验结果。由表2可知,2种模型得到的最优路径长度均为2 914 mm,略优于遗传算法,与蚁群算法和蛙跳算法的规划效果一致;克隆选择算法、免疫遗传算法、遗传算法和蚁群算法的平均计算时间分别为0.61、0.24、0.65和0.54 s,克隆选择算法与遗传算法的计算时间相近,免疫遗传算法明显优于遗传算法和蚁群算法,且优于基于克隆选择算法,表明本文所设计的2种模型均能有效完成路径规划,且路径规划效果较好。图5为本文设计的2种优化模型的路径规划结果和收敛曲线,由图5可知,在该组试验中,本文所设计的2种模型均能在50代内快速收敛,规划的路径长度较稳定,表明2种模型性能稳定。

表2 不同算法下经典移钵实例的仿真结果对比
注:CSM指固定顺序法,GA指文献[6]的遗传算法,ACO指文献[10]的蚁群算法,SFLA指文献[11]的蛙跳算法,CSA指本文的克隆选择算法,IGA指本文的免疫遗传算法,“*”指文献中无此数据。
Note: CSM refers to the Common Sequence Method, GA refers to the Genetic Algorithm used in literature[6], ACO refers to the Ant Colony Algorithm used in literature[10], SFLA refers to the Leapfrog Algorithm used in literature[11], CSA refers to the Clone Selection Algorithm model designed in this paper, IGA refers to the Immune Genetic Algorithm model designed in this paper, “*” refers to the data not mentioned in the literatures.
3.2.2 随机对比试验结果与分析
图6为50、72和128穴孔穴盘仿真试验的路径规划长度对比。由图6可知,在3种规格穴盘的各组试验中,克隆选择算法模型和免疫遗传算法模型路径规划长度相近,相比于固定顺序法和遗传算法模型明显缩短。根据试验结果,进一步计算得到固定顺序法、遗传算法模型、克隆选择算法模型和免疫遗传算法模型在50穴孔穴盘仿真试验的路径规划长度总计分别为191 843、179 910、174 750和174 755 mm,在72穴孔穴盘仿真试验的路径规划长度总计分别为265 065、249 880、241 433和243 419 mm,128穴孔穴盘仿真试验的路径规划长度总计分别为460 623、436 155、416 053和416 310 mm。对比可知,在3种规格的穴盘仿真试验中,各算法模型按照路径规划长度从小到大的顺序均为:克隆选择算法模型、免疫遗传算法模型、遗传算法模型、固定顺序法,其中本文设计的2种模型的路径规划长度相近,相比于另外2个模型明显缩短,尤其是128穴孔穴盘,克隆选择算法模型和免疫遗传算法模型相比固定顺序法分别最大可缩短9.68%和9.62%,相比遗传算法模型分别最大可缩短4.61%和4.55%。
固定顺序法并未对移钵路径进行比较选择,故路径长度最长;遗传算法对特征信息利用不足,新生成的子代个体路径编码可能发生突变,性能劣于父代个体,因此移钵路径优化效果差;克隆选择算法的克隆选择和克隆抑制操作,保证了迭代过程是趋于向更短移钵路径收敛的方向进行的,故具有较好的路径优化能力;免疫遗传算法模型将移钵路径最短的抗体保留至记忆细胞库,也保证了迭代是趋于向更短移钵路径收敛的方向进行的,且对路径的产生进行促进或抑制操作,保证了抗体路径编码的多样性,避免了局部收敛,因此也具有较好的路径优化能力。

图5 经典移钵实例的仿真结果及对比

图6 不同规格穴盘仿真试验的规划路径长度对比
图7为50、72和128穴孔穴盘仿真试验的路径规划计算时间对比。由图7可知,在3种规格穴盘的各组试验中,相比于遗传算法模型,免疫遗传算法模型的计算时间明显减少,但克隆选择算法模型的计算时间却增加,免疫遗传算法模型路径规划效率较高。根据试验结果,进一步计算得到遗传算法模型、克隆选择算法模型和免疫遗传算法模型在50穴孔穴盘仿真试验的计算时间总计分别为11.89、21.48和9.42 s,在72穴孔穴盘仿真试验的计算时间总计分别为15.64、27.93和12.13 s,128穴孔穴盘仿真试验的计算时间总计分别为48.27、84.00和34.04 s。对比可知,在3种规格穴盘仿真试验中,3种算法模型按照计算时间从小到大的顺序为:免疫遗传算法模型、遗传算法模型、克隆选择算法模型,本文设计的免疫遗传算法模型的计算时间相比遗传算法明显减少,尤其是128穴孔穴盘,最大可减少29.48%,但克隆选择算法模型的计算时间最长,路径规划效率比免疫遗传算法模型低。

图7 不同规格穴盘仿真试验的计算时间对比
本文在设计免疫遗传算法模型时引用相似浓度矩阵的方式计算抗体浓度,避免了许多重复性的计算,因此能够有效减少计算时间;克隆选择算法模型的克隆复制和克隆抑制操作,相比于免疫遗传算法和遗传算法模型增大了计算量,故计算时间长。
仿真试验表明:相比固定顺序法和遗传算法,本文设计的克隆选择算法模型和免疫遗传算法模型均具有较好的移钵路径优化能力,但免疫遗传算法模型的路径规划效率更高。
4 验证试验
为了验证本文设计的2种模型的实际工作效果,进一步基于克隆选择算法模型、免疫遗传算法模型、固定顺序法、遗传算法模型开展实际验证试验。钵苗移栽机和移栽穴盘如图8所示,移栽穴盘中劣质钵苗共有7株,位置见图8b。本文以中农富通公司培育的中华大椒苗开展补栽试验,苗龄为20 d,穴盘规格为72穴孔,长500 mm,宽250 mm。为避免环境光线对识别效果的影响,对钵苗移栽机的机器视觉识别系统进行遮光处理,将移栽穴盘摆放在移栽穴盘固定台上,移栽穴盘和目的穴盘的间距为100 mm。
选取9个穴盘,1个作为移栽穴盘,8个作为目的穴盘,试验前将穴盘中的劣质钵苗剔除,移栽穴盘中的空穴数为7个,目的穴盘每盘的移钵数量如表3所示。试验时,首先由机器视觉识别系统获取移栽穴盘中钵苗的坐标,然后将此穴盘摆放在移栽穴盘固定台上;目的穴盘在穴盘苗输送系统的带动下,经过机器视觉识别系统下方,获取该穴盘中钵苗的坐标后停留在移栽穴盘旁边;机器视觉识别系统将获取的钵苗坐标提供给控制系统,控制系统依次利用3个算法模型进行路径规划,并控制移钵系统进行补栽作业;依次对8个目的穴盘进行补栽,试验时记录每次路径规划长度和计算时间;根据预试验,设定移钵系统的移动速度为100 mm/s,移栽机械手下降取苗和上升的时间各为1 s(此时移栽机的工作效果较稳定)。记录每个目的穴盘补栽完成所需的时间(简称补栽时间),试验结果如表3所示。

1.穴盘苗输送系统 2.机器视觉识别系统 3.移栽穴盘固定台 4.移钵系统
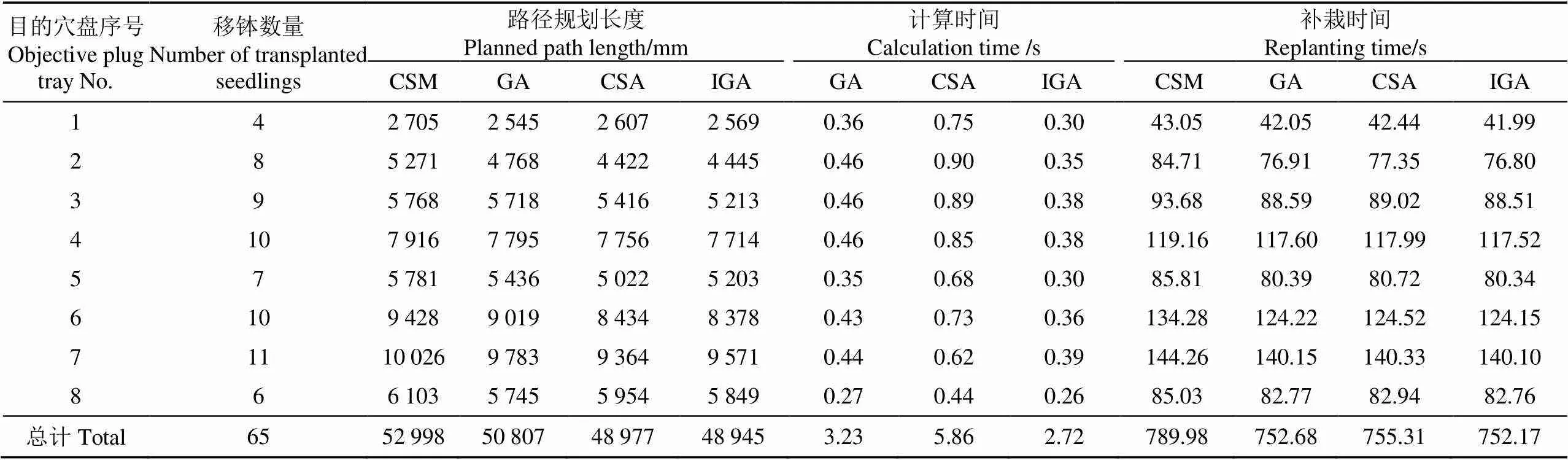
表3 不同算法下穴盘苗补栽结果对比
由表3可知,固定顺序法、遗传算法模型、克隆选择算法模型和免疫遗传算法模型的路径规划长度总计分别为52 998、50 807、48 977和48 945 mm,4种方法的路径规划长度,从小到大的顺序为:免疫遗传算法模型、克隆选择算法模型、遗传算法模型、固定顺序法,其中,免疫遗传算法模型和克隆选择算法模型的路径规划长度相近,相比固定顺序法分别缩短7.65%和7.59%,相比遗传算法模型分别缩短3.66%和3.60%。遗传算法模型、克隆选择算法模型和免疫遗传算法模型的计算时间分别为3.23、5.86和2.72 s,免疫遗传算法模型的计算时间相对遗传算法减少15.79%,克隆选择算法模型的计算时间最长,路径规划效率较低。8个目的穴盘总计补栽65株健康钵苗,固定顺序法、遗传算法模型、克隆选择算法模型和免疫遗传算法模型的补栽时间总计分别为789.98、752.68、755.31和752.17 s,4种方法的补栽时间,从小到大的顺序为:免疫遗传算法模型、遗传算法模型、克隆选择算法模型、固定顺序法,固定顺序法虽然无需计算时间,但是其路径规划长度最大,移栽机械手的执行时间最长,导致移栽时间最长。使用免疫遗传算法模型时,计算时间总计仅为2.72 s,路径规划效率较高。验证试验表明:本文设计的2种模型的实际工作效果与仿真试验结果基本一致,免疫遗传算法模型具有较好的移钵路径优化能力,且路径规划效率更高。
本文进行补栽试验时,设置移栽穴盘和目的穴盘的规格一致,在实际应用中,存在移栽穴盘和目的穴盘的规格不一致的情况,本文设计的2种模型均可适用于这种情况,只需要钵苗移栽机的机器视觉识别系统分别获取移栽穴盘和目的穴盘中钵苗的坐标,控制系统即可利用本文设计的模型进行路径规划。
5 结 论
为了改善移栽机进行钵苗补栽时的路径规划效果,本文基于免疫算法设计了克隆选择算法和免疫遗传算法2种适合求解移钵路径优化问题的模型,以固定顺序法和遗传算法为对比对象,选取50、72和128穴孔穴盘进行移钵路径规划仿真试验,并选取72穴孔穴盘进行实际验证试验,得到如下主要结论:
1)本文设计的克隆选择算法模型和免疫遗传算法模型均能有效优化移钵路径,该2种模型路径规划长度相近,相比于固定顺序法和遗传算法模型明显缩短,实际验证试验中1个移栽穴盘向8个目的穴盘进行了实际补栽,固定顺序法、遗传算法模型、克隆选择算法模型和免疫遗传算法模型的路径规划长度分别为52 998、50 807、48 977和48 945 mm,克隆选择算法模型和免疫遗传算法模型相比固定顺序法分别缩短7.59%和7.65%,相比遗传算法模型分别缩短3.60%和3.66%。
2)免疫遗传算法模型具有较高的路径规划效率,而克隆选择算法模型的路径规划效率较低。实际验证试验中,遗传算法模型、克隆选择算法模型和免疫遗传算法模型的计算时间分别为3.23、5.86和2.72 s,免疫遗传算法模型的计算时间相对遗传算法减少15.79%。
本文设计的免疫遗传算法模型不仅能有效优化移钵路径,而且规划效率更高,可作为后续温室穴盘苗机械化批量补栽的路径规划控制基础。本文仿真和实际试验中均以同规格的穴盘苗为补栽对象,对于其他规格的温室穴盘苗移钵路径优化,使用本文模型时,只需根据实际需要传入钵苗的坐标即可。
[1] 李其昀. 机械化育苗移栽的现状与展望[J]. 农机化研究,2006,28(3):26-27.
Li Qiyun. The present status and development tendency of bowl-rear transplanting mechanization[J]. Journal of Agricultural Mechanization Research, 2006, 28(3): 26-27. (in Chinese with English abstract)
[2] Ryu K H, Kim G, Han J S. Development of a robotic transplanter for bedding plants[J]. Journal of Agricultural Engineering Research, 2001, 78(2): 141-146.
[3] 张丽华,邱立春,田素博. 穴盘苗自动移栽机的研究进展[J]. 农业科技与装备,2009,185(5):28-31.
Zhang Lihua, Qiu Lichun, Tian Subo. Progress in the research of manipulator of transplanting potted tray seedlings[J]. Agricultural Science & Technology and Equipment, 2009, 185(5): 28-31. (in Chinese with English abstract)
[4] 冯青春,王秀,姜凯,等. 花卉幼苗自动移栽机关键部件设计与试验[J]. 农业工程学报,2013,29(6):21-27. Feng Qingchun, Wang Xiu, Jiang Kai, et al. Design and test of key parts on automatic transplanter for flower seedling[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(6): 21-27. (in Chinese with English abstract)
[5] 张振国,曹卫彬,王侨,等. 穴盘苗自动移栽机的发展现状与展望[J]. 农机化研究,2013,35(5):237-241.
Zhang Zhenguo, Cao Weibin, Wang Qiao, et al. Development status and prospect of plug seedlings automatic transplanting machine[J]. Journal of Agricultural Mechanization Research, 2013, 35(5): 237-241. (in Chinese with English abstract)
[6] 童俊华,蒋焕煜,周鸣川. 基于遗传算法的穴盘苗自动移钵路径优化[J]. 农业机械学报,2013,44(4):45-49,26.
Tong Junhua, Jiang Huanyu, Zhou Mingchuan. Optimization of seedling transplanting path based on genetic algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 45-49, 26. (in Chinese with English abstract)
[7] 童俊华,蒋焕煜,武传宇. 基于贪心算法的温室钵苗稀植移栽路径优化[J]. 农业机械学报,2016,47(3):8-13.
Tong Junhua, Jiang Huanyu, Wu Chuanyu. Optimization of seedlings lower density transplanting path based on greedy algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 8-13. (in Chinese with English abstract)
[8] 贺磊盈,杨太玮,武传宇,等. 基于贪心遗传算法的穴盘苗补栽路径优化[J]. 农业机械学报,2017,48(5):36-43.
He Leiying, Yang Taiwei, Wu Chuanyu, et al. Optimization of replugging tour planning based on greedy genetic algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(5): 36-43. (in Chinese with English abstract)
[9] Tong Junhua, Wu Chuanyu, Jiang Huanyu, et al. Optimizing the path of seedling low-density transplanting by using greedy genetic algorithm[J]. Computers and Electronics in Agriculture, 2017, 142(A): 356-368.
[10] 徐守江. 基于蚁群算法的穴盘苗自动移钵路径优化[J]. 江苏农业科学,2015,43(12):475-477.
[11] 徐守江,罗竹青. 基于邻域搜索的穴盘苗移钵路径优化蛙跳算法[J]. 农机化研究,2018,40(11):208-212.
Xu Shoujiang, Luo Zhuqing. Shuffled frog leaping algorithm for seedling transplanting path optimization based on neighbor search strategy[J]. Journal of Agricultural Mechanization Research, 2018, 40(11): 208-212. (in Chinese with English abstract)
[12] 廖玲,谢红薇,袁倩倩. 基于TSP问题的免疫算法研究[J]. 电脑开发与应用,2010,23(4):20-22.
Liao Ling, Xie Hongwei, Yuan Qianqian. Research on immune algonrithm based on TSP problem[J]. Computer Development & Applications, 2010, 23(4): 20-22. (in Chinese with English abstract)
[13] 刘克胜,曹先彬,郑浩然,等. 基于免疫算法的TSP问题求解[J]. 计算机工程,2000,26(1):1-2.
Liu Kesheng, Cao Xianbin, Zheng Haoran, et al. Solving TSP based on immune algorithm[J]. Computer Engineering, 2000, 26(1): 1-2. (in Chinese with English abstract)
[14] 田素博,王荣华,邱立春. 温室穴盘苗自动移栽输送系统设计[J]. 沈阳农业大学学报,2009,40(5):620-622.
Tian Subo, Wang Ronghua, Qiu Lichun. Design on conveyor system of automatic transplanting for plug seedling in greenhouse[J]. Journal of Shenyang Agricultural University, 2009, 40(5): 620-622. (in Chinese with English abstract)
[15] Tong Junhua, Jiang Huanyu, Zhou Wei. Development of automatic system for the seedling transplanter based on machine vision technology[J]. Proceedings of the 2012 IEEE International Conference on Computer Science and Automation Engineering (CSAE), 2012: 742-746.
[16] 蒋焕煜,施经挥,任烨,等. 机器视觉在幼苗自动移钵作业中的应用[J]. 农业工程学报,2009,25(5):127-131.
Jiang Huanyu, Shi Jinghui, Ren Ye, et al. Application of machine vision on automatic seedling transplanting[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(5): 127-131. (in Chinese with English abstract)
[17] 田素博,邱立春,张诗. 基于PLC的穴盘苗移栽机械手控制系统设计[J]. 沈阳农业大学学报,2007,38(1):122-124.
Tian Subo, Qiu Lichun, Zhang Shi. Control system of transplanting potted seedlings manipulator based on PLC[J]. Journal of Shenyang Agricultural University, 2007, 38(1): 122-124. (in Chinese with English abstract)
[18] 孙国祥,汪小旵,何国敏,等. 穴盘苗移栽机末端执行器设计与虚拟样机分析[J]. 农业机械学报,2010,41(10):48-53.
Sun Guoxiang, Wang Xiaochan, He Guomin, et al. Design of the end-effector for plug seedlings transplanter and analysis on virtual prototype[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(10): 48-53. (in Chinese with English abstract)
[19] 李月. 基于遗传算法的免疫算法对TSP问题的改进与研究[J]. 中国传媒大学学报:自然科学版,2017,24(4):58-63.
Li Yue. Improvement and research on TSP problem by immune algorithm based on genetic algorithm[J]. Journal of Communication University of China: Science and Technology, 2017, 24(4): 58-63. (in Chinese with English abstract)
[20] 王磊,潘进,焦李成. 免疫算法[J]. 电子学报,2000,28(7):74-78.
Wang Lei, Pan Jin, Jiao Licheng. The immune algorithm[J]. Acta Electronica Sinica, 2000, 28(7): 74-78. (in Chinese with English abstract)
[21] De Castro L N, Von Zuben F J, Learning and optimization using the clonal selection principle[J]. Ieee Transactions on Evolutionary Computation, 2002, 6(2): 239-251.
[22] 高辉,徐光辉,王哲人,等. 克隆选择算法在一类有竞争的物流配送中心选址问题中的应用[J]. 公路交通科技,2007,24(6):144-147.
Gao Hui, Xu Guanghui, Wang Zheren, et al. Application of clonal selection algorithm on competitive location model of logistics distribution center[J]. Journal of Highway and Transportation Research and Development, 2007, 24(6): 144-147. (in Chinese with English abstract)
[23] Wang Lei, Pan Jin, Jiao Li-Cheng. The immune programming[J]. Chinese Journal of Computers, 2000, 23(8): 806-812.
[24] 王磊. 免疫进化计算理论及应用[D]. 西安:西安电子科技大学,2001.
Wang Lei. Immune Evolutionary Computation and its Application[D]. Xi’an: Xi Dian University, 2001. (in Chinese with English abstract)
[25] 王琼,吕微,任伟建. 免疫遗传算法及在优化问题中的应用综述[J]. 计算机应用研究,2009,26(12):4428-4431.
Wang Qiong, Lv Wei, Ren Weijian. Immune genetic algorithm and applications in optimization[J]. Application Research of Computers, 2009, 26(12): 4428-4431. (in Chinese with English abstract)
[26] 莫宏伟,金鸿章. 免疫算法原理与应用[J]. 航空计算技术,2002,32(4):49-51.
Mo Hongwei, Jin Hongzhang. The principle and application of immune algorithm[J]. Aeronautical Computer Technique, 2002, 32(4): 49-51. (in Chinese with English abstract)
[27] 郁磊. MATLAB智能算法30个案例分析[M]. 北京:北京航空航天大学出版社,2015.
[28] 李菁,王宗军,邹彤. 求解车辆路径问题的免疫算法[J]. 数学的实践与认识,2005,35(7):178-183.
Li Jing, Wang Zongjun, Zou Tong. Immune algorithm for vehicle routing problem[J]. Mathematics in Pracrice and Theory, 2005, 35(7): 178-183. (in Chinese with English abstract)
[29] Forrest Stephanie, Javornik Brenda, Smith Robert E, et al. Using genetic algorithms to explore pattern recognition in the immune system[J]. Evolutionary Computation, 1993, 1(3): 191-211.
[30] 郑日荣,毛宗源,罗欣贤. 基于欧氏距离和精英交叉的免疫算法研究[J]. 控制与决策,2005,20(2):161-164,169.
Zheng Rirong, Mao Zongyuan, Luo Xinxian. Artificial immune algorithm based on euclidean distance and king-crossover[J]. Control and Decision, 2005, 20(2): 161-164, 169. (in Chinese with English abstract)
Optimization of automatic transplanting path for plug seedlings in greenhouse
Zhang Lina, Tan Yu, Lyu Haotun※, Li Baosheng, Jiang Yiyu, Wang Shuo
(,,100083,)
In mechanized plug seedling production, it is necessary to eliminate inferior plug seedlings and replant healthy plug seedlings with transplanter. In order to improve the plug seedling transplanting efficiency, plug seedling transplanting path would be planned. In this paper, the Clone Selection Algorithm(CSA) model and Immune Genetic Algorithm(IGA) model were constructed to solve the problem of transplanting path optimization of plug seedlings in greenhouse. Compared with the common sequence method and the Genetic Algorithm(GA), the simulation and verification tests of the transplanting path planning were carried out with 50-hole, 72-hole, and 128-hole plug trays. Set the population size in the CSA model to 40, the mutation probability to 0.4, and the number of clones to 10. Set the total population size in the IGA model to 40 (of which the memory cell bank capacity was 10), and the crossover probability to 0.5, the mutation probability was 0.4, and the diversity evaluation parameter was 0.95. The results showed that CSA and IGA model designed in this paper could achieve the purpose of optimizing the plug seedling transplanting path. The planned path length of the two models was similar, and the planned path length of two models was significantly shortened compared with the common sequence method and the GA. In the verification tests, the planned path length of common sequence method, GA model, CSA model and IGA model were 52 998, 50 807, 48 977 and 48 945 mm respectively. Compared with the common sequence method and the GA, the planned path length of CSA model and IGA model were shortened by 7.59% and 7.65%, and shortened by 3.60% and 3.66% compared with the GA model. The path planning efficiency of IGA model was higher than that of the CSA model, the calculation time of GA model, CSA model and IGA model was 3.23, 5.86 and 2.72 s respectively, the calculation time of IGA model was 15.79% less than that of the GA model. The models designed in this paper were suitable for path optimization of various-size plug seedlings automatic transplanting in greenhouse, it only needed to get the coordinates of plug seedlings according to the actual needs.
greenhouse; plug seedling; optimization; automatic transplanting; path planning; Clone Selection Algorithm; Immune Genetic Algorithm
张丽娜,谭彧,吕昊暾,等.温室穴盘苗自动移钵路径优化[J]. 农业工程学报,2020,36(15):65-72.doi:10.11975/j.issn.1002-6819.2020.15.008 http://www.tcsae.org
Zhang Lina, Tan Yu, Lyu Haotun, et al. Optimization of automatic transplanting path for plug seedlings in greenhouse [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(15): 65-72. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2020.15.008 http://www.tcsae.org
2020-03-11
2020-07-22
国家重点研发计划(2016YFD0700302)
张丽娜,博士生,主要从事机电一体化研究。Email:2271426674@qq.com
吕昊暾,博士,讲师,主要从事机电一体化研究。Email:lvhaotun@cau.edu.cn
10.11975/j.issn.1002-6819.2020.15.008
S24
A
1002-6819(2020)-15-0065-08
