基于蚁群算法的植保无人机任务分配优化研究

杜芳芳，巨玉祥，李 卓，王苗苗，常娜娜

(1.兰州资源环境职业技术学院，甘肃 兰州 730000；2.兰州交通大学，甘肃 兰州 730070)

随着我国农业生产模式由传统的手工作业向高科技精准农业转变，作业模式呈现出农业智能化、机械化等特征，而无人机以其机动灵活、生产作业效率高、综合应用成本低等特性在高科技精准农业中得到了广泛的应用[1-2]。尤其在农作物精准播种、实时监测、灾害治理、农药喷洒、产量预估等各个方面更是大显身手[3]。应用植保无人机喷洒农药不仅提升工作效率，减少浪费，还极大地避免了农药对人体的伤害[4]。无人机的农药喷洒作业过程，是采用无人机在规定的农田区域范围内进行覆盖式喷洒，并在最短的时间内实现效益最大化[5]。图1为经典的无人机区域全覆盖式农药喷洒方式示意图，其中：r为无人机农药喷洒航线半距，d为航线平距。此种方式大大增加了无人机的作业效率，减少了无人机作业航线的交叉[6]。

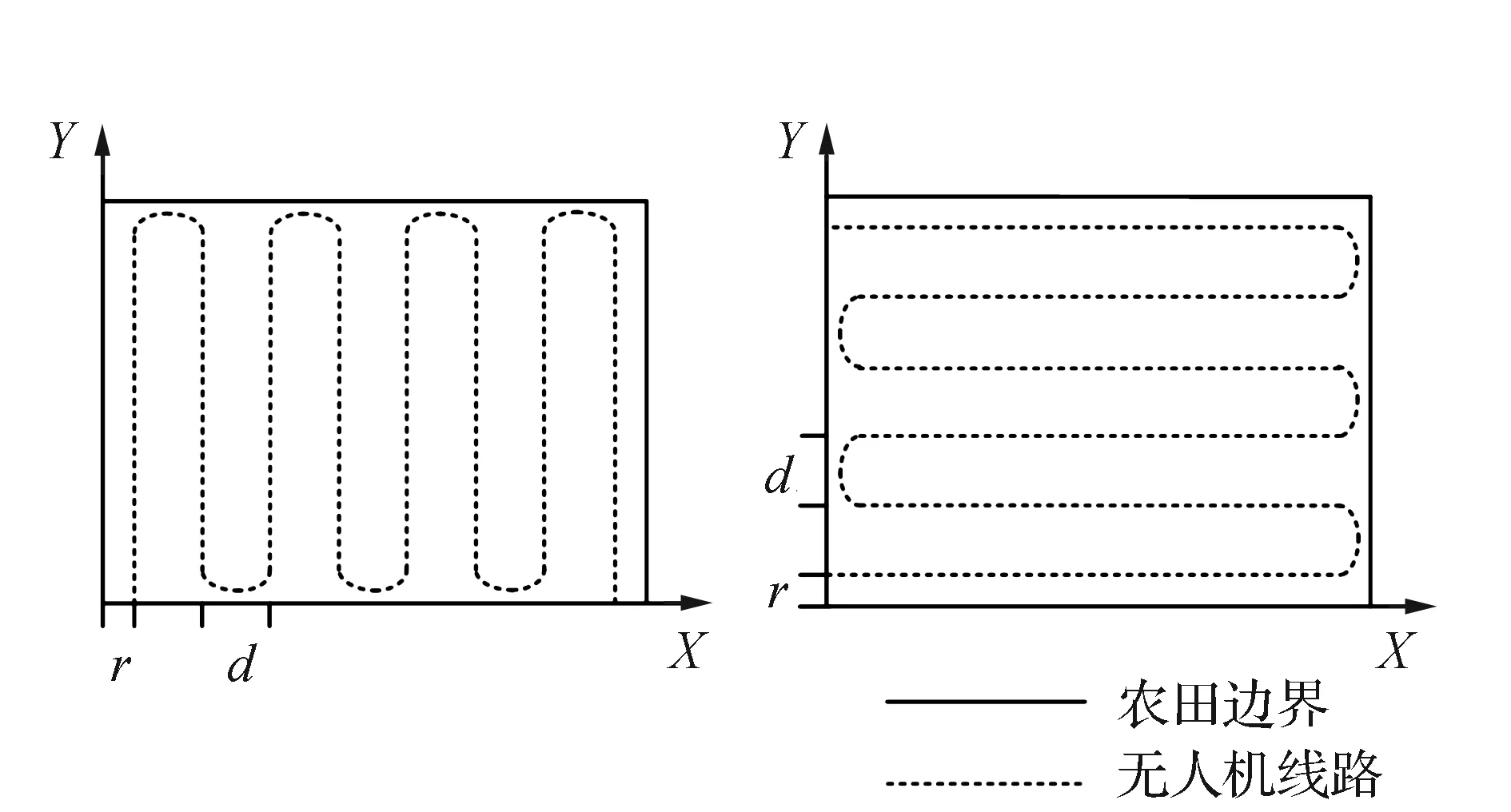
图1 无人机覆盖式喷洒农药图

无人机航线规划就是通过设计一种最优航线，进而使无人机避免遭遇障碍、威胁的问题[7]。无人机在军事战争应用方面，通过航线规划，有效躲避障碍威胁，提高军用无人机的生存及作战能力[8]。李柠[9]等提出基于改进的遗传算法，有效解决了多无人机协同航线规划问题。田伟[10]将遗传算法与Dijkstra算法结合到蚁群算法中，使无人机以最小的发现概率和可接受的飞行距离到达目的地，提高了无人机的应用能力。现如今，无人机也逐渐应用于精准农业领域，但无人机航线规划在农业领域的研究却相对较少；徐博[11]等以植保无人机农药喷洒过程中作业架次最少为约束，工作能耗最小为目标，将工作区域利用栅格法进行划分，基于一种多架次返航路线规划算法，合理规划植保无人机农药喷洒路线，通过给出的算法规划一块210 m×200 m的矩形农田农药喷洒无人机航线，工作能耗节省明显，且作业区域越大，优势越明显；徐正伟[12]基于改进的遗传算法，以作业时间最小为目标，构建多植保无人机任务分配模型；彭孝东，张铁民[13]等以水稻田边界为参照对象，基于GPS坐标定位，进行植保无人机喷雾航线规划飞行试验，试验结果表明，理想情况下无人机作业遗漏率、重复率较大，区域外浪费较为严重，并提出以GPS导航为主，在规定区域内进行无人机航线规划是精准农业发展的主流方向。

既有研究表明，植保无人机农药喷洒航线规划具有非常重要的意义，但目前研究只针对某个固定区域内部无人机航线进行规划，以期得到最优飞行航线。而实际当中，农作物种植并不都以一大整块农田为主，有些作物以小面积分散种植。基于此，结合既有研究，考虑多块农田之间喷洒次序不同所造成的资源浪费问题，借鉴科学成熟的无人机任务分配方式及航线规划方法，并结合具体情况，规划无人机农药喷洒过程中的作业任务分配有着十分重要的意义。

1 无人机任务分配模型

1.1 问题描述

我国幅员辽阔，地形复杂，很多地区的农作物种植以小面积分散种植为主。基于此，在多个小面积农作物种植区域，植保无人机农药喷洒线路规划不仅包含每个农田内部的线路走向，还包含每个作业区域之间的作业次序规划。具体而言，即可归结为TSP问题，本文仅考虑每个作业区域之间的次序选择，对于区域内部的具体线路规划不予考虑，使得植保无人机在满足每个区域需求的同时，总飞行里程最短。

要解决的问题及基本假设：

1)无人机从物资补给中心出发，完成任务后返回补给中心；

2)每片农田仅由一架无人机访问且只能被访问一次，其农药需求量不能超过飞机载重量；

3)无人机为相同机型且携带农药总量不能超出中心农药拥有量；

4)每片农田的坐标、农药喷洒量和喷洒持续时间已知。

1.2 模型构建

1.2.1 模型参数

表1 模型参数及变量

1.2.2 模型构建

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Tik+sti+tijk≤Tjk+C(1-xijk),

∀i,j∈V0,k∈K,

(9)

xijk∈{0,1}∀i,j∈V,k∈K,

(10)

Qk,qi,sti>0i∈V0,k∈K.

(11)

式(1)表示最小化里程的目标函数；式(2)、式(3)表示每片农田仅被1架无人机服务且仅访问1次；式(4)为子回路消去约束；式(5)表示无人机从中心出发最终返回补给中心；式(6)为节点平衡约束；式(7)为无人机载重约束；式(8)为无人机续航时间约束；式(9)表示无人机从结束上片农田到访问下一片农田所要满足的时间条件；式(10)、式(11)为决策变量和参数约束。

2 求解模型的蚁群算法

因任务分配问题的求解规模较大，精确算法无法在可接受的计算时间内得到最优解。传统启发式算法求解大规模问题已得到广泛应用，如遗传算法、禁忌搜索算法和模拟退火算法等均表现出良好的求解效果。因此，本文将蚁群算法应用于模型的求解，用染色体代表一个可行解，通过交叉、变异等操作对种群进行更新，经过若干次迭代在可接受的时间内得到一个满意解。

2.1 算法原理

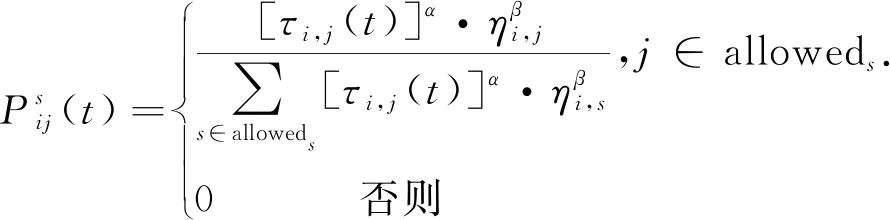
(12)

式中:α为信息素重要度因子；β为启发式信息重要度因子；alloweds=V/{tabus}为蚂蚁s下一步允许访问的节点集合;tabus为蚂蚁s访问过的节点集合，即路径禁忌表。

启发式函数ηij(t)越大，蚂蚁选择节点j的概率越大。随着迭代次数的增加，路径(i,j)的信息素浓度τij不断叠加，同时残留的信息素将持续挥发，则(t+1)时刻路径(i,j)的信息素τij(t+1)浓度更新规则为：

(13)

(14)

式中:ρ为信息素挥发系数；Q为全局信息素常量；固本文模型目标是成本最小，则cost(i,j)为路径(i,j)上的成本。

2.2 交叉、变异

通过交叉完成配送序列的更新。分别对个体pi和个体pj随机选择一个交叉序列、交换序列内的染色体，形成新的个体，如图2。

图2 交叉操作

通过变异操作搜索配送序列的邻域。对个体pk选择两个插入点，交换插入点的元素个体。如图3。

图3 变异操作

3 算例分析

3.1 仿真试验设置

算例的试验数据通过Matlab软件随机生成1个植保无人机物资给予调度中心和19个大小不同的农田(面积在0.53～0.8 hm2之间)，由于本文对于农田内部的植保无人机具体航线不予详细考虑，因此对于每个农田以其几何中心为目标点进行简化，所有点随机分布在(0,70 km2)的平面坐标内，其具体信息见表2。植保无人机的具体参数配置情况见表3。

表2 植保无人机作业区域信息表

表3 无人机基本参数配置表

3.2 模型计算结果及分析

基于本文构建的以最小化植保无人机作业里程最短为目标，通过Matlab软件编写程序，对模型进行100次循环迭代。

所有算法运行迭代在一台搭载2.4 GHz的Intel(R) Core(TM) i5处理器和8 GB内存的计算机平台上实现，作业路径优化结果和算法收敛曲线见图4、图5所示。

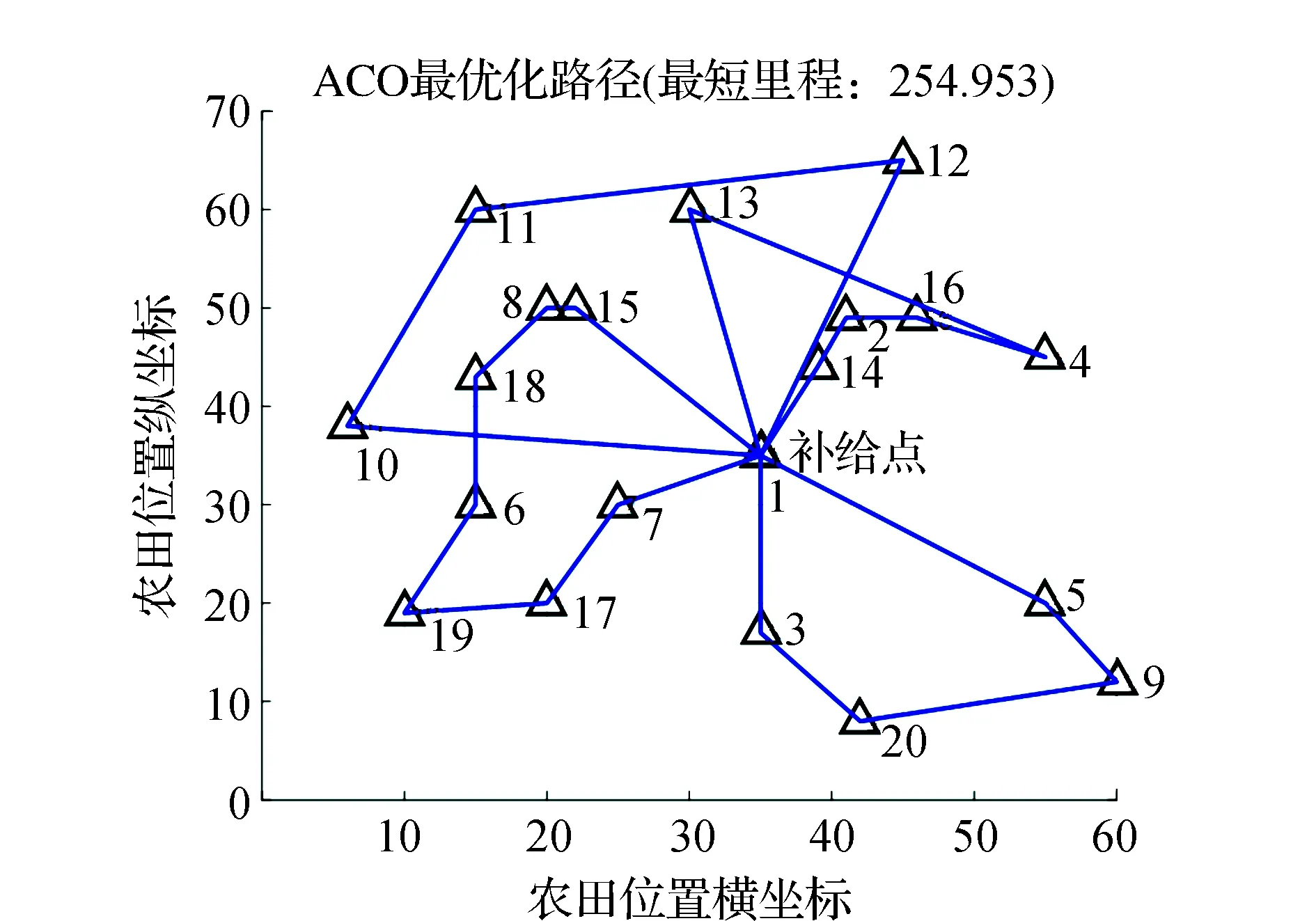
图4 最优飞行路径示意

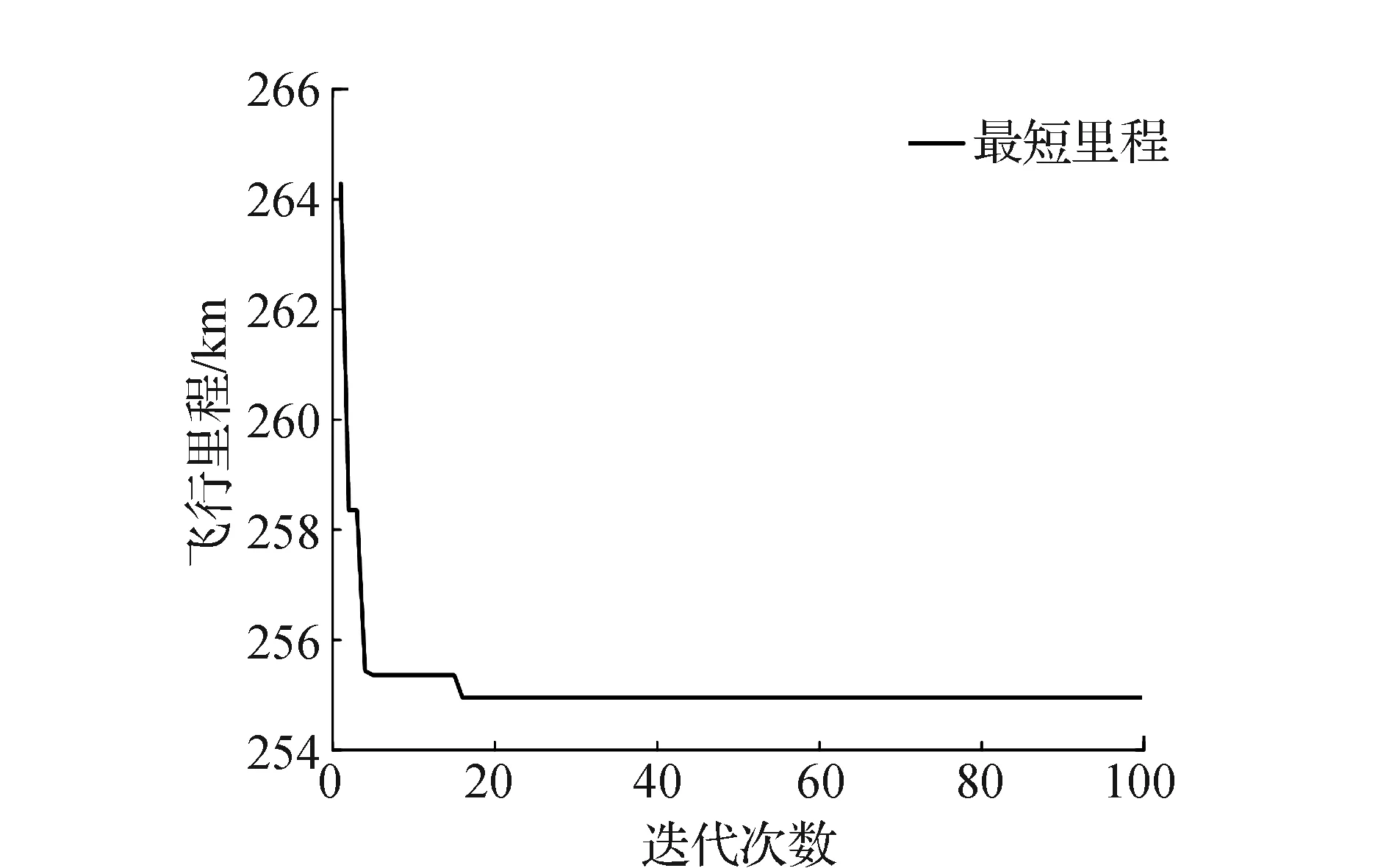
图5 算法收敛曲线

如图4所示，本文模型和算法可以在可接受的计算时间内有效求解无人机喷洒农药的任务调度工作。考虑到无人机连续飞行时间的限制和无人机的载重限制，即续航时间和所携带的农药质量，在路径求解中需要兼顾时间约束和载重约束，因此，在飞行工作一定时间或所携带药量不足以满足下一农田喷洒任务时，无人机需要返回物资补给点，补给后再次起飞喷洒剩余农田。依据本文模型及算法设定参数，求得最短飞行里程为254.953 km，最短作业里程路径为1-14-2-16-4-13-1-7-17-19-6-18-8-15-1-3-20-9-5-1-12-11-10-1。

如图5所示，对模型进行100代循环求解，可以看出算法收敛速度较快，下降趋势明显，在前20代求得近似最优解，能够有效解决本文路径规划问题。

4 结 论

本文提出一种以飞行里程最短为目标的无人机农药喷洒作业路径调度模型，考虑了无人机续航时间的限制和飞行器载重量的限制，通过蚁群优化算法求解模型。所求的路径中包含多个子任务路径，能够为农业部门的智慧农业提供重要参考。

本文从宏观上优化了无人机的飞行路径，而从更微观角度考虑农田内飞行轨迹的整体路径优化将是下一步研究的重点。