基于近似理论水驱曲线的油藏水驱体积波及系数动态计算方法
2020-09-18张金庆李文忠周文胜冯其红
刘 晨,张金庆,李文忠,周文胜,冯其红
(1.中国石油大学(华东)石油工程学院,山东青岛 266580;2.海洋石油高效开发国家重点实验室,北京 100028;3.中海油研究总院有限责任公司,北京 100028;4.中海石油(中国)有限公司天津分公司,天津 300459)
水驱体积波及系数是油藏开发过程中的重要参数,准确把握水驱体积波及系数的变化规律有助于油田开发技术政策的合理制定[1-2]。目前水驱体积波及系数的研究主要包括室内实验、油藏数值模拟以及水驱特征曲线等方法[3-8]。室内实验法和油藏数值模拟法均以岩心实验数据为基础,难以准确反映整个油藏真实情况。水驱特征曲线法基于油藏实际的生产数据,可较客观全面地评价油藏的整体水驱体积波及规律,受到了诸多学者的关注。目前水驱特征曲线法计算水驱体积波及系数可分为3种方法:①假设水驱油过程中驱油效率始终为恒定值[9-12],忽略波及区内驱替程度的变化,由此将导致不同含水率阶段计算的水驱体积波及系数小于实际值。②胡罡提出的方法,考虑了水驱过程中驱油效率的变化,但在推导过程中驱油效率采用出口端含水饱和度计算,不符合常规认识,且方法未能得到有效验证[13-14]。③有学者提出将岩心相对渗透率曲线与水驱曲线相结合的计算方法[15-17],该方法克服了上述2 种方法存在的问题,可较客观地计算中高含水率及特高含水率阶段的水驱体积波及系数,但计算精度受控于岩心相对渗透率资料的可靠性和代表性,仅适用于储层均质性较好、油水渗流规律较统一、相对渗透率具有代表性的油藏,难以满足沉积类型多样、非均质性强等储层内部油水渗流规律多样的复杂油藏。
为此,笔者基于近似理论水驱曲线和Welge 方程线性表达式建立了新型的水驱体积波及系数和驱油效率动态计算方法。新方法仅需要累积产油量和累积产水量等实际生产动态数据,不需要拟合岩心相对渗透率曲线,可满足复杂油藏的计算需求。同时,由于近似理论水驱曲线可实现不同类型油藏在各含水率阶段的动态精细刻画[18-22],因此,新方法不仅能适用各种类型油藏,同时还可实现水驱前缘突破后各开发阶段的准确计算,在油田动态分析和开发效果评价等方面具有广泛的应用前景。
1 新方法的建立
1.1 含水饱和度与含水率定量表征关系
油、水相相对渗透率曲线通常采用幂函数表示[23-24],其表达式为:

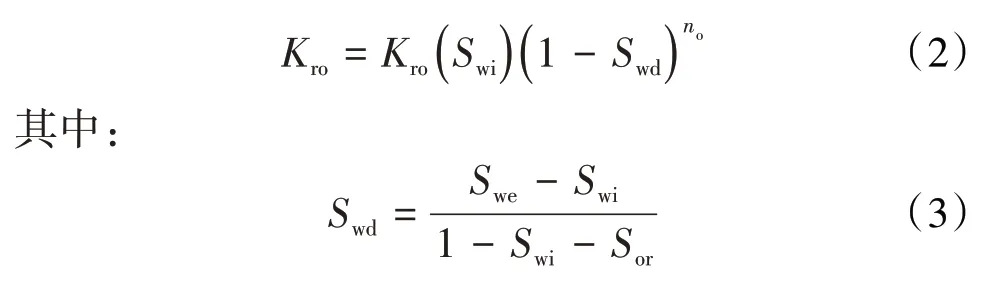
忽略毛细管力和重力作用,分流量方程表示为:
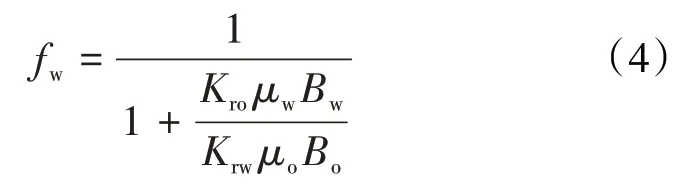
将(1)式和(2)式代入(4)式可得:

(5)式为fw与Swd的函数关系式,其反函数可近似表示为[25]:
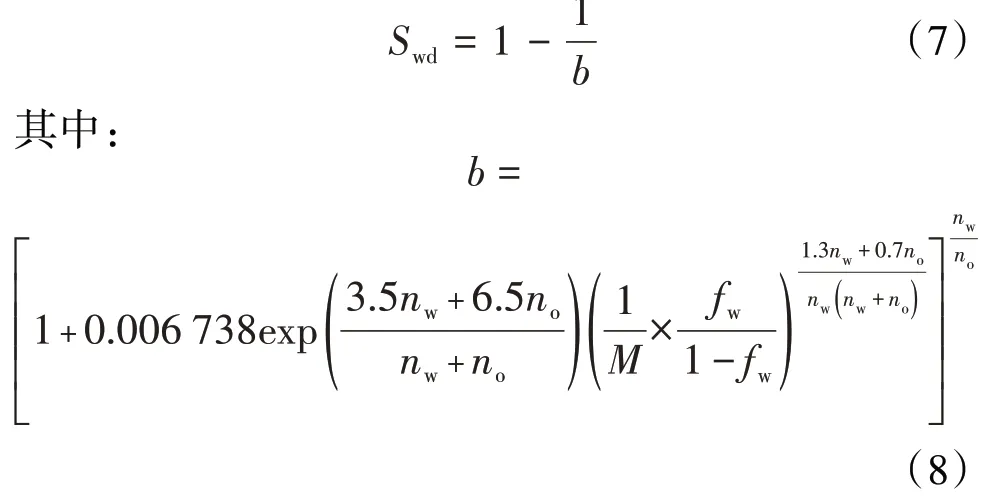
可通过(7)式计算不同含水率对应的含水饱和度。
1.2 驱油效率与含水率定量表征关系
油、水两相区含水饱和度与出口端含水饱和度的关系可由Welge方程表示[26]:

对(5)式求导,并代入(9)式可得:
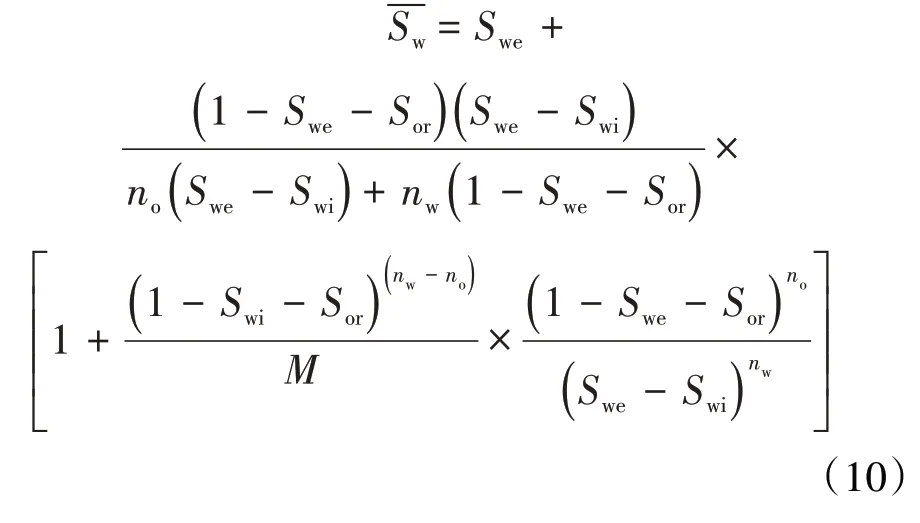
文献[27]提出了Welge 系数的概念,并将(10)式简化为线性表达式:

水驱油藏驱油效率计算公式为:

采用(11)式Welge 方程的线性表达式,并结合(7)式和(12)式可得水驱驱油效率与含水率变化关系为:

1.3 体积波及系数与含水率定量表征关系
将(5)式积分可得新型的近似理论水驱曲线[28-29]的方程式为:
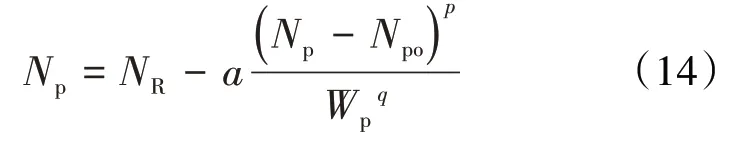
将(14)式对时间求导,可得含水率与累积产油量关系式为:

由(15)式通过迭代计算可以得到不同含水率对应的累积产油量。在此基础上即可求得不同含水率时的水驱采出程度表达式为:

同时,水驱采出程度还可表示为:

将(13)式代入(17)式,可得到水驱体积波及系数计算公式为:

1.4 关键参数计算
(18)式中的w,nw,no和M等4 个参数,其中nw,no和M与近似理论水驱曲线特征参数的关系[28-29]为:


Welge方程中的系数w可由下式迭代求解[29]:
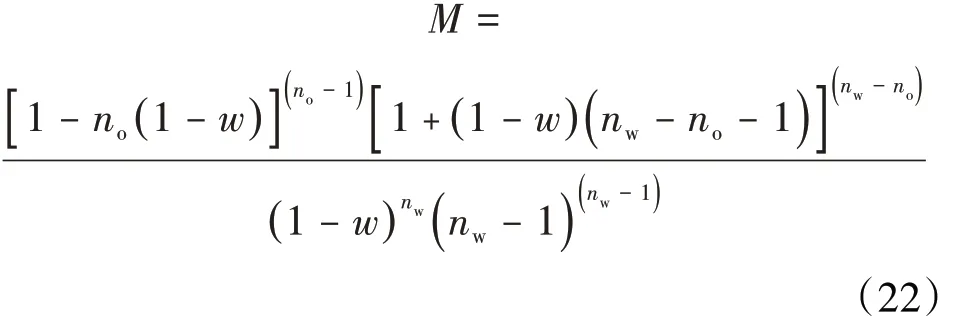
新方法计算步骤主要包括:①根据累积产油量和累积产水量等实际生产动态数据进行近似理论水驱曲线拟合,求取特征参数p,q,a和可动油储量NR。②根据(19)式—(21)式可计算油、水相指数和水油流度比。③根据(22)式计算Welge 方程中的系数w。④根据(13)式和(18)式计算不同含水率时的水驱体积波及系数和驱油效率。
2 新方法验证
为了验证新方法的可靠性,选取文献[15-16]中的2 个开发实例进行对比分析,这2 个油藏均通过拟合典型的岩心相对渗透率曲线得到较为可靠的开发中后期的水驱体积波及系数变化规律。其中,渤海南部BZ 油田A 井区S1 砂体为常规中、高渗透率稀油储层,平均渗透率为700 mD,储层均质性较好、油水渗流规律简单,地层原油黏度为4.5 mPa·s,地层水黏度为0.5 mPa·s,实验岩心分析束缚水饱和度为0.289,残余油饱和度为0.214,经过10 a 开发,综合含水率为96.1%,采出程度为28.8%[15];鄯善油田三间房组油藏为低渗透率、低黏度砂岩储层,平均渗透率为6.2 mD,地层原油黏度为0.388 mPa·s,地层水黏度为0.343 mPa·s,实验岩心分析束缚水饱和度为0.375,残余油饱和度为0.321,经过28 a 开发,综合含水率为94.6%,采出程度为23.8%[16]。根据BZ 油田S1 砂体历年生产数据进行近似理论水驱曲线拟合,得到S1砂体的近似理论水驱曲线特征参数:p=2.1,q=0.8,a=0.384 4,NR=114.412 1,根据(19)式—(22)式计算得到nw=1.625,no=2.25,M=4.699 3,w=0.724 2。同理可得鄯善油田三间房组油藏的相关参数:p=2.3,q=1.1,a=0.047 8,NR=886.856 8,nw=1.090 9,no=1.909 1,M=0.452 7,w=0.482 3。根据(18)式还可得到2个开发实例油藏不同含水率时的水驱体积波及系数。
由近似理论水驱曲线预测的生产动态数据与实际对比(图1)可知,2个开发实例油藏近似理论水驱曲线预测的含水率和累积产水量,从油藏见水早期即与实际生产动态数据呈良好的吻合关系,表明近似理论水驱曲线具有适用范围广的优点,可准确表征不同含水率阶段的油藏生产动态。
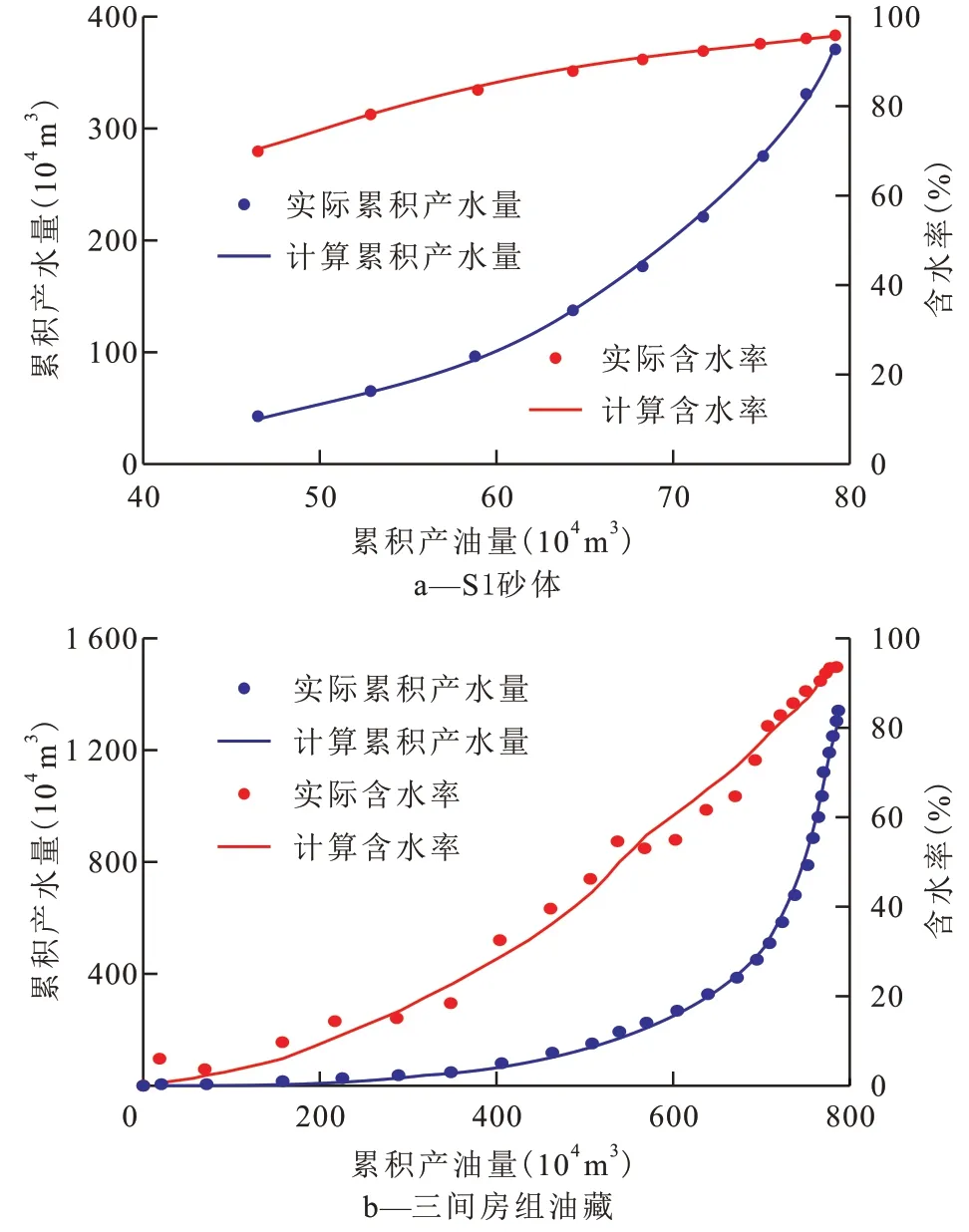
图1 2个开发实例油藏近似理论水驱曲线拟合效果Fig.1 Fitting effect of history production data of two case reservoirs based on the approximate theoretical water drive curve
由新方法与文献[15-16]计算的水驱体积波及系数对比(图2)可知,新方法计算结果与文献[15-16]基于岩心相对渗透率曲线的计算结果均呈一致的增长趋势,验证了新方法的可靠性。对于BZ油田S1 砂体,文献[15]计算的水驱体积波及系数随含水率变化规律与新方法的计算结果基本重合,在特高含水期稍有差异。新方法预测S1 砂体在含水率为96.0%时的水驱体积波及系数为52.3%,文献[15]中的预测值为48.8%,储层实际值为51.5%,新方法预测结果偏差1.6%,预测精度高于文献[15]的方法。对于鄯善油田三间房组油藏,文献[16]计算的水驱体积波及系数随含水率变化规律与新方法计算结果相比,在中高含水率阶段吻合程度较高,在中低含水率阶段存在一定差异,表现在含水率达到45%后吻合程度较好,因此文献[16]预测研究区在中低含水率阶段的水驱体积波及系数不能准确地反映油藏真实情况;而由图1可以看出,采用新方法时该油藏从含水率为18%即开始较好地拟合,故新方法预测的水驱体积波及系数更为可靠。由于新方法基于适用范围较广的近似理论水驱曲线,同时避免了油藏内部渗流差异带来的干扰,因此,新方法不仅能适用更广泛的油藏类型,同时还可实现水驱前缘突破后各含水率阶段的准确表征,预测精度提升。

图2 2个开发实例油藏水驱体积波及系数随含水率的变化关系Fig.2 Relationship between water drive volume sweep coefficient and water cut in two case reservoirs
3 实例应用
曹妃甸油田是受构造控制的潜山—披覆背斜块状油藏,发育古近系孔隙型砂砾岩和太古界裂缝型花岗岩2 套储层,储层上、下叠置构成复合储集体,互相连通,具有统一的油水系统,内部油水渗流规律较复杂。砂砾岩储层孔隙度为15.0%~25.0%,渗透率为100~1 000 mD。潜山基岩为双孔双渗储层,有效孔隙度分布不均,裂缝发育,储层特征较复杂。地层原油密度为0.671 g/cm3,地层原油黏度为0.6 mPa·s,地层水黏度为0.3 mPa·s,为轻质原油。经室内实验分析,束缚水饱和度为0.225,残余油饱和度为0.130。曹妃甸油田边底水能量充足,天然能量开发10 a(图3),截止2019 年综合含水率为96.5%,采出程度仅为9.12%。
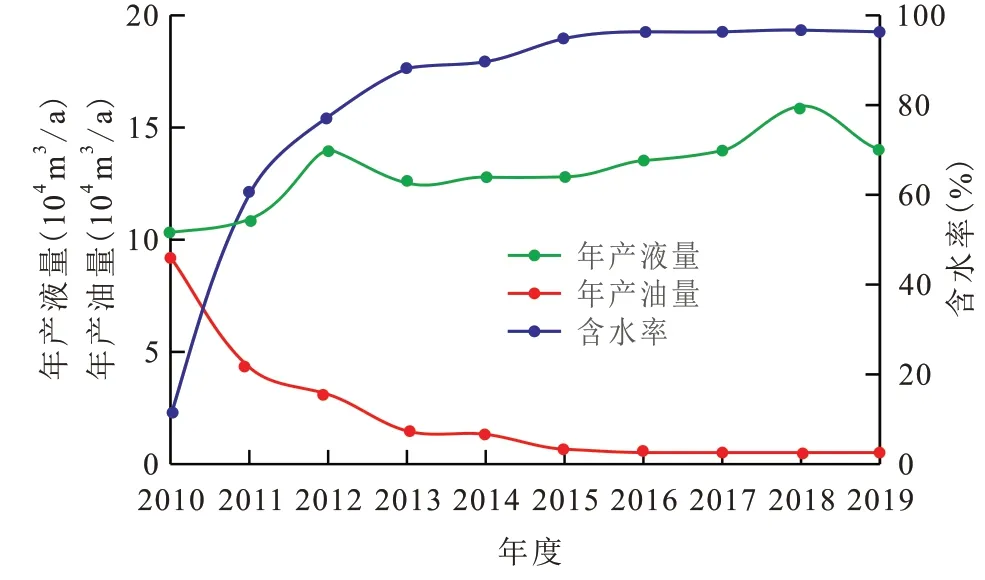
图3 曹妃甸油田实际生产动态数据Fig.3 Actual production dynamic data of Caofeidian Oilfield

图4 曹妃甸油田近似理论水驱曲线拟合效果Fig.4 Fitting effect of approximate theoretical water drive curve in Caofeidian Oilfield
根据曹妃甸油田10 a 实际生产动态数据构建(Np-Npo)p/Wpq与Np的线性关系(图4),拟合近似理论水驱曲线并求得相关参数:p=2.2,q=0.7,a=0.199 6,NR=28.58,nw=2.142 9,no=2.428 6,M=3.448 2,w=0.729 2。由图4 可知,曹妃甸油田近似理论水驱曲线拟合关系良好,不同含水率阶段预测的开发指标均与实际相吻合。研究表明,对于曹妃甸油田这种潜山裂缝与砂岩叠置的复合储层,应用近似理论水驱曲线仍然可以较准确地表征油田开发规律。
将曹妃甸油田近似理论水驱曲线特征参数代入(13)式即可得到水驱驱油效率随含水率变化关系(图5),再由(15)式可得到含水率与采出程度变化关系,从而根据(18)式得到水驱体积波及系数随含水率变化关系(图6)。

图5 曹妃甸油田水驱驱油效率随含水率变化关系Fig.5 Relationship between water drive displacement efficiency and water cut in Caofeidian Oilfield
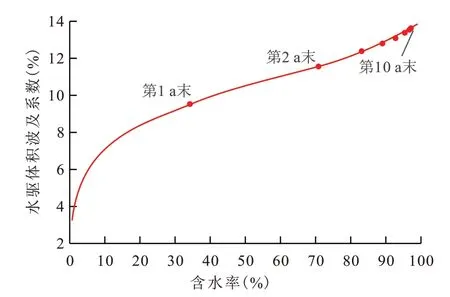
图6 曹妃甸油田水驱体积波及系数随含水率变化关系Fig.6 Relationship between water drive volume sweep coefficient and water cut in Caofeidian Oilfield
由图5 可知,曹妃甸油田水驱驱油效率随含水率变化呈近活塞式的驱替特征。开发初期驱油效率上升较快,投产第2 a 末驱油效率即达到49.32%,随后缓慢增长,开发后期受高强度水驱影响,驱油效率进一步提升。利用(13)式预测该油田综合含水率为98%时的水驱驱油效率达到69.79%,与室内实验认识一致。曹妃甸油田目前水驱驱油效率为66.01%,通过提高水驱驱油效率改善油田开发效果的潜力较小。
由图6 可知,曹妃甸油田水驱体积波及系数随含水率的增加逐渐增大,初期增速较快,其原因为曹妃甸油田断层、裂缝相对发育,开发初期边底水沿裂缝快速突进,水驱体积波及系数增长速度较快,投产4 个月后底水沿着裂缝突进到井筒附近,生产井出现水锥现象,含水率逐渐上升,投产当年年底瞬时含水率即达到34.14%,水驱体积波及系数达到9.54%,而后水驱体积波及系数进入缓慢增长阶段,继续生产9 a 后,水驱体积波及系数为13.63%,只增加了4.09%,预测油田综合含水率达到98%时水驱体积波及系数为13.81%,说明约86%的油田区域将无法有效波及。根据储层解释结果,曹妃甸油田裂缝孔隙度占总孔隙度的比重为12.65%,这表明曹妃甸油田在现有井网下仅有效动用了裂缝中的储量,而砂岩储层和潜山基质中的储量基本未动用。
4 结论
水驱体积波及系数目前是基于室内实验得到的油水相对渗透率曲线计算的。油水渗流规律多样的复杂油藏通常有多条油水相对渗透率曲线,目前计算方法难以适用。本文建立的水驱体积波及系数和驱油效率计算新方法从累积产油量和累积产水量等实际生产动态数据入手,通过实际生产动态数据即可准确得到油藏不同含水率阶段水驱体积波及系数和驱油效率的变化规律。由于不需要拟合油、水相相对渗透率曲线,新方法可适用于各种类型油藏,解决了复杂油藏水驱体积波及系数难以计算的难题。新方法计算简便、结果可靠,可广泛应用于油田动态分析、开发效果评价等工作。
符号解释
a,p,q,NR——近似理论水驱曲线特征参数;
Bo——地层原油体积系数;
Bw——地层水体积系数;
Ed——水驱驱油效率;
EV——水驱体积波及系数;
fw——含水率;
Kro——油相相对渗透率;
Kro(Swi)——束缚水饱和度下的油相相对渗透率;
Krw——水相相对渗透率;
Krw(Sor) ——残余油饱和度下的水相相对渗透率;
M——水油流度比;
no——油相指数;
nw——水相指数;
N——地质储量,104m3;
Np——累积产油量,104m3;
Npo——无水采油量,104m3;
R——水驱采出程度;
Sor——残余油饱和度;
Swd——归一化含水饱和度;
Swe——出口端含水饱和度;
Swi——束缚水饱和度;
w——Welge系数;
Wp——累积产水量,104m3;
μo——地层原油黏度,mPa·s;
μw——地层水黏度,mPa·s。
