模型试验中岩质相似材料配比研究

余沛侨,张书豪,张光泽，柴春阳

(西南交通大学地球科学与环境工程学院，四川成都 611756)

模型试验是目前研究复杂岩体的力学特征的一种重要研究手段，能解决比较复杂的地质条件下，岩土体的变形规律和受力情况。通过按照相似比进行缩尺，对于地质模型进行研究，可以反映地质原型的变形破坏规律。

而模型试验成功的关键在于模型相似材料的配比与制作，能否正确的反映地质原型的工程特性，目前对于岩体相似材料的研制，前人的成果丰硕。韩伯鲤等(1983)研制出了一红新型材料(MIB)，能较好地符合大多数相似材料的容重、弹性模量、强度的要求[1]。龚召熊等(1984)提出了凝胶剂以石蜡油、石膏、环氧树脂为主，在物理力学模型中得到了很好的应用[2]。马芳平等(2004)成功研制了NIOS地质力学材料，较好地应用在了地质力学模型中[3]。左保成等(2005)采用水泥、石膏、石英砂三种材料，配制出了的相似材料[4]。张强勇等(2008)提出了一种新型铁精砂相似材料(IBSCM)，以重晶石、石英砂、铁粉为骨料，石膏为调节剂，较好地适用于模型试验中[5]。目前的材料主要以骨料、胶结剂、调和剂进行分类，而骨料以重晶石粉、石英砂为主，胶结剂以石膏、水泥为主，调和剂主要是水、甘油等。所以，相似材料配制最为重要的五种材料为：石英砂、重晶石粉、水泥、石膏、水。

1 相似材料配比方案研究

本次配比试验采用重晶石粉、石英砂、石膏、水泥、水，以重晶石粉、石英砂为骨料，以石膏、水泥为胶结剂，水为调和剂进行配制。综合前任文献以及经验，采用了三个因素五水平的正交试验法。三个因素分别为：A胶结剂占材料的总重的比例、B水泥占胶结剂总重的比例、C重晶石粉占骨料总重的比例。为研究目标配比的影响范围，且为找到最关键影响因素，综合前人经验，所以将A因素的水平严格控制在一定范围，B因素和C因素则分布较广，A因素(胶结剂占材料的总重)范围:10 %～20 %，B因素(水泥占胶结剂总重)范围:30 %～70 %，C因素(重晶石粉占骨料总重)范围：20 %～60 %，然后范围内均分为5组水平，各水平见表1。具体采用L25(35)正交试验表(表2)。

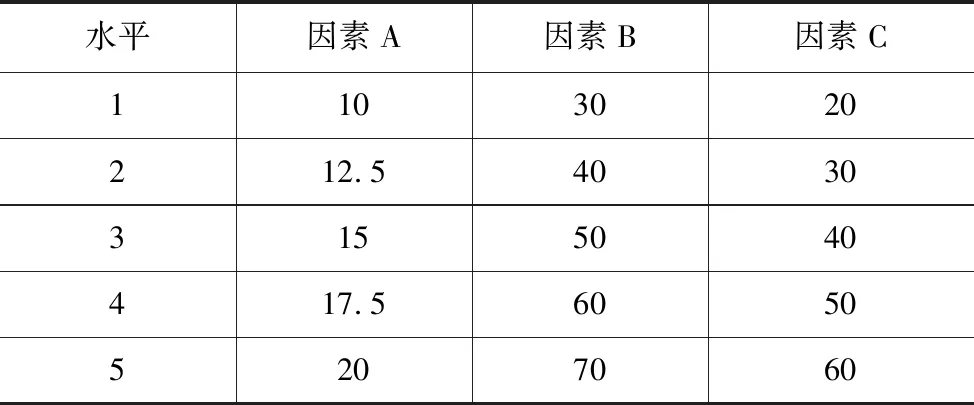
表1 各因素各水平 %

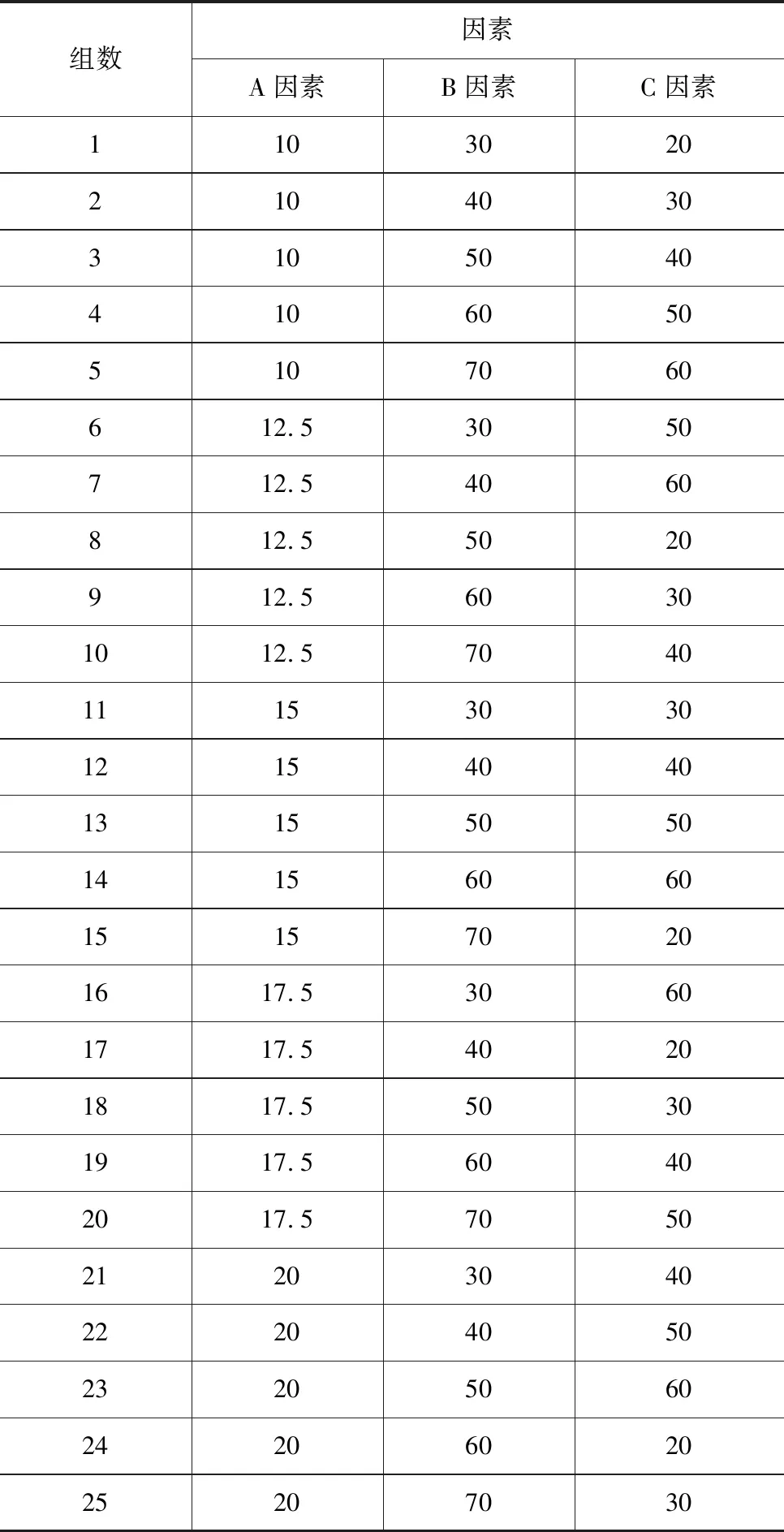
表2 相似材料配比试验方案 %

2 试验过程及结果

制作25组岩石试样，包括φ50 mm×φ50 mm和φ50 mm×φ100 mm圆柱体试样(图1)，分别进行单轴压缩实验、劈裂实验(图2)，得到密度、单轴抗压强度、抗拉强度、弹性模量四种物理力学参数，结果见表3。

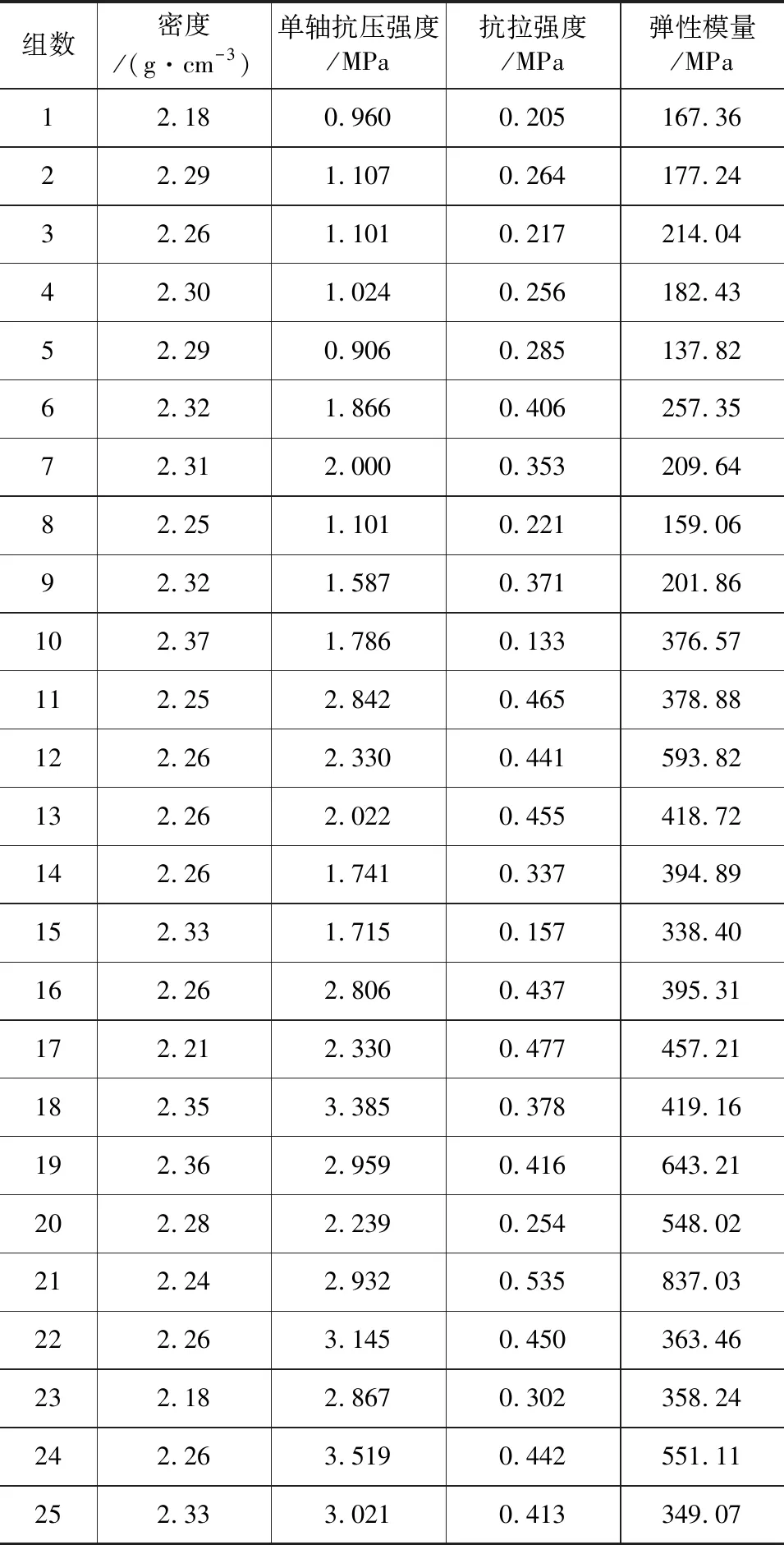
表3 试样的物理力学参数

图1 制作的部分试样

图2 单轴压缩实验与劈裂实验

3 实验结果分析

3.1 密度影响因素分析

3.1.1 极差分析

极差分析是正交试验最常用的分析方法，通过各水平均值的最大值与最小值之间的比较，反映该因子对指标的影响程度(詹志发等，2019)。通过密度的极差分析(表4)，可以直观得出各因素的影响程度：B>C>A。

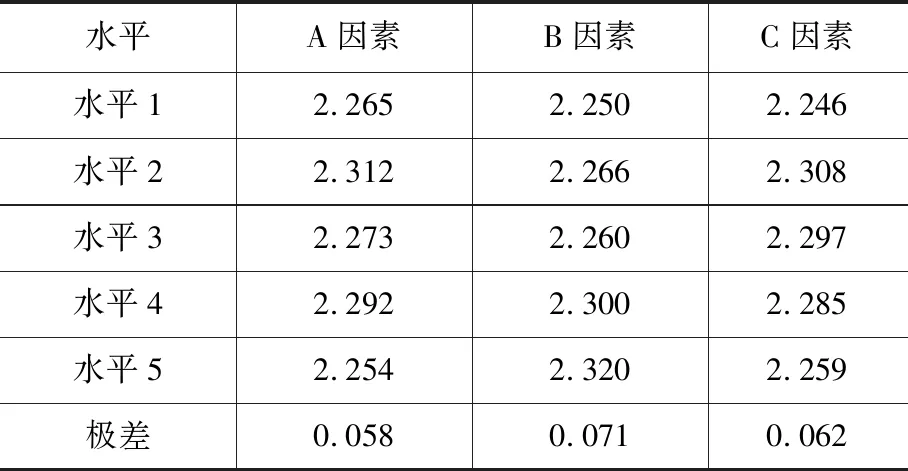
表4 密度的极差分析 g/cm3

3.1.2 方差分析

通过方差分析可以很好判断各因素的显著性影响(詹志发等，2019)。在置信水平α为0.1时，显著性水平F(4,8)=2.81。由表4知，各因素的显著性为：B>A>C，但对于密度均不显著，结合极差分析，可得B因素较为显著(表5、图3)。

表5 密度的方差分析

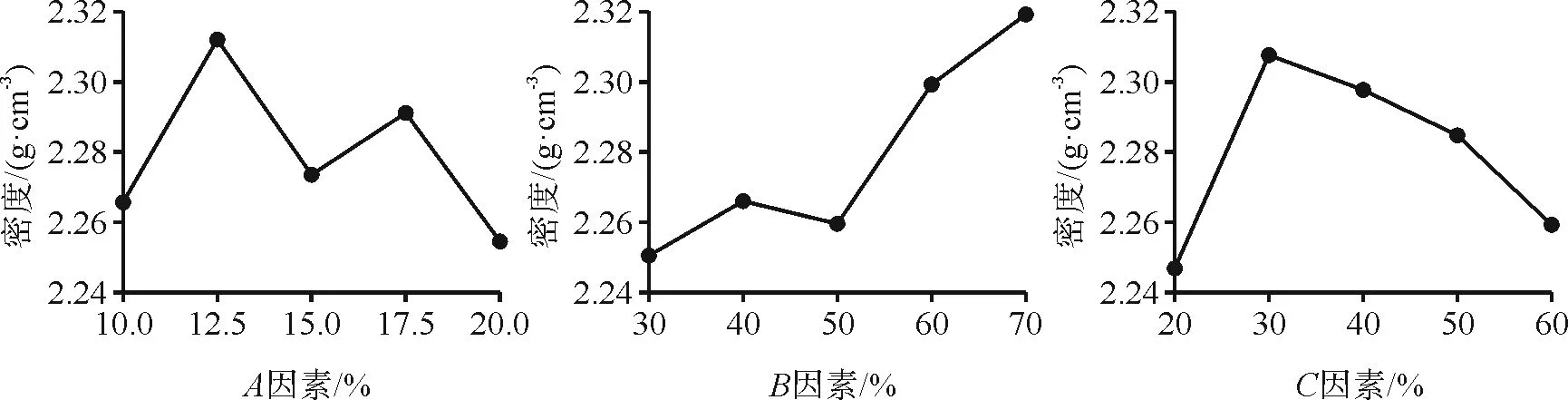
图3 密度的敏感性分析

3.2 抗压强度的敏感性分析

3.2.1 极差分析

将单轴抗压强度的各因素水平的均值通过统计，并且得出各因素的极差，见表4。通过密度的极差分析，可以直观得出各因素的影响程度：A>C>B。随着胶结剂占总量的比例(A因素)的增加，单轴抗压强度逐渐增大(表6)。

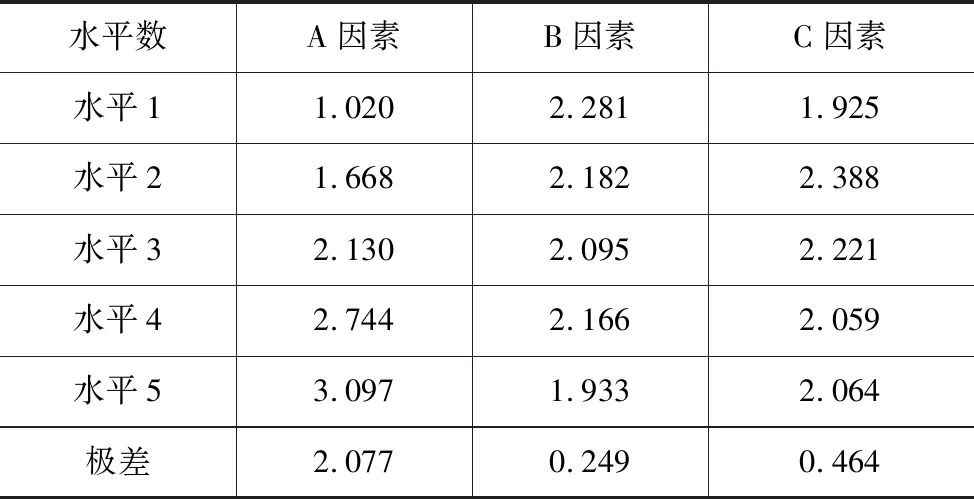
表6 抗压强度的极差分析 MPa

3.2.2 方差分析

在置信水平α为0.1时，显著性水平F(4,8)=2.81，由表5可知，各因素的显著性比较：A>C>B，A因素对单轴抗压强度非常显著，B因素与C因素对抗压强度不显著，结果与极差分析一致(表7、图4)。

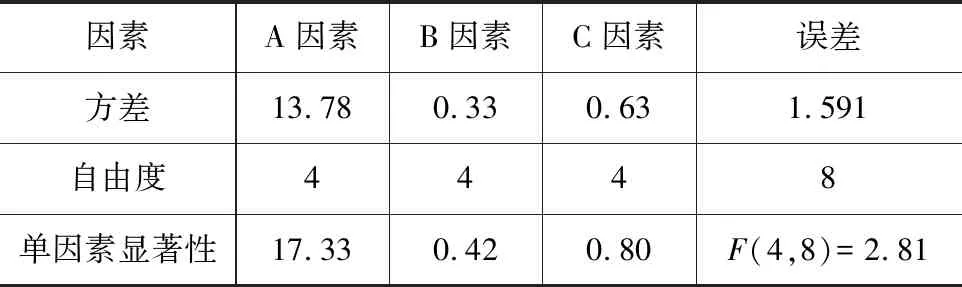
表7 抗压强度的方差分析表

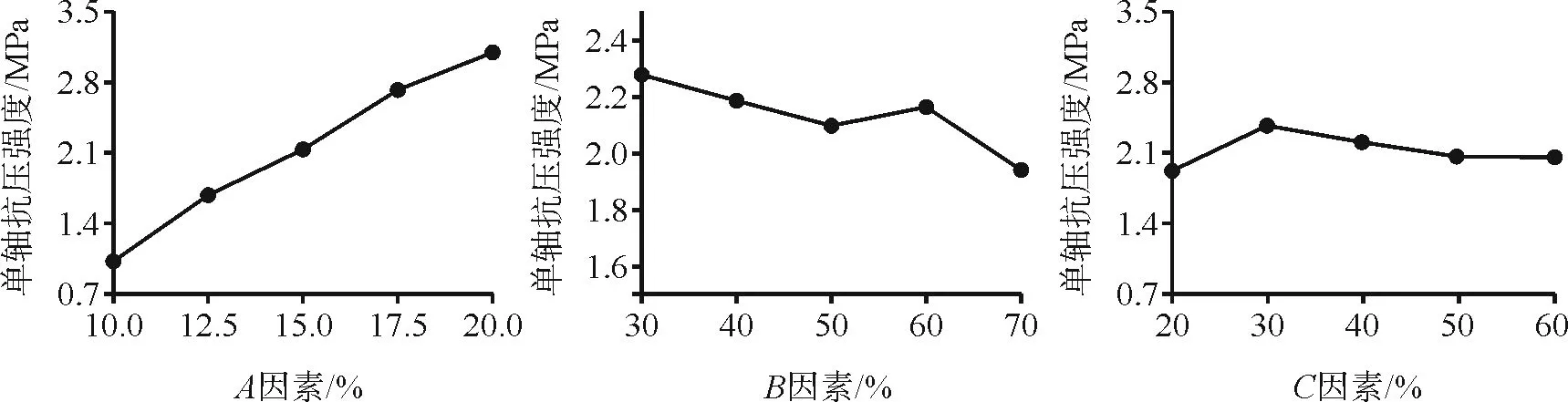
图4 抗压强度的敏感性分析

3.3 抗拉强度影响因素分析

3.3.1 极差分析

将单轴抗压强度的各因素水平的均值通过统计，并且得出各因素的极差，见表6。通过密度的极差分析，可以直观得出各因素的影响程度：A>B>C。并得出：随着胶结剂占总量的比例(A因素)的增加，抗拉强度逐渐增大；随着水泥占胶结剂的比例(B因素)的增加，抗拉强度减小(表8)。

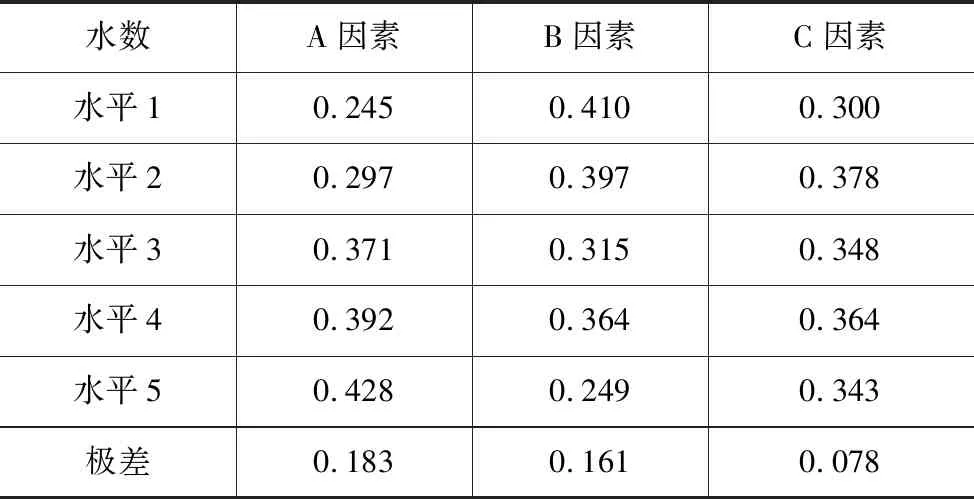
表8 抗拉强度的极差分析 MPa

3.3.2 方差分析

在置信水平α为0.1时，显著性水平F(4,8)=2.81，由表7可知，各因素的显著性比较：A>B>C，A因素对抗拉强度影响非常显著，B因素与C因素对抗拉强度均不显著。考虑到极差分析的结果，可得A因素与B因素对抗拉强度影响都较为显著(表9、图5)。

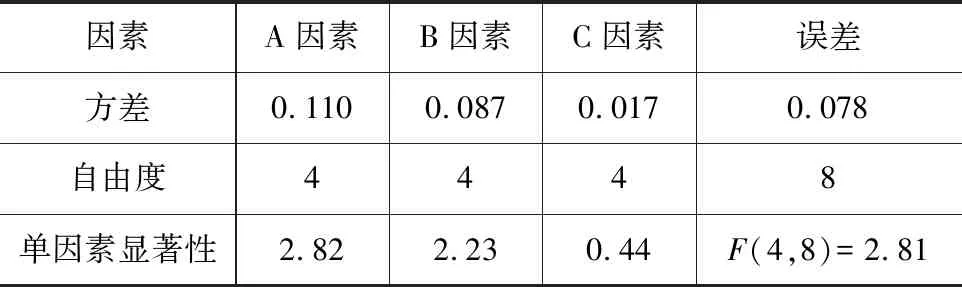
表9 抗拉强度的方差分析

图5 抗拉强度的敏感性分析

3.4 弹性模量影响因素分析

3.4.1 极差分析

将单轴抗压强度的各因素水平的均值通过统计，并且得出各因素的极差，见表。通过密度的极差分析，可以直观得出各因素的影响程度：A>C>B。并得出：随着胶结剂占总量的比例(A因素)的增加，单轴抗压强度逐渐增大(表10)。

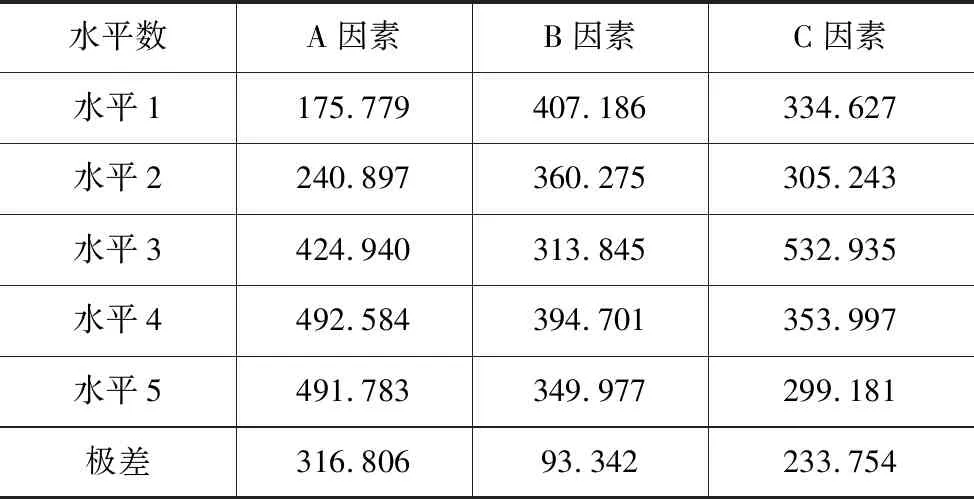
表10 弹性模量的极差分析 MPa

3.4.2 方差分析

在置信水平α为0.1时，显著性水平F(4,8)=2.81，由表可知，各因素的显著性比较：A>C>B，A因素和C因素对弹性模量的影响非常显著，B因素弹性模量影响不显著。与极差分析的结果一致(表11、图6)。

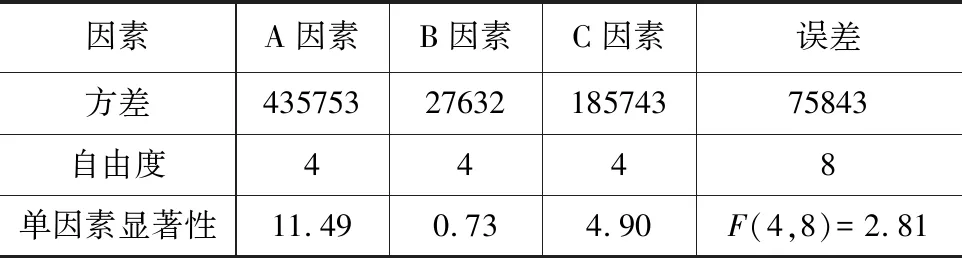
表11 弹性模量的方差分析

图6 弹性模量的敏感性分析

4 结论

本文采用三因素五水平的正交试验，开展了25组不同水平的配样方案，通过单轴抗压试验与劈裂试验，得到了材料的密度、单轴抗压强度、抗拉强度、弹性模量的四种参数。通过正交试验的极差分析和方差敏感性分析，主要得到以下结论：

(1)在各水平各因素的不同配比之下，材料的各参数取值范围较广，密度主要在2.18～2.37 g/cm3，单轴抗压强度主要在0.91～3.52 MPa之间分布，抗压强度在0.21～0.53 MPa之间分布，弹性模量在138～837 MPa之间分布，能达到大部分模型试验中的相似材料参数要求。

(2)试验材料的影响因子中，胶结剂占材料总量的比例(A因素)对各物理参数的影响最大。随着胶结剂占材料总量的比例(A因素)的增加，抗压强度、抗拉强度、弹性模量都呈现不同程度的增长。水泥占胶结剂的比例(B因素)对材料的密度影响较大，密度随B因素呈正相关增长。而重晶石粉占骨料的比例(C因素)对材料的弹性模量影响较大，且呈波动变化，到40 %左右达到峰值。

(3)通过上述研究可知：胶结剂占材料总量的比例(A因素)影响最大，为配比试验的主要控制因素，而水泥占胶结剂的比例(B因素)和重晶石粉占骨料的比例(C因素)为次要控制因素，为今后模型试验相似材料的配比研究具有一定的理论依据。