由对日偏食的简单观测估计日月直径
2020-09-17赵芸赫马宇翰
赵芸赫 兰 鑫 黄 敏 马宇翰
(1. 首都师范大学附属中学,北京 100048; 2. 四川省成都市新都一中铭章学院,四川 成都 610500; 3. 北京计算科学研究中心,北京 100193)
2019年12月26日,由于月亮处于地球和太阳间的特定位置,在全球部分地区出现了日环食现象.本次日环食的环食带,宽约118 km,自沙特阿拉伯开始,经过卡塔尔、阿拉伯联合酋长国等地,至太平洋西部结束.而中国全境并未处于这条带中,因此,在中国境内能看到的是日偏食现象.
利用天文望远镜、单反相机、日食观测镜、以及目前一些智能手机自带的照相机等都可以对日食进行观测和记录.在日食的若干观测方式中,小孔成像简单易行,初中学生便能掌握其原理.通过对该小孔成像的装置进行改进,可以使学生能够更好地探究其成像与像距、孔的大小形状等的关系.将小孔成像的原理运用于日食天象中,学生容易分析出太阳在被月亮遮挡后经小孔可在光屏上成倒立缩小的实像,像距越大,像越大.且所成的像仅与这个“残缺太阳”的形状有关.因此,利用小孔成像的装置来观测日食,对于学生来说是一次很好地对于知识的迁移和应用.另外,除了运用小孔成像原理本身,对于所观测到的日食结果也可以有很多可以挖掘和讨论的.
1 利用小孔成像观测日偏食
当日午间,北京地区天气状况良好,能见度很高.笔者按照计划分别在首都师大附中北校区和北京计算科学中心,利用小孔成像原理对北京地区上空的日偏食现象进行观测.
图1所示小孔成像装置由11个一次性纸杯连接而成,中间打通作为中空镜筒,前部戳一小孔用于透光,尾部用半透明塑料薄膜套封作为观测屏.所用一次性纸杯的高度为85 mm,上口直径为75 mm,从小孔到观测屏的距离d=11×85 mm=0.935 m.从北京时间下午13:30至14:20,笔者用图2所示小孔成像装置观测到的部分偏食图像如图2所示.

图1 观测日偏食用的小孔成像装置

图2 小孔装置成像屏上所观测到的偏食图像
图2中的光亮部分为太阳经过小孔在观测屏幕所成像.可以看出,光亮圆形的边缘处有一缺口,这便是由于月球的遮挡导致的日偏食现象.随着观测的进行,月球所遮挡的部分随着时间先增大后减小,在遮挡部分最大时,遮住的面积约占整体圆形面积的15%左右,与预测的一致.
2 从对日偏食的观测估算日月半径

图3 小孔成像原理示意图
由于偏食的出现是月球和太阳在观测视野中几何上的相互遮挡造成的,故本文通过对偏食的观测结果的分析,利用偏食成像的亮部和暗部的尺寸特征对太阳和月亮的尺寸进行简单估算.小孔成像原理的简单图示如下.
图3中,物体尺寸(直径)为R, 物体到小孔距离为L, 小孔到成像屏距离为d, 物体经小孔在屏上所成像尺寸为r. 根据相似三角形的比例关系,有
(1)

图4 利用PPT的标准圆测量像的直径
将图2中观测到的日偏食图像中一张较为清晰的图片放入PPT处理:分别用标准圆形将观测屏区域和亮斑区域圈中,如图4中两个环形所示.
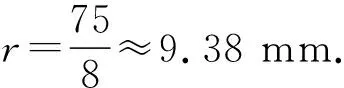
1.5×109m.
(2)
查阅资料得,太阳直径的实际值为R0=1.392×109m.由于观测精度问题,估计值与实际值间相对误差约为7.8%.
下面利用类似的办法来估计月球的直径.在日偏食图像中,太阳所成像边缘的缺口即为月球的影子,因此将边缘所对应的圆形补全即可得到月球的观测直径.设太阳和月亮的实际半径分别为R日、R月,观测半径分别为r日、r月,日地距离和月地距离分别为L日、L月,则根据小孔成像原理,有如下两个比例关系
(3)
消去两式中的孔-屏距d,可以得到
(4)
(4)式中,根据已经估计出的R日≈1.5×109m,以及查资料可知日地距离和月地距离分别为L日=1.5×1011m,L月=3.84×108m(这里采用的是月地平均距离),因此只需要知道太阳与月亮所成像的尺寸比即可得到月球直径的估计值.然而,由于利用小孔成像得到的像边缘较为模糊.为了更好地对月球像的半径进行测量,本文借助图5中由手机和单反相机拍摄得到的图片进行进一步分析.

图5 由手机和单反相机拍摄得到的北京地区日偏食图像

图6 测试月亮半径示意图
同样在PPT中用标准圆形,将图5(b)中的太阳(光亮区域)和月亮(边缘黑色缺角)的完整圆标注出来,分别如图6中的两个圆环所示.
用测量工具得到上图中小圆环与大圆环的直径比约为0.931.将这一结果代入上述关于R月的表达式,我们得到
(5)
查阅资料得月球直径真实值为R月=3.476×106m,则本文对月球直径估计的相对误差约为2.8%.
3 视角约束下的日食形成条件

图7 新加坡上空的日环食现象
在上面的分析中,本文从日偏食的观测结果中分别估计了太阳和月球的直径.如文章开头所介绍的,虽然中国境内无法看到完整的环食现象,但是在环食带的118 km覆盖范围内,可以看到月亮的影子覆盖于太阳正中,如图7所示.
从图7可以清楚地看出,在环食食甚的短暂时间内,月亮的影子处于太阳正中,而只在边缘露出一圈亮环.环食景象中,日月同在,一起形成了如戒指般的图像而悬挂于天空,甚是好看.造成日环食和日全食现象不同的原因其实在于月地距离的差异.在初中物理教学中,日环食和日全食的形成条件是地球分别处于月亮的伪影区和本影区.而之所以3者在运行过程中可以满足这个条件,是由3者间的距离、半径等一系列合适的关系决定的.如何用中学生能够理解的方式来阐述这个关系是值得讨论的.本文将从月亮与太阳对地球的视张角之比的角度来讨论这个问题,从而解释为什么我们恰好能在地球上观测到日环食和日全食两种天象.在图8中给出了日全食和日环食的示意图.
图8中左边圆代表地球,中间圆代表月亮,右边圆代表太阳,实线和虚线所夹范围分别是月球和太阳对地球形成的视张角.在图中,上半部分是日全食,此时月地距离较近,月亮对地球的视张角大于太阳对地球的视张角,因此在地球上看来月亮可以完全遮住太阳;图中下半部分是日环食,此时月地距离较远,月亮对地球的视张角小于太阳对地球的视张角,因此在地球上看来月亮只能部分遮住太阳,而太阳边缘一圈的光可以直接被地球的观察者看到,即看到图8所示景象.

图8 日全食和日环食
从图中可以看出,正是在不同的时期内,地月距离的不同,导致了日环食和日全食的区别.而不同的地月距离差异,是由于月球轨道是一个与标准圆差异较明显的椭圆导致的.查阅资料可知,月球的近地点和远地点的地月距离分别为
L月a=3.63×108m,L月b=4.06×108m.
(6)
当然,地球绕太阳的轨道也不是一个标准圆形,但是由于地球轨道的偏心率很小,故可以忽略日地距离变化带来的影响.若将月球和太阳对地球的视张角分别定义为
(7)
则根据图7的示意,出现日全食的条件为θ月≥θ日,反之出现日环食.由于日地距离、太阳以及月亮的尺寸均可视为恒定值,因此我们有月球和太阳对地球的视张角之比α满足
(8)
代入数据有
0.923≤α≤1.032.
(9)
这一结果十分有趣,表明月亮对地球的视张角与太阳对地球的视张角之比正好在1附近.当0.923≤α<1,出现日环食;而当1≤α≤1.032,日全食将会发生.我们知道,对于两个距眼睛远近不同物体而言,我们所观察到它们的大小由其对观测者所成的视角决定,而不是其绝对尺寸.因此,虽然月亮和太阳距离地球的远近相差甚远,但这一效应恰巧和月亮与太阳的绝对大小的差异互补,从而在地球上的人们看起来,月亮具有和太阳差不多的尺寸,即α≈1.这也是为什么在地球上观察日食现象时,月亮可以差不多正好遮挡太阳的原因.同时,也可以计算出当刚好出现全食、环食现象临界点对应的月地距离约为
L月a=3.746×108m.
(10)
即当满足日食出现条件时,当地月距离处于L月a≤L月≤L月c时,能够看到日全食,而当地月距离在L月c≤L月≤L月b之间时,看到的就是日环食了.这一次所出现日环食现象,意味着当日的月地距离处于后面这一范围.在前文估计月球直径的计算中,本文利用的是月地平均距离.若查到当日附近更准确的月地距离数据,便可以得到更准确的估算结果.
从上面的分析不难看出,月地距离,日地距离,月球半径和太阳半径间的关系是如此的刚刚好,让我们既可以看到日全食现象,也有机会看到日环食现象.如果地月间的距离偏差一点,如月球轨道上任意一点距离地球距离均大于目前的远地点距离,或者均小于近地点距离,那人类便只能看到日环食,或者日全食的单一现象了.这大概就是大自然的鬼斧神工吧.
4 结论
本文利用小孔成像装置及手机等拍摄装置观测了2019年12月26日在北京的日偏食,并依据观测结果估算了日月直径.
另外,本文从月亮与太阳对地球的视张角之比的角度,解释了恰好能在地球上观测到日环食和日全食两种天象的原因.
