基于折射定律对透镜成像的理论计算及近似处理

赵清锋

(武汉市卓刀泉中学建和分校，湖北 武汉 430065)

透镜成像是几何光学的重要内容，在照相机、投影仪、显微镜、望远镜等相关光学系统的研究中也是基础，在《光学》教材中通常结合费马原理对透镜成像关系进行计算给出对应公式的高斯形式.[1-3]这种理想模型只能初略地分析简单的光学系统和确定成像的大致位置，对于生活中的光学系统需要准确的计算并加以修改设计从而达到更好的应用价值.在相关几何光学书籍中多以单个折射面进行准确计算.[4,5]基于折射定律，首先对透镜成像中二维模型进行理论计算，得出了准确的物像关系公式，并与近似计算结果进行了比较，同时作图分析了球面透镜像差的特点；然后根据准确物像关系，在忽略微小量的近似处理条件下得到透镜物像关系近似公式，比高斯形式要简单，而且适用于任意介质；在薄透镜中认为hA=hB，给出近轴条件下薄透镜的物像关系公式，与薄透镜的高斯公式完全一致.

1 透镜物像关系公式的准确形式

透镜的两个曲率半径分别为r1和r2的折射球面组成，透镜的厚度为d，透镜左侧和右侧介质的折射率分别为n1、n2，透镜的折射率为n.若在主轴上有一点光源P，发出的一条光线PA经透镜折射后，交于主轴P′点，与透镜左侧右侧的交点分别为A和B，初始条件已知θ2(或hA)、θ(或者-l1)，其余对应符号如图1所示.

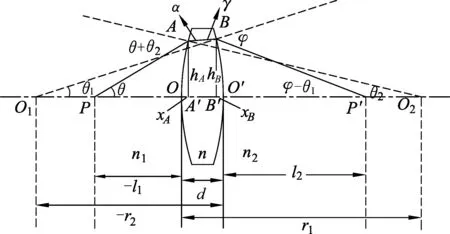
图1 透镜成像的几何关系

由以上条件根据几何关系可得

(1)

上式根据和差化积化简约分并利用几何关系α+γ=θ1+θ2，可得

sinγ=sin(θ1+θ2-α)=

(2)

像所在的位置

(3)

同理可得物所在的位置

(4)

联立(3)、(4)两式即可到准确的物像关系公式如下

(5)

此式给出的单个透镜的准确物像关系，而一般书籍中给出的均由单个折射面对成像系统分析，[4，5]借助数值模拟作图在分析几何相差直观形像，以《光学教程》第199页关于厚透镜像所在位置的例题为例，[1]根据(5)式得到的像方截距与高斯公式得到像方截距如图2所示.

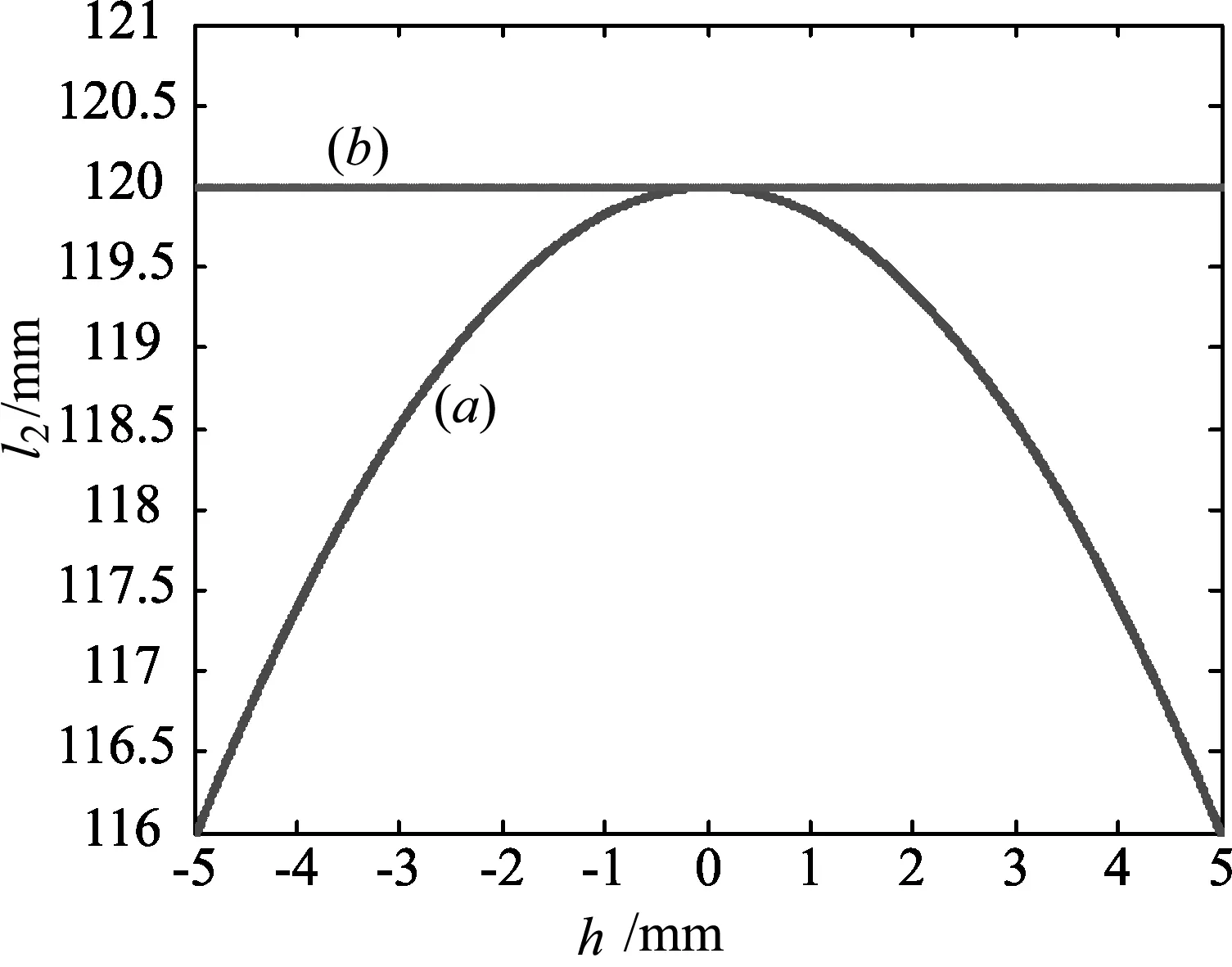
图2 像方截距l2随入射高度h的奕化关系

其中r1=60 mm，r2=40 mm，d=20 mm，l1=80 mm，n1=n2=1.5，n=1.曲线(a)为本文关系式(5)所得像方截距l2随入射光线离轴距离h的变化关系，在离轴距离为-5 mm～5 mm之间，像方截距在116 mm～122 mm之间，并不在确定的某一点；直线(b)为高斯物像关系公式所得结果为120 mm.从图2中可以看出本文计算结果存在球差，离轴越近与书本理论计算结果越接近，离开透镜后的光线如图3所示.

图3

从图3可以看出光线经过透镜后会聚于某一点附近，在粗略分析透镜成像问题可用(5)式数值计算；但将横坐标缩小到116 mm～122 mm之间光线并不完全会聚一点(如图4)，根据弥散斑的概念应取118 mm，这对初学光学设计的学生可以进行数值分析直观有效.

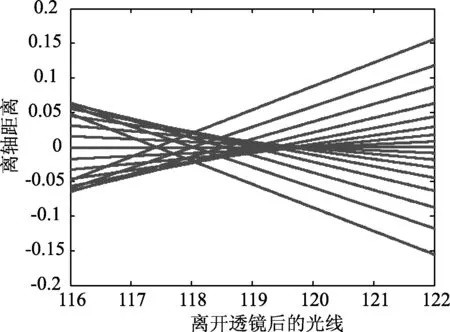
图4

2 近轴条件下透镜物像关系的近似处理

在近轴条件下的薄透镜可以认为sinx≈x；xA、xB≪-l1、l2、-r2、r1；-l1θ≈r1θ2≈hA；-r2θ1≈hB，利用以上近似处理(5)式化简为

l2·(φ-θ1)=hB.

(6)

(7)

将-l1θ≈r1θ2≈hA，-r2θ1≈hB代入上式化简可得

(8)

由几何关系近似可得

(9)

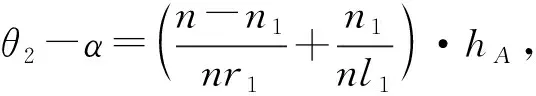
(10)

将(10)式代入(8)式即可得到近轴条件下的透镜物像关系

(11)

(11)式所描述的透镜物像关系公式对薄透镜和厚透镜均能使用，对于薄透镜计算结果更精确，而且适用于任意介质.当n1=n2=1时，上式可简化为空气中厚透镜物像关系公式，经过一定的转换，可以得到与厚透镜物像关系高斯公式的原始形式一致，[1]但本文中所提出的公式明显更简洁适用，而且对任意介质均能使用.

若为薄透镜，可以认为hA=hB，则(8)式可以化简为近轴条件薄透镜物像关系公式，与高斯公式一致.

(12)

在相关文献和书籍中，薄透镜的物像关系多以费马原理推导.[2，3]本文借助折射定律中几何关系推导结果与费马原理推导的结果一致，可为初学者提供更多的思路.