基于CHNN的自动化立体仓库货位优化研究

赵 钰 叶 飞 骆星智 陈嘉羽 杨飞龙

(1. 国网安徽省电力有限公司， 安徽 合肥 230061；2. 国网安徽省电力有限公司 物资分公司， 安徽 合肥 230061)

伴随物流业的高速发展以及现代工业智能制造进程的快速发展，自动化立体仓库逐渐兴起，通过计算机技术、信息技术和控制技术的综合应用使得货物存储、物流管理的效率大大提高，成本逐渐降低，不断增强了企业的竞争力。自动化立体仓库的研究吸引了很多专家学者的研究兴趣[1-3]，为进一步提高存取货物效率，节约资源成本，货位优化问题变得很有意义。目前国内对于立体仓库货位分配问题的研究，较多采用遗传算法[4]、禁忌搜索算法[5]，粒子群算法[6]等，鲜有使用神经网络处理货位分配问题。利用神经网络解决组合优化问题是神经网络应用的一个重要方面，本研究拟采用连续Hopfield网络(Continuous Hopfield Neural Network，CHNN)对货位分配组合优化问题进行研究，并给出有效的优化算法，最后通过Matlab仿真验证货位分配组合优化算法的有效性。

1 货位分配数学模型

自动化立体仓库的规模根据实际需要会有不同的格式尺寸，在本研究中不妨设货架共有p排，m列，n层。如图1所示，其中货架共有8排8列。

图1 货架和堆垛机初始位置平面示意

为讨论方便，在货位建模前给出如下假设：(1)堆垛机所占空间忽略不计，出入库起始位置在出入端口为坐标原点；(2)堆垛机水平运行速度和垂直运行速度保持不变；(3)堆垛机取放货所用时间忽略不计，一次只能存或取一个货箱；(4)存放货箱的货格为正方体，上下、左右相邻的货箱之间距离相同；(5)货物周转率和平均库存已知。

一些主要变量定义如下：相邻正方体货箱之间的几何中心距离为d0；(x,y,z)表示第x排y列z层上货格对应的货位坐标，x=1,2,…,p，y=1,2,…,m，z=1,2,…,n；vl表示水平方向上堆垛机的运行速度，vh表示竖直方向上堆垛机运行速度；第i类货物的周转率为si和平均库存为qi。

为保证存取货物整洁有序，本研究考虑按货物品类进行分类存取，通过计算周转率和平均库存的乘积siqi，按其值大小来确定分配给不同种类货物的货架，将乘积值最大的那类货物的存放安排在离堆垛机出入口最近的货架1，次之安排在货架2，其余安排以此类推。按此种方法分类，则乘积siqi与x取值有对应关系，既siqi取值最大时对应x=1，siqi取值次之时对应x=2，以此类推。此外设货物种类数小于等于立体仓库的总排数。

在立体仓库中存取货物的时候力求花费时间最短，仓库货架稳定性较好，这也是本研究要考虑的两个优化目标。由于按照上述货品分类方法，确定货品种类就意味着确定了货格坐标(x,y,z)中的第一分量x，因此后续讨论中的优化问题仅需要考虑怎样来确定货格坐标(x,y,z)中的第二分量y和第三分量z，问题可以简化到只考虑单个货架的优化存储问题，也既仅需要讨论如何采取最优方法将某类货物存放到单个货架中的某列某层。

1.1 存货时间耗时分析

将某类a件货物存放到某单个货架中的总耗时为

(1)

存货时间耗时最优化问题表示为

(2)

1.2 堆货稳定性分析

货物放到货架上具有的势能越小，则稳定性越好，将a件货物放到货架上的总势能为

(3)

货物存放到货架上的总势能的最优化问题表示为

(4)

存放货物既要考虑存放货物耗时最短，还要考虑存放货物的总体稳定性最好，则所讨论的货物存放最优化问题即为多目标最优化问题。如果单独求解各个最优化问题，所得结果必然不一致，就会给讨论的问题带来很大麻烦。现在利用权重将两个单独的最优化问题合并成多目标组合最优化问题，如下所示：

minf(y,z)=αminta(y,z)+

(1-α)minpe(y,z)，

(5)

其中α∈(0,1)，也既

(6)

α∈(0,1)，权值α的不同取值代表着在货物存放多目标最优化问题中，更侧重于减少存货耗时还是更侧重于保证货架稳定性。权值α相对大些，则更侧重于减少存货耗时，反之则更侧重于保证货架稳定性。

2 算法设计

2.1 模型映射

Hopfield神经网络是单层对称全反馈网络，根据激活函数选取的不同，可分为离散型Hopfield神经网络(DHNN)和连续型Hopfield神经网络(CHNN)。DHNN主要用于联想记忆，CHNN主要用于优化计算。由于CHNN由n个神经元并联组成，且以模拟量作为网络的输入输出量，所以它在信息处理的实时性、协同性、分布存储等方面更接近于生物神经网络。

将某类货物存放到某m列n层的单个货架中，需要使用m×n个数据表示货架中的货格存放货物情况，这些数据可以使用m×n矩阵来表示，m×n矩阵中某一个元素为1表示对应货格存放一个货物，某一个元素为0时表示对应货格不存放货物。为处理立体仓库货位优化问题，需要将货位优化问题映射为一个Hopfield神经网络的动态过程，对应于m×n矩阵来表示货架中货格是否存放货物，需用m×n个神经元来实现，神经元仅输出1或0，分别表示对应货格存放货物或不存放货物。

2.2 构造Hopfield神经网络的能量函数和动态方程

人工神经网络常利用渐进稳定点来解决一些问题，Hopfield神经网络的稳定性可以用能量函数进行处理，如果把系统的稳定点视为一个能量函数的极小点，把能量函数视为一个优化问题的目标函数，那么从初态朝这个稳定点的演变过程就是一个求该优化问题的过程。这样的优点在于它的解并不需要真的去计算，而只要构成这种反馈网络，适当的设计其连接值和输入就可以达到目的。Hopfield神经网络能量函数的物理意义就是在那些渐进稳定点的吸引域内，离吸引点越远的状态，所具有的能量越大，由于能量函数的单调下降特性，保证状态的运动方向能从远离吸引点处不断地趋于吸引点，直到达到稳定点。

文章构造的CHNN能量函数包含优化目标项(6)，此外将存放货物总量a构成约束项也包含进CHNN能量函数中，则连续Hopfield神经网络的能量函数可表示为：

(7)

其中(7)式前两项为目标项，最后一项为约束项，A,B,C为适当常系数。

网络的动态方程可表示为：

(8)

(9)

其中u0为uij初始值。

2.3 优化计算

步骤1 网络初始化后，利用式(8)和欧拉公式计算

步骤2 利用式(9)计算vij(t)；

步骤3 利用式(7)计算能量函数E；

步骤4 判断迭代是否结束，结束则终止，否则返回步骤1。

3 实例仿真

考虑一个单排货架有5层7列，要存放13个货物。堆垛机从初始待命点运行到第1列至第7列所用时间用向量表示为

tr=[1,2,3,4,5,6,7]。

由地面导轨运行到第1层至第5层货架中心所用时间用向量表示为tl=[0.5,1.5,2.5,3.5,4.5]。第1层至第5层货物所具有的势能用向量表示为Ep=[1,2,3,4,5]。使用MATLAB仿真，取u0=0.02，迭代次数K=1 000，步长ΔT=0.000 1，A=100，B=1，C=1 000，考虑以货架稳定为主取参数α=0.3，货物堆放货架情况如图2所示，能量函数随迭代过程变化的曲线如图3所示。

考虑以运行时间为主取参数α=0.7，货物堆放货架情况如图4所示，能量函数随迭代过程变化的曲线如图5所示。

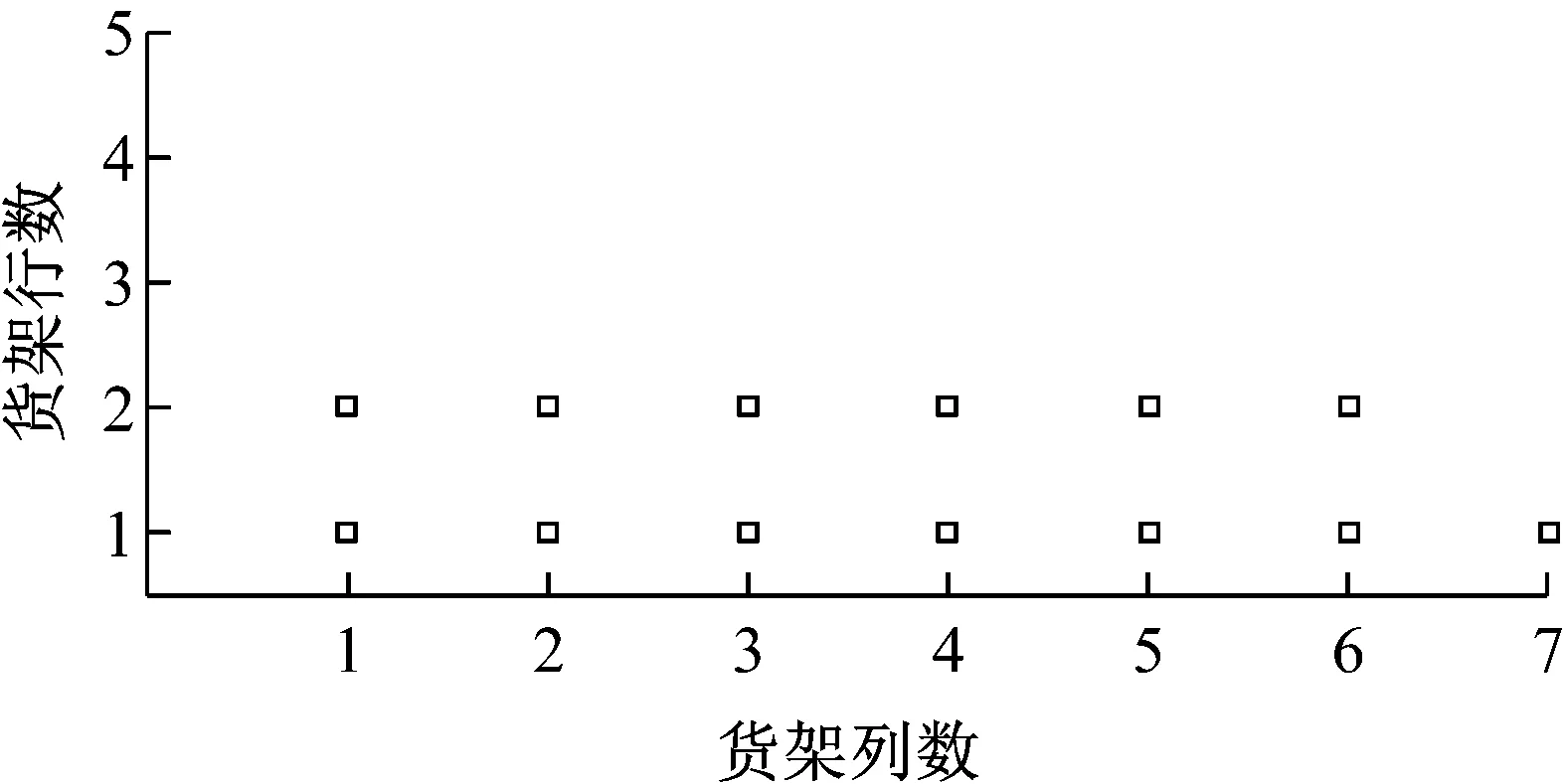
图2 α=0.3时，优化后货物堆放货架情况

图3 α=0.3时，能量函数随迭代过程变化曲线

图4 α=0.7时，优化后货物堆放货架情况

图5 α=0.7时，能量函数随迭代过程变化曲线

通过上述仿真验证了算法的有效性，但是也应注意到参数选择对结果影响明显，而这些参数也没有可遵循的选择规律，实际处理需要多次凑试选择。此外，神经元输出状态同时受到迭代过程中双曲正切S型函数特性及参数选择的影响，有时会出现个别神经元输出状态达不到1的情况。

4 结语

目前国内对于立体仓库货位分配问题的研究，大多采用遗传算法、禁忌搜索算法，粒子群算法等，鲜有使用神经网络处理货位分配问题。利用神经网络解决组合优化问题是神经网络应用的一个重要方面，本研究通过设计CHNN神经网络的能量函数与货位分配组合优化问题相对应，当CHNN神经网络的输出状态趋于平衡点时，能实现货位分配组合优化问题的最优解，并通过实例仿真验证了算法的有效性。此外，也应注意到能量函数、网络参数对优化结果影响较大，不同参数的选择可能会使系统仅达到次优解，或使得系统没有可行解。