基于滑移率的汽车纵向动力学轮胎建模

（陕西工业职业技术学院汽车工程学院 陕西 咸阳 712000）

引言

轮胎作为连接车身与路面的唯一部件，具有支承汽车重量；汽车在不同的行驶工况下，轮胎对路面的冲击进行缓冲；为车辆前进和制动时提供附着力；同时在转向操纵与方向稳定性方面还起到一定的作用[1]。在汽车行驶过程中，车辆的受力情况除了空气阻力之外，其他外力几乎都是与路面的作用而产生的。而轮胎作为路面与车身的连接物，其力学特性对车辆的其他性能至关重要。所以车辆动力学模型和轮胎动力学模型的研究对整车的性能研究有着重要的意义[2]。

轮胎模型作为研究整车模型的关键点之一，必须与车辆模型的精度相匹配。但轮胎的复杂结构与其非线性的力学特性，对于能够研究出高度吻合接近真实力学特性的轮胎模型是一个亟待解决的关键难题之一[3]。

1 车辆纵向力学模型

轮胎模型与车辆纵向动力学模型是整车动力学模型中的主要模型，纵向动力学模型输出的轮胎受到的垂直载荷和车速作为轮胎模型的输入，最终轮胎模型输出的轮胎受到地面的切向力Fx和轮胎的转速ω 又返回到纵向动力学模型中[4]。

1.1 汽车前后轴纵向力建模

汽车在斜坡上时受力如图1 所示。其中β 为倾斜角，m 为汽车质量，A 为迎风面积，h 为质心高度，a、b 为质心距前后轴的距离，Fxf，Fxr为汽车前后轴纵向力，Fzf，Fzr为汽车前后轴垂直力，Fd为空气阻力。

汽车的运动是由所有作用在汽车上的力和力矩决定的。纵向轮胎力推动车辆向前或向后移动。在质心点处，汽车受到重力mg。根据斜坡的倾斜角度不同，重力可能使汽车停在地面上或是使汽车向前或向后运动。无论汽车如何运动，空气阻力的作用都是阻碍汽车运动。为了简化，假设空气阻力通过质心。根据汽车在斜坡上的受力情况，结合运动学和动力学的知识，可列出如下方程。

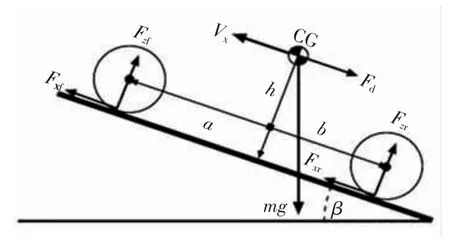
图1 车辆受力模型图

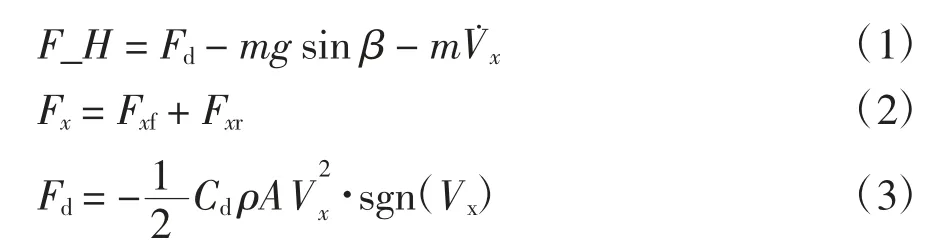
式中：sgn（Vx）是符号函数，当Vx>0 时其值为1，当Vx=0 时其值为0，当Vx<0 时其值为-1。根据方程在Matlab/Simulink 中进行建模，可得到如图2 所示的模型。

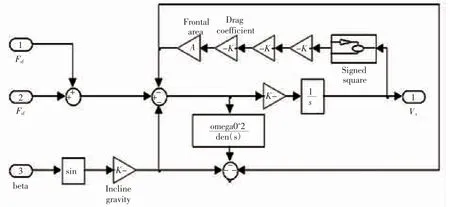
图2 汽车前后轴纵向力学模型

该模型通过仿真得到车速，仿真完成后得到车速波形图如图3 所示。

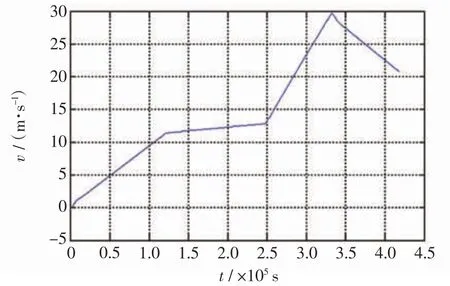
图3 车速输出波形图

1.2 汽车前后轴垂直力建模

根据相关汽车理论知识，由于此时汽车在垂直方向没有加速，忽略旋转质量惯性阻力偶矩以及忽略滚动阻力偶矩之后，对Fzr延长线与Fd延长线交点取矩，得：

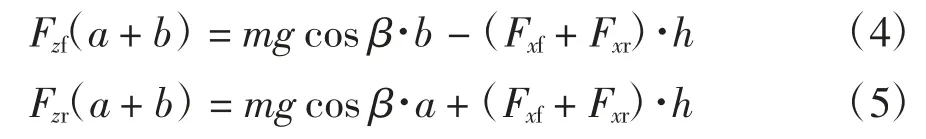
汽车前后轴的垂直力简化为:

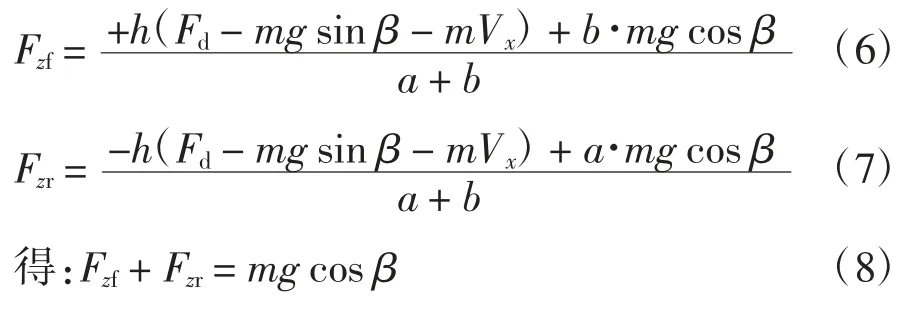
令F_H=Fd-mg sin β-mV˙x得到汽车前后轴垂直力模型，如图4 所示。

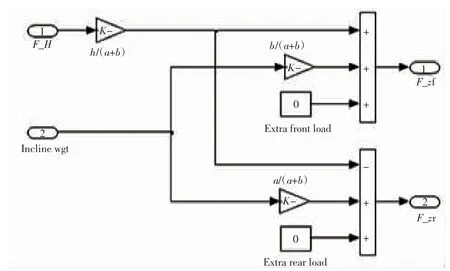
图4 汽车前后轴垂直力模型

通过仿真得到汽车前后轴垂直力波形如图5 所示。

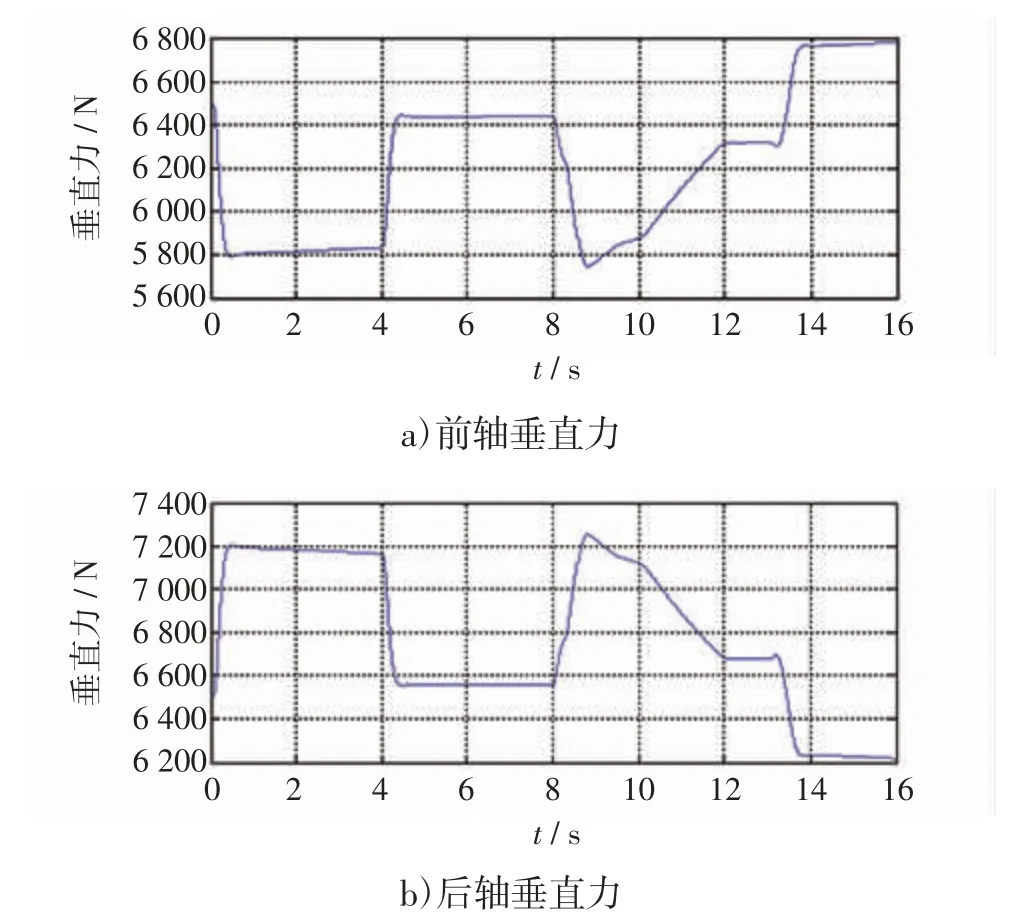
图5 汽车前后轴垂直力

2 轮胎建模

轮胎模型和纵向动力学模型组成了整车模型的主要部分，纵向动力学模型输出的轮胎受到的垂直载荷Fz和车速Vx作为轮胎模型的输入，而轮胎受到的地面切向力Fx与轮胎的转速ω 作为输出，轮胎模型如图6 所示[5]。

该轮胎模型模拟了一个与道路接触的复杂的刚性车轮。并且该模型没有轮胎的外倾、旋转和横向运动，只模拟了轮胎的纵向运动，轮胎受力图如图7 所示。

以下列出了轮胎建模所需要的参数：

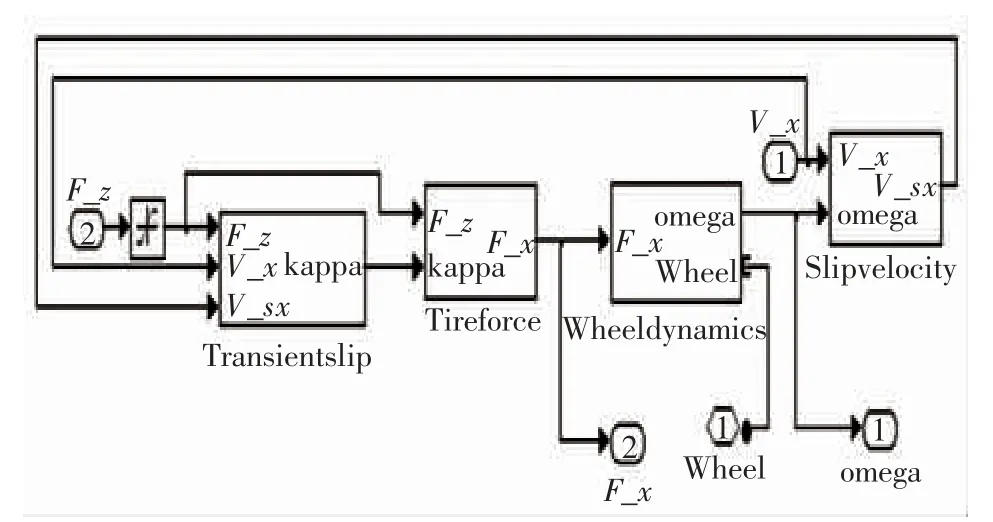
图6 轮胎模型

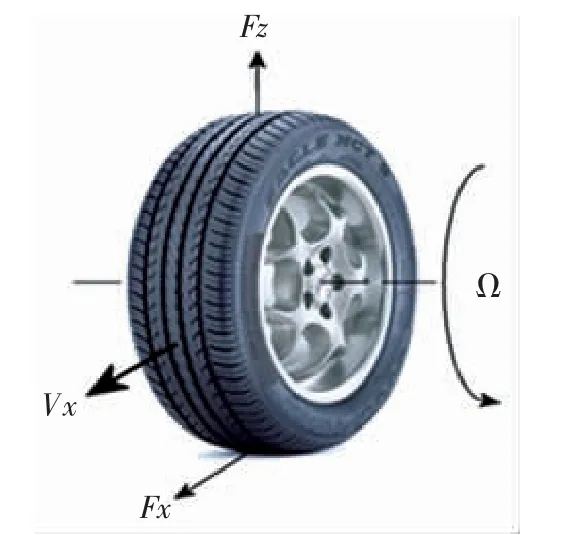
图7 轮胎受力图

re-有效旋转半径；Lw-轮胎总成转动惯量；Tdrive-车轴施加给车轮的转矩；vx-轮心处的纵向速度；Ω-车轮旋转角速度；Ω′-接触点的角速度；Vsx=Vx+reΩ-车轮的滑移速度；-接触点的滑移速度；K=-Vsx/|Vx|-车轮滑移率；K′=接触点的滑移率；u-轮胎纵向变形；Fz-轮胎的垂直负载；Fx=f（K′，Fz）-轮胎接触点的纵向力，也是轮胎的特征函数；-轮胎的纵向刚度；/（CFX）-轮胎的松弛长度。

2.1 轮胎滑移速度模型

如果轮胎是刚性的并且不滑动[6]，则有vx=re*Ω。但是实际情况中，即使是刚性的轮胎也会打滑，并在轮胎的滑移方向产生了纵向响应力Fx。车轮滑移速度vsx=vx-reΩ≠0。车轮滑移率K=-vsx/|vx|。车轮抱死作纯滑动，则K=-1，纯滚动，K=0。

即车轮速度低于车身速度时，轮胎和路面之间会产生滑移，滑移速度vsx是由输入车轮的角速度Ω和轮心的纵向速度vx得到的，具体方程如下：

vsx=vx-reΩ

根据方程所建立的模型如图8 所示。

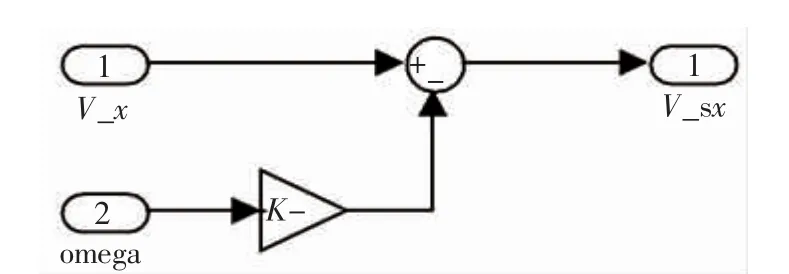
图8 滑移速度模型

通过仿真得到滑移速度波形如图9 所示。

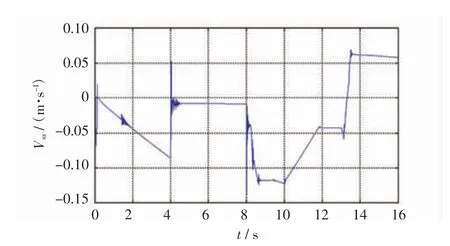
图9 滑移速度

2.2 轮胎接触点滑移模型

以Fz，Vx，Vεx作为该模块的输入，最终可以得到滑移率K′。由于轮胎的变形，所以在接触点处存在略微不同的角速度Ω′。接触点滑移率其中，轮胎变形u 和接触点滑移率满足关系：，该模块是为了显示出Fx对滑移的瞬间反应。

轮胎模型考虑了瞬态和稳态的不同，因而适用于从出发到停止的所有工况。轮胎模型提供了一个稳态轮胎特征函数Fx=f（K′，Fz）

接触点滑移率K′取决于变形u，纵向力Fx是大致正比于垂直载荷Fz的，因为Fx是通过接触摩擦和法向作用力Fz产生的，由于轮胎的变形和滑移所以此关系是非线性的。因为轮胎是滚动的，不处于一个稳定状态，接触点滑移率K′和变形也不是恒定的。在这个模型中，Fx对u 和u 对K′的关系是线性的：

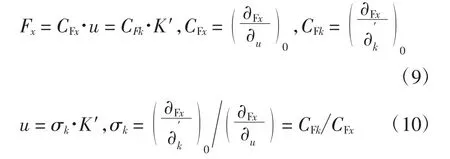
这些属性是取自实证轮胎数据，根据变形u 和接触点滑移率的关系方程推导出：

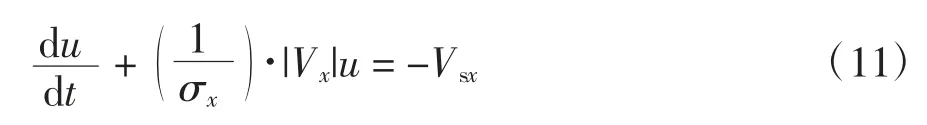
联立上述方程，最终得到下列方程：

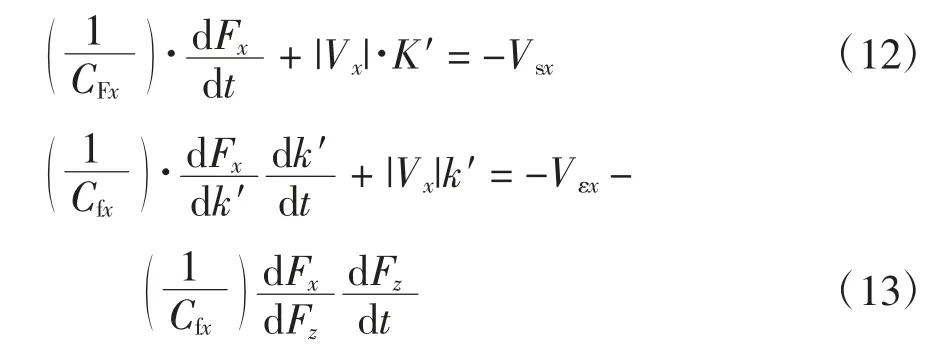
因此，根据方程所建得的模型如图10 所示。

由该模型得到未经修正的滑移率波形如图11所示。

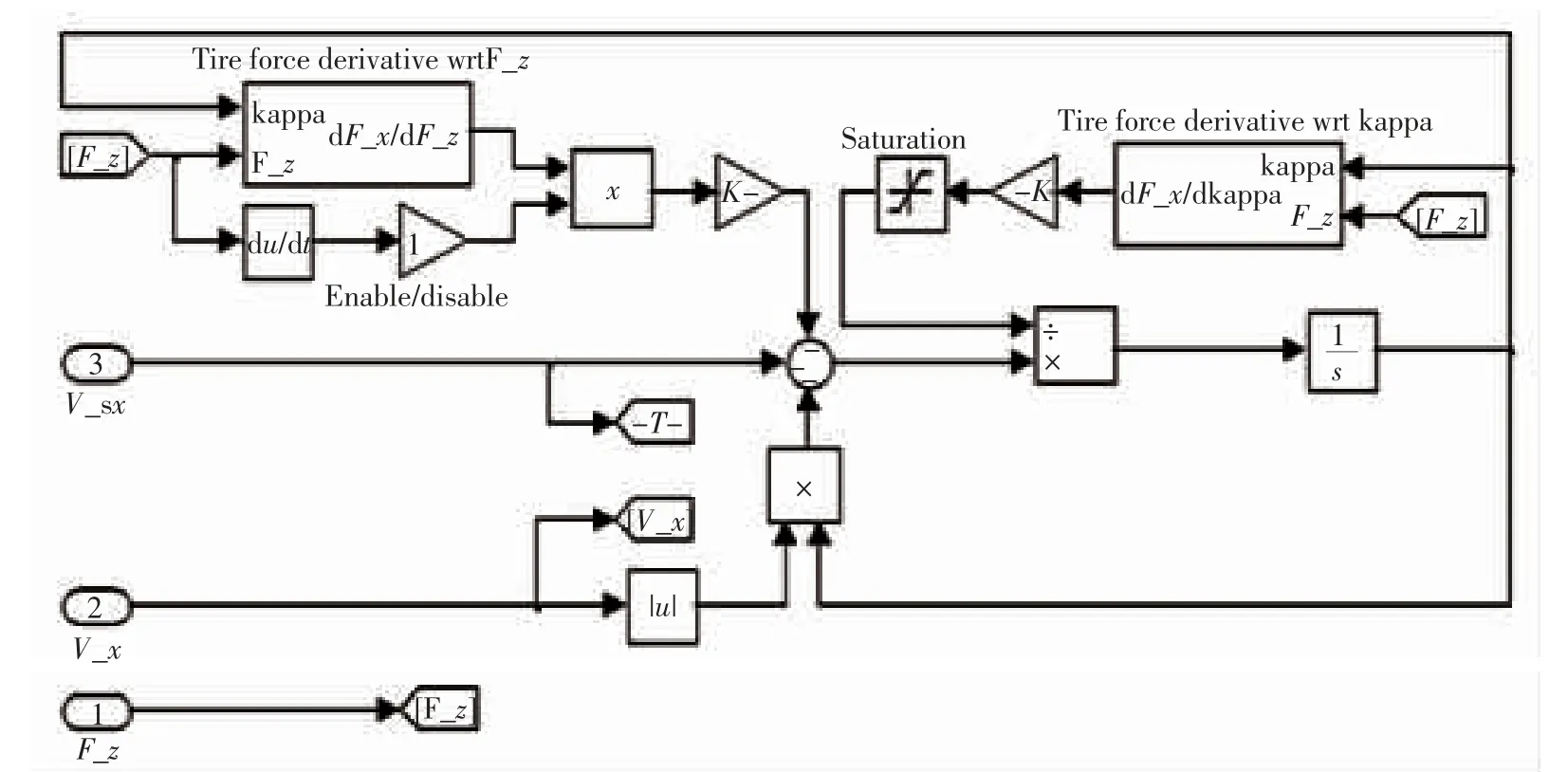
图10 轮胎接触点滑移率模型

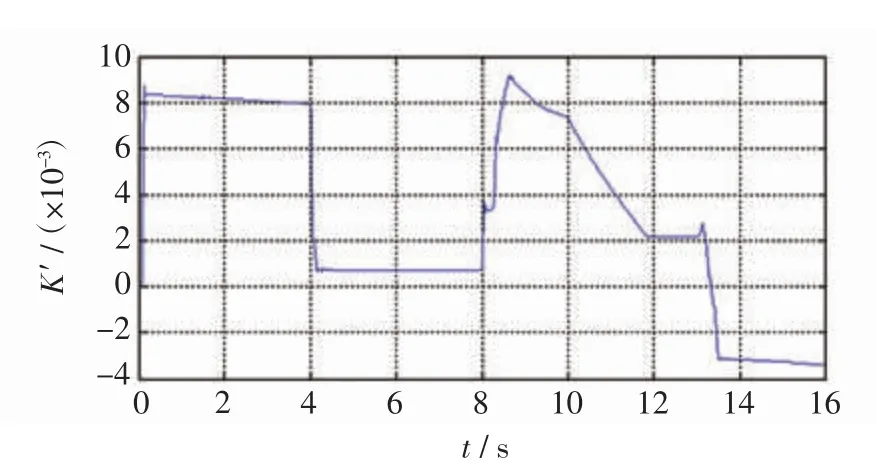
图11 轮胎接触点滑移率

2.3 低速下滑移率修正模型

在高速的时候，轮胎就像一个阻尼器，纵向力只由轮胎滑移来确定；在低速的时候，当轮胎开始运动或是减速直至停止运动时，轮胎更像是一个可变形的圆形弹簧[7-8]其刚度为CFx；在这个极限点上，如果阻尼没有明确地被包含在内，与接触点的滑移率K′和轮胎变形u 相关的线性估计值会变得异常，而这个关系可以被修正为：

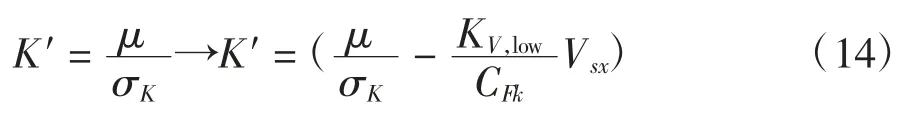
其中从零速平稳过渡时KV，low满足：

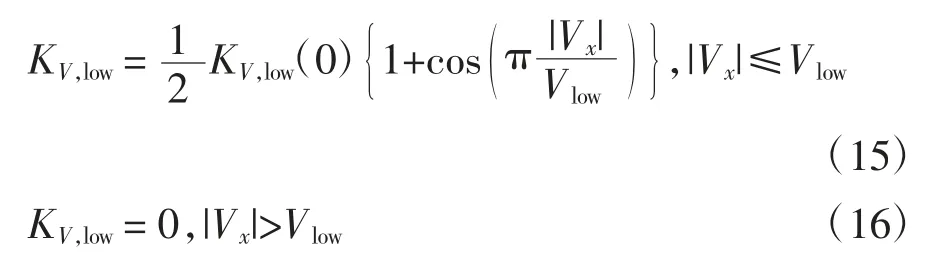
根据方程得低速轮胎的滑移率如图12 所示。

最后将轮胎接触点滑移率模型与低速轮胎滑移率模型结合则得到瞬间滑移模型如图13 所示。

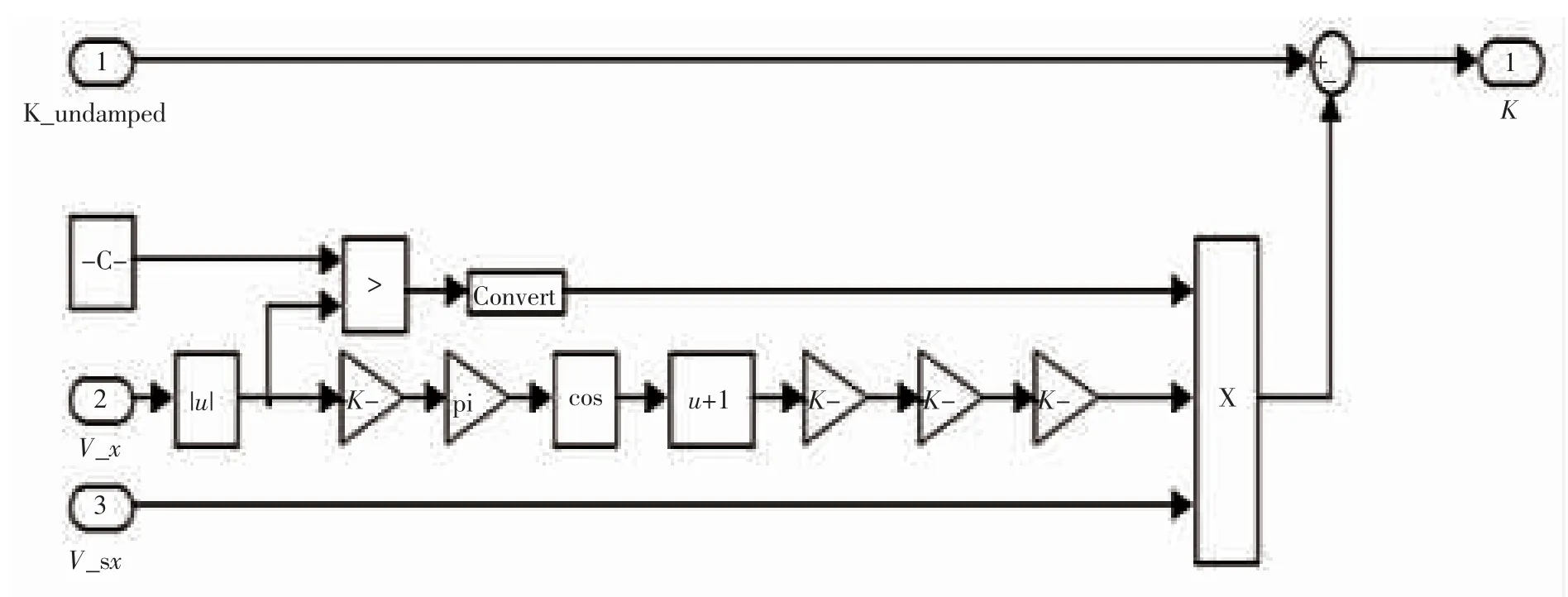
图12 低速轮胎滑移率模型

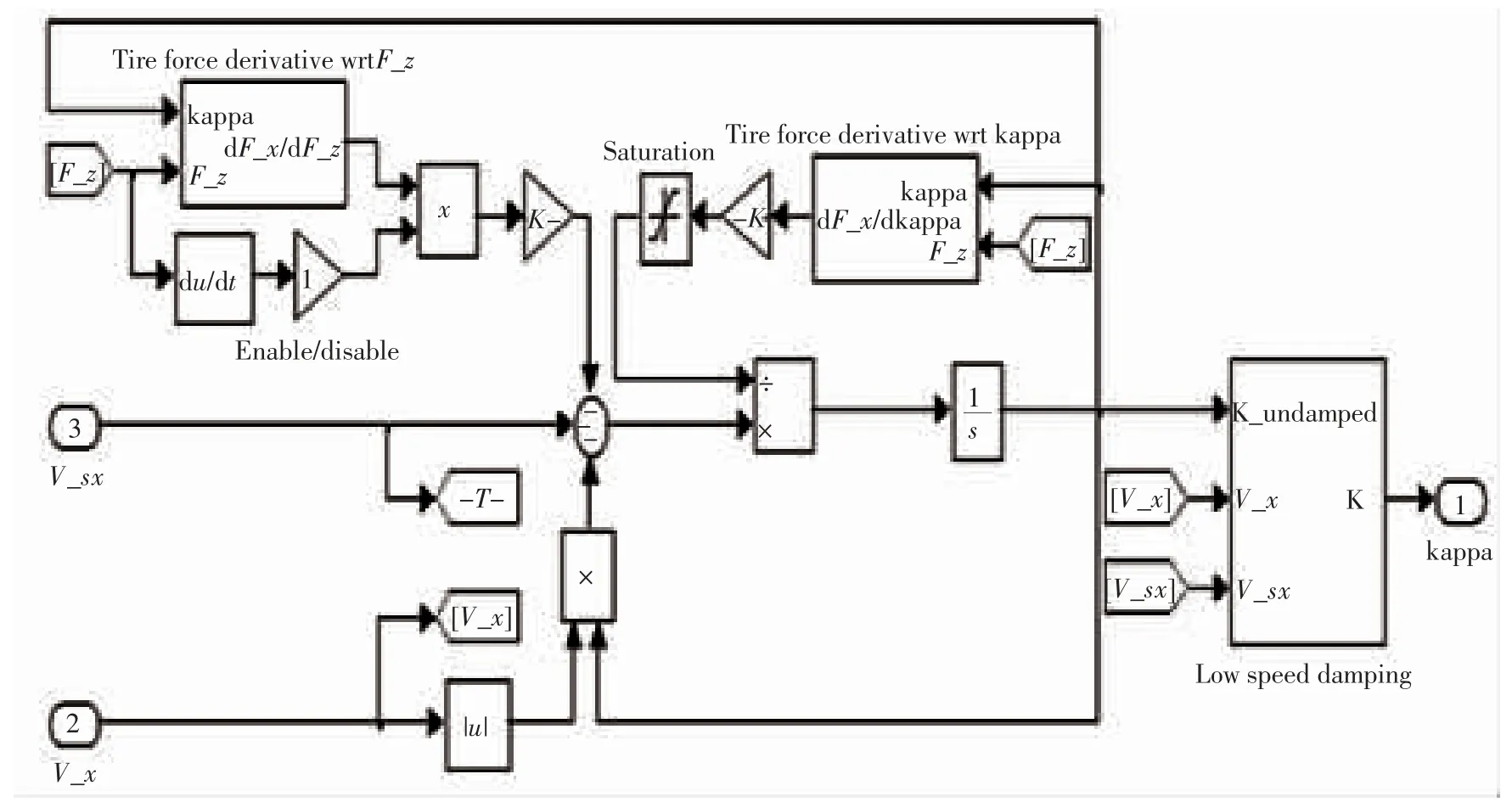
图13 瞬间滑移模型

3 轮胎受力模型

3.1 轮胎纵向力学模型

该模块根据轮胎的特征函数三维图，输入轮胎垂直力Fz和滑移率K，得到轮胎所受纵向力作为输出,利用Matlab/Simulink 建模如图14 所示。

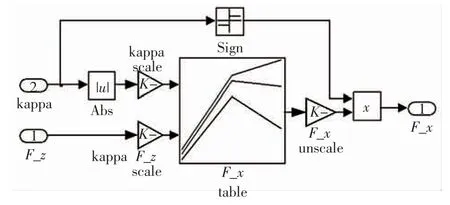
图14 轮胎受力模型

得到汽车所受纵向力如图15 所示。

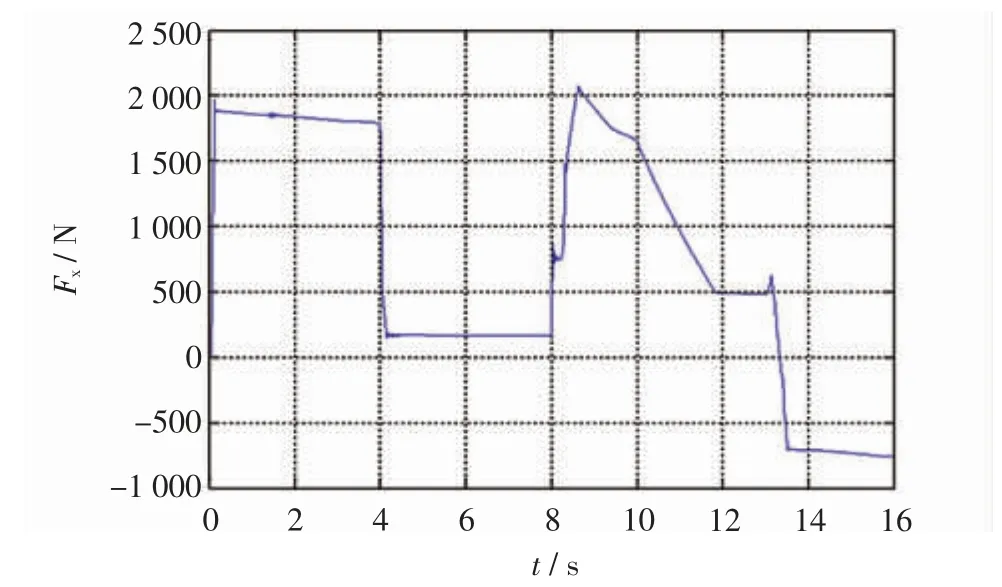
图15 轮胎纵向力

3.2 轮胎动力学模型

该模块中使用了转矩助动器和运动传感器。将由接触点的纵向力Fx产生的力矩作用于转矩助动器，使之激励传动轴产生运动，再利用运动传感器模块，该模块能够将传动轴的运动转化为具体的运动输出信号，如角度，角速度和角加速度[9]。所以可以得到所需要的车轮旋转角速度Ω，建模如图16 所示。

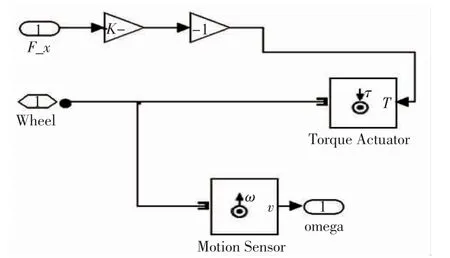
图16 轮胎动力学模型

仿真后得到轮胎旋转角速度如图17 所示。

最后将以上各个子模块连接起来，则得到了轮胎模型。

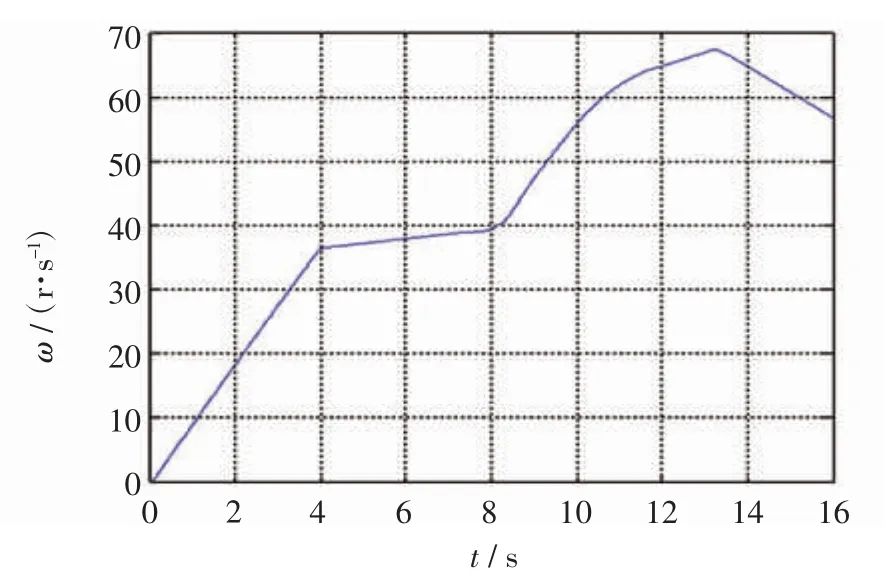
图17 轮胎旋转角速度

4 结论

1）在汽车动力学相关理论指导下建立了车辆纵向动力学模型，并利用Matlab/Simulink 软件进行建模仿真得到车辆速度及前后轴载荷。

2）根据所得车辆速度及前后轴载荷建立轮胎模型，并分析了不同条件下的轮胎子模型。

3）轮胎模型作为整车纵向力学模型的关键部分，对轮胎的不同条件下的滑移情况进行研究，为后续的车辆操控性、稳定性以及车辆行驶制动、轮胎磨损等研究具有一定的参考意义。