基于可靠性的道路运输车辆维护周期优化效果评价研究
2020-09-17徐双应
朱 荣 徐双应
(1-陕西工业职业技术学院汽车工程学院 陕西 咸阳 712000 2-长安大学汽车学院)
引言
道路运输车辆整车制造企业在编制车辆维护手册时,在遵循部分陈旧的国家标准框架之下,需要考虑车辆在不同使用地区的使用条件不同,节省保修成本以及增加售后营收,因此在手册中给定的维护周期相比欧美日等汽车工业发达国家趋于保守。而在《道路运输车辆技术管理规定》(以下简称1 号令)执行前,道路运输车辆技术管理和维护周期均由地方交通运管部门负责。道路运输企业在地方交通运管部门监管下,不得不严格遵循厂家的规定进行维护[1]。1 号令第四条明确道路运输车辆技术管理的责任主体是道路运输经营者;第十六条明确车辆维护周期由道路运输经营者自行确定[2]。因此,对原有车辆的维护周期进行优化,若优化后效果良好,可使道路运输经营单位在保障运输车辆技术可靠的前提下,节省维护和修理成本,提高营运时间[3]。
1 国内维护周期优化效果评价现状
目前,国内专门针对车辆维护周期优化效果评价研究的文献著作尚无。只有少量具有代表性的文献在维护周期优化研究过程中涉及到维护周期优化效果评价。闫长代等[4]通过控制维护和小修费用最低,来优化维护周期,并通过经济分析法来验证了维护周期优化后的效果。孙克亮[5]针对一级维护周期优化,设定了维护周期间隔里程试验,统计不同试验期内车辆的维护和突发性故障小修费用,再利用线性回归分析法,确认最优一级维护周期。徐安等[6]基于考虑定期检测诊断并使车辆维修费用最低的维护周期模型、使车辆运行与维修费用最低的维护周期模型,利用78 辆商用车历史运行数据,求出理论最优维护周期,并通过维护周期里程对比试验验证,确认最优维护周期对应的单位行程的检测和维修费用最低。朱荣[7]基于启发式算法计算最优维护周期,并通过车辆小修频数和小修频率来评价维护周期优化效果。基于以上可知,现有文献涉及到的维护周期优化效果评价方法有两种:一种是基于经济法,通过小修、维护、检测等经济成本来进行评价;另一种是基于车辆可靠性,借助于车辆故障数来进行评价。第一种经济法,涉及到大量的经济数据需要单独统计和计算,而且很多经济数据统计和计算抽象不具体,比如零部件采购、物流、存储价格受市场行情等因素影响波动大;维修作业人员的工资、五险一金、福利等支出对应的人工成本难以与车辆挂钩核算。第二种基于车辆故障数进行评价,数据统计简单,可直接从车辆维修履历中调取,但笼统地将渐发性故障和突发性故障都进行了统计,因此对评价结果有影响,如正常使用过程中,需要定期更换的刹车片、雨刮胶条、火花塞等零部件。此外,以故障数作为评价依据,现有文献研究中虽然考虑了车辆的使用可靠性,但车辆故障类型未根据危害程度分类考虑。一次致命故障引起的危害和成本远远高于十次轻微故障引起的。
因此,基于以上研究成果,结合调研实际,通过建模,并结合车辆维修履历中维修故障数的统计与分析,进行维护周期优化效果评价,具有数据获取方便,操作简单等优点。为了客观地借助故障数进行科学地评价,对故障数进行统计时,既要区别渐发性故障和突发性故障,又要考虑不同故障类型对车辆的影响程度不同。因此在建模时引入当量系数[8]。
2 评价模型建立
维护周期通过合理优化,能提高车辆的运营效率,同时减少车辆的维护成本。若维护周期盲目地延长,可能会导致车辆的技术状况在下次维护周期到来之前已经恶化,从而导致车辆故障频发。以故障数和故障率等反映车辆可靠性的指标来评价周期优化效果,具有数据获取方便,操作简单等优点。
然而,故障按照发生的进程进行分类,可分为渐发性故障和突发性故障。为客观评价车辆维护周期优化效果,因车辆正常使用且需要定期更换的渐发性故障维修项目不在统计范畴。
此外,根据故障的危害程度不同,若将致命故障(一类故障)、严重故障(二类故障)和一般故障(三类故障)、轻微故障(四类故障)同等对待,也会影响评价效果的失真[9]。如在统计期内,维护周期优化后的车辆一类故障发生2 次,优化前车辆四类故障发生4次,不能说明优化效果好。因此,为综合考虑故障类型对车辆可靠性的影响,利用故障数和故障率更好地评价维护周期优化效果,在此引入当量故障率。
2.1 当量故障数
假设在统计期内,第i 辆车对应的一类故障数为r1i,二类故障数为r2i,三类故障数为r3i,四类故障数为r4i。
当量故障数的计算模型如下:

式中:εj为第j 类故障当量系数,j=1,2,3,4;rji为第i 辆试验车的第j 类故障数(统计期内),次。
针对当量系数的赋值,以三类故障当量系数为参照标准,可根据历史大数据分析,按照不同故障类型对应的故障维修时长、维修零部件成本等因素来单一或者综合比值。若没条件,可取ε1=100,ε2=20,ε3=1,ε4=0.2[8-9]。
在统计故障数时,需要指出的是:伴随着维护作业附加的突发性故障修理,也在本次统计范畴。
2.2 当量故障率
引入当量故障率是为了统计试验车辆单位行驶里程期间的当量故障数。
当量故障率的计算模型如下:

式中:Pi为第i 辆试验车(i=1、2、3…n)当量故障率(统计期内),次/103km;Lim为第i 辆试验车末次故障对应的仪表里程数(统计期内),103km;Lis为第i 辆试验车首次故障对应的仪表里程数(统计期内),103km;Ni为第i 辆试验车的当量故障数(统计期内),次。
2.3 平均当量故障率
引入平均当量故障率是为了统计所有试验车辆单位行驶里程期间当量故障数的平均数。
平均当量故障率的计算模型如下:

3 案例分析
西安市公共交通总公司先前将下辖所有营运公交车辆的二级维护周期里程从优化前的18 000±2 000 km,优化成了28 000±2 000 km。为验证优化效果,选取40 辆能代表西安市区路况的40 路混合动力公交客车为试验统计对象。剔除1 辆因交通事故导致的一类故障车辆和1 辆一起因产品质量问题导致的二类故障车辆,余下38 辆试验车,统计其维护周期优化前后统计期内的故障数据。具体统计数据如表1 所示。
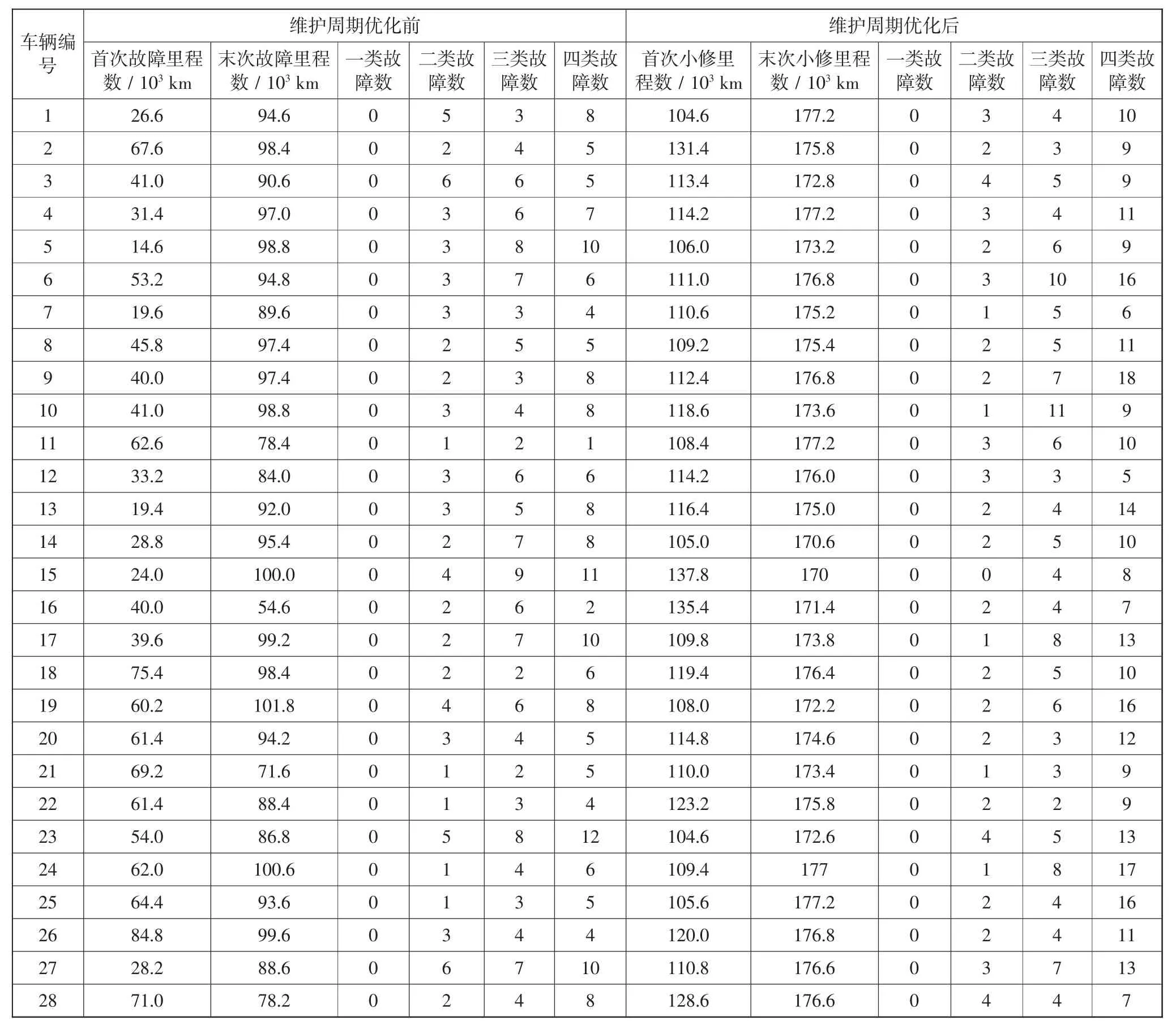
表1 维护周期优化前后统计期内车辆故障数
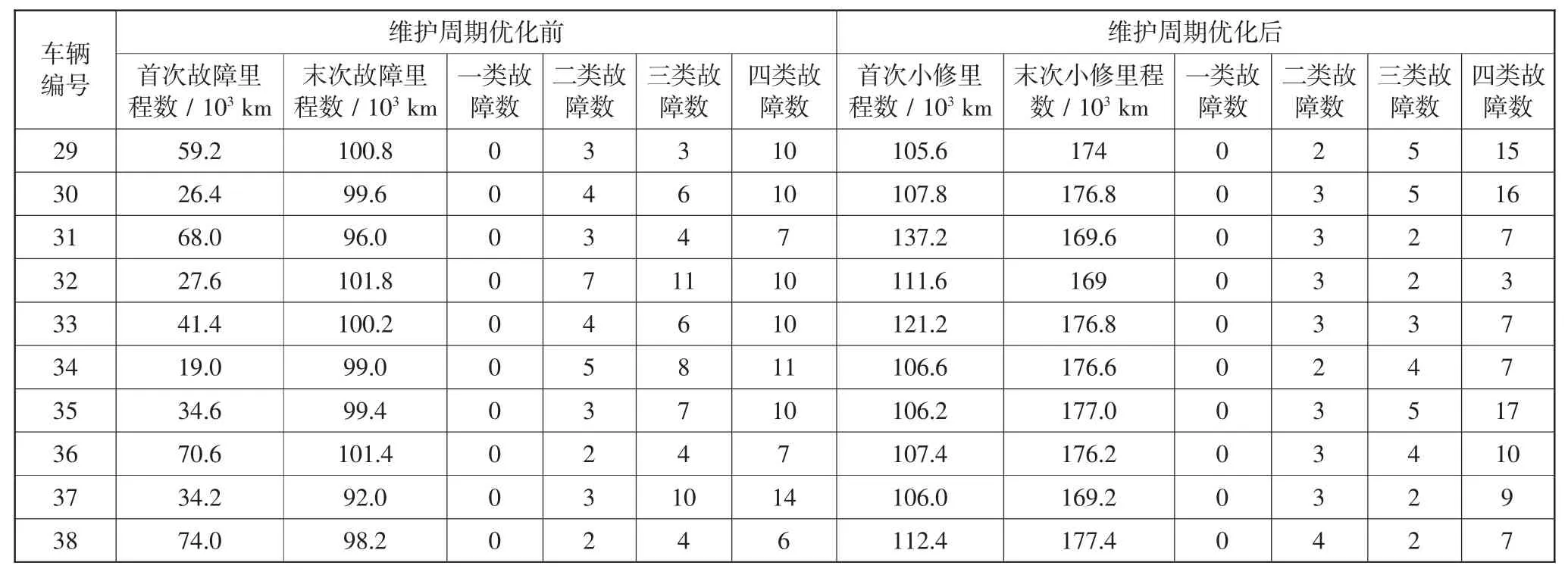
续表
当量系数,取值ε1=100,ε2=20,ε3=1,ε4=0.2。将表1 中统计数据代入公式(1)、(2)中,计算出每辆试验车辆的当量故障数和当量故障率,如表2所示。
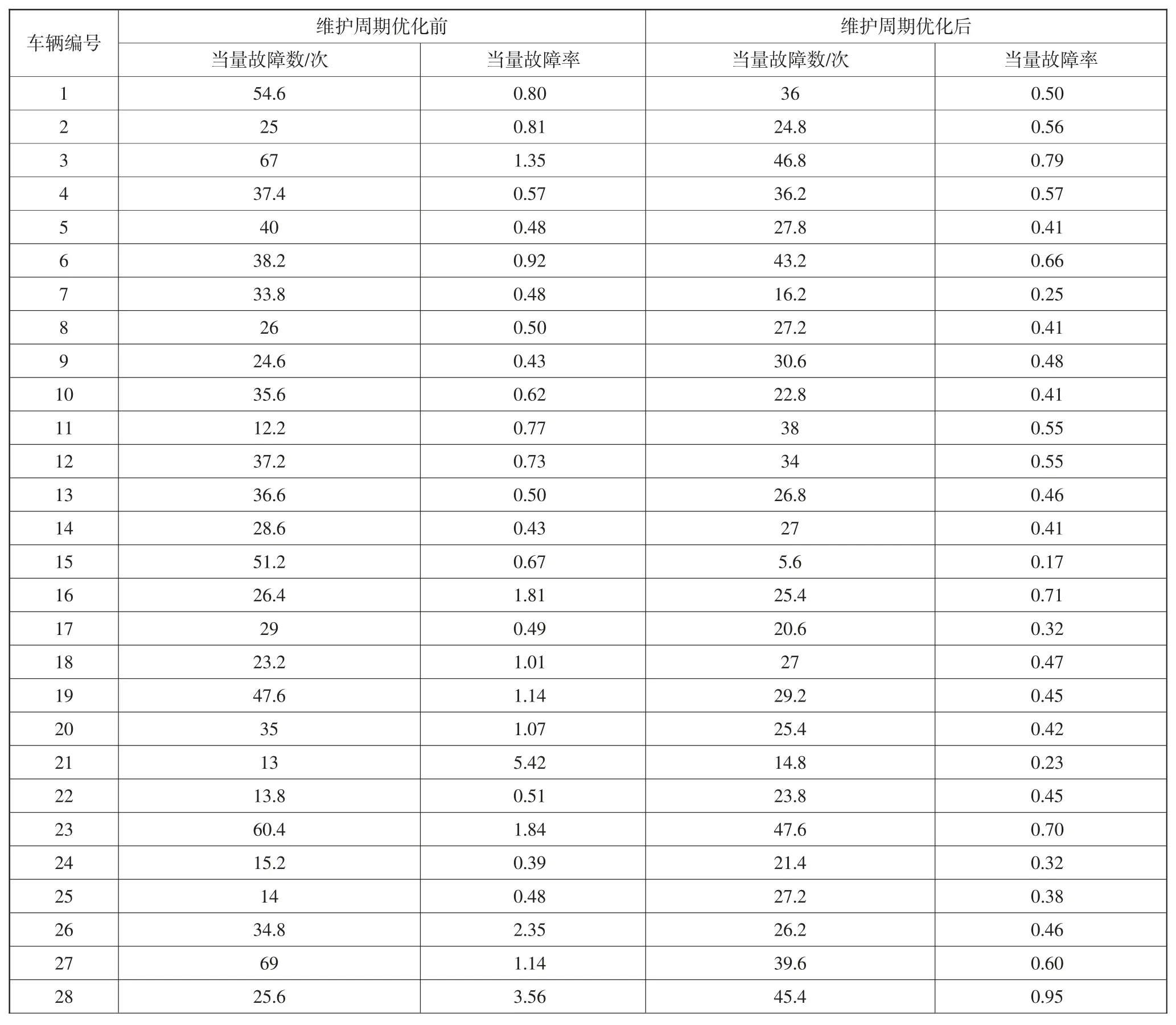
表2 维护周期优化前后车辆当量故障数与当量故障率统计分析表
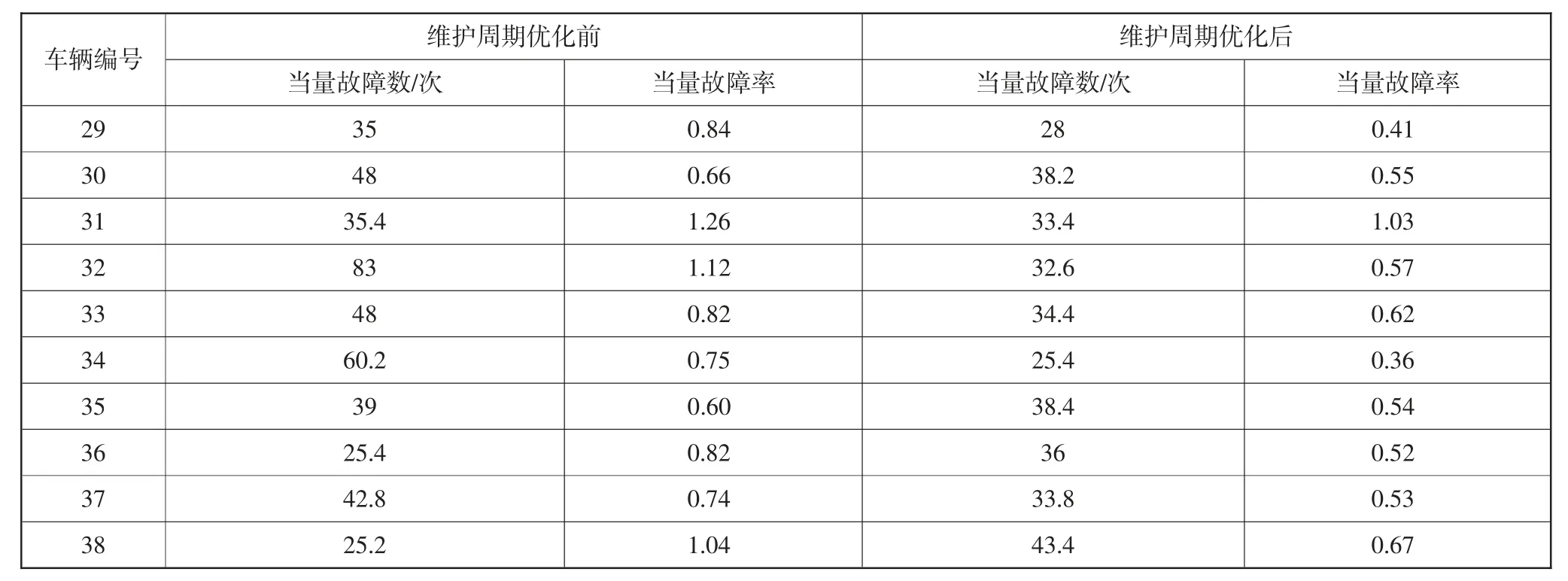
续表
将表2 中相关数据代入公式(3),计算优化前后的平均当量故障率:

二级维护周期优化前的试验车平均当量故障率(1.05 次/103km)高于优化后的(0.51 次/103km)。这说明二级维护周期优化后,单位行程的混动公交客车当量故障数下降了,车辆可靠性得到了有效的提升,进而说明维护周期优化效果较好。
4 结论
以容易获取的车辆维修履历中故障维修记录作为原始数据,将突发性故障及故障危害等级进行综合考虑,通过引入当量系数建模,进行数据统计和分析,最后通过比较维护周期优化前和优化后的平均当量故障率来评价维护周期优化效果。该评价方法具有数据获取方便,操作简单等优点。不足之处在于:
1)对故障数进行统计和分析时,需要剔除因车辆正常使用而发生的渐发性故障,并需要依据故障危害等级对故障进行分类。
2)为保证评价结果可靠,需要统计的试验车辆数及统计期要有一定的保障。
