微动并联机构柔性平板移动副求解

陈海真，王红梅，李爱军

(山东理工大学 机械工程学院, 山东 淄博 255049)

全柔性微动并联机构具有无间隙、无摩擦、响应快、误差积累小、定位精度高、结构紧凑等优点，近年来在生命科学、微机电系统(MEMS)、超精密加工等领域得到了广泛应用[1-3]。靠柔性关节的受力而产生的弹性变形来实现运动的传递是全柔性微动并联机构与传统并联机构的区别，它的关节柔度与运动性能和力的传递密切相关。关节柔度是一个多元函数，影响关节柔度的因素很多，如材料性能、关节轮廓曲线形状、关节尺寸、关节力等[4]。为了提高微动并联机构的设计精度，本文对柔性关节的柔度求解进行研究。

1 柔性平板移动副的柔度矩阵

柔性平板移动副常用的柔度计算公式[5]为

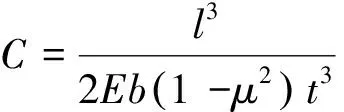
(1)

式中：b、l、t为移动副的结构尺寸；E为材料的拉伸弹性模量；μ为材料的泊松比。

式(1)虽然比较简洁，计算也比较方便，但是它给出的功能方向上柔度表达式存在较大的计算误差。为了适应现代科学，高精密微动机构的设计必须有相适应的计算方法，下面利用卡氏第二定理得出具有较高精度的柔性平板移动副柔度计算表达式。

1.1 柔性平板移动副力学计算模型

柔性平板移动副的受力简图如图1所示。图1中移动副左右对称，变形部分薄板长度为l、厚度为t，厚板长度为a、沿z方向即横向的宽度为b。中间CD段的厚度远大于两侧OC段和DB段的厚度，可视为刚体。移动副上所加外载分别是弯矩M、轴向力Fx、垂直力Fy，它们作用于移动副的A点。

图1 柔性平板移动副平面受力图

简化移动副受力，将移动副视为变截面三次超静定梁。因为在移动副的两端O、B处都各有3个约束力，为将原结构转变为基本静定系，先代之以相应的约束，除去O点原来的约束，基于原结构在原约束处位移相一致的协调条件，再利用卡氏第二定理[6]建立补充方程，最后结合静力平衡方程即可求得各约束力。

在工作平面内，柔性平板移动副的静力平衡方程为

(2)

移动副各段的轴向力、剪切力与弯矩分别为：

(3)

(4)

(5)

1.2 弹性变形应变能

平板移动副的应变能为弯曲应变能、轴向拉伸应变能、剪切应变能三部分[7]之和，即

(6)

式中：k为剪切影响系数，k=2.5；b为材料z方向的宽度；t为移动副的横截面积；μ为材料的泊松比。总应变能的表达式为

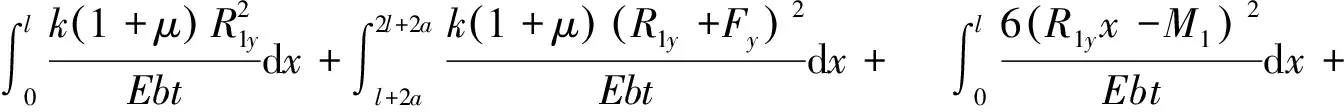
2(R1y+Fy)[Fy(l+a)+M1+M]f4+

[Fy(l+a)+M1+M]2l}

(7)

式中：

1.3 柔度矩阵求解

由卡氏第二定理可以求解柔度矩阵[8-10]。根据卡氏第二定理和O点的约束条件可得O点沿x、y、θ的位移分量分别为：

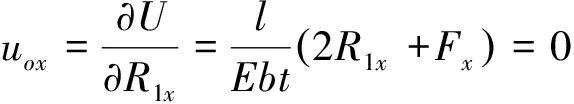
(8)

[Fy(l+a)+M1+M]f4=0

(9)

[Fy(l+a)+M1+M]l}=0

(10)

将式(8)、式(9)、式(10)联立,求出O点各个约束力

(11)

式中：

应用卡氏第二定理同样得A点各方向的位移分量：

(12)

[2Fy(l+a)+M1+M+R1y(l+a)]f4+

[Fy(l+a)+M1+M](l+a)l}

(13)

[Fy(l+a)+M1+M]l}

(14)

将式(11)代入式(12)～(14)即可得到柔性关节输出位移、所加载荷及柔度矩阵的表达式

(15)

2 柔度系数与结构参数的关系

柔度系数与平板移动副的结构参数、材料的泊松比μ、拉伸弹性模量E有关。确定了移动副的材料后，柔度系数的大小仅取决于平板的结构参数。利用MATLAB工具，可以得出各柔度系数与平板结构参数的关系。

平板移动副各段尺寸为：a=10 mm；宽度b的变化范围是8～12 mm；长度l=20 mm；变形部分薄板厚度t=1～3 mm；材料为弹簧钢65Mn，其泊松比μ=0.3；弹性模量E=190×103MPa；剪切影响系数k=2.5。在Fx作用下x方向的柔度系数为Cx-Fx，在Fy作用下y方向的柔度系数为Cy-Fy；M作用下，转角θ方向的柔度系数为Cθ-M。通过MATLAB程序计算得到各柔度系数与平板厚度t与宽度b的关系图，如图2所示。

在关节厚度t与宽度b的变化范围内，柔度系数Cθ-Fy与Cy-M的最大值分别为2.959 4×10-19rad/N和7.809 9×10-19mm/(N·mm)；最小值分别为-8.120 5×10-19rad/N和-1.474 9×10-19mm/(N·mm)，两个系数的值都非常小，因此可以将两个系数的值近似看作零。

取变形部分薄板长度l=15～25 mm；薄板厚度t=1.5 mm；中间刚体部分长度a=10～15 mm；横向宽度尺寸b=10 mm。各柔度系数与平板尺寸a、l的变化关系图如图3所示。

(a)柔度系数Cx-Fx随l、a的变化图 (b)柔度系数Cy-Fy随l、a的变化图 (c)柔度系数Cθ-M随l、a的变化图

在关节长度尺寸a与l的变化范围内，柔度系数Cθ-Fy和Cy-M的最大值分别为5.684 3×10-19rad/N和4.8945×10-19mm/(N·mm)；最小值分别为-5.6843×10-19rad/N和-4.8390×10-19mm/(N·mm)，与各柔度系数随平板厚度t和宽度b的变化情况相似，两系数的值都非常小，因此近似计算时可以忽略两个系数的影响。

由以上分析，可以得到下述结论：

(1)由图2可知，3个主要柔度系数的值，随着平板关节厚度t和宽度b的减小都是增大的。从图2(b)和图2(c)可知：当关节厚度t的值较大时，柔度系数Cy-Fy与Cθ-M几乎不受关节宽度b变化的影响。

(a)柔度系数Cx-Fx随b、t的变化图 (b)柔度系数Cy-Fy随b、t的变化图 (c)柔度系数Cθ-M随b、t的变化图

(2)从图3(a)和图3(b)可知，中间刚体部分尺寸a的变化对柔度系数Cx-Fx与Cy-Fy没有影响，但是两柔度系数都随长度l的增大而增大；由图3(c)可知：随l的增大和a的减小，柔度系数Cθ-M的值都是增大的。

因为柔度系数Cy-M与Cθ-Fy近似为零，忽略其对计算精度的影响，移动副的简化柔度矩阵为

(16)

柔性平板移动副沿y轴方向的输出位移uAy为功能位移，而沿x轴方向的位移uAx及绕z轴的角位移uAθ则是由外载引起的位移误差。为了减小误差，要求柔性移动副非功能方向上的位移尽可能小，而功能方向上的位移尽可能大。

3 柔性平板移动副的有限元模型

用ANSYS软件建立柔性平板移动副的有限元模型，并对其功能方向上的弹性变形进行静力学分析。材料与前面相同，弹性平板移动副的各段长度尺寸为a=10 mm；l=20 mm；宽度b=10 mm;变形薄板部分厚度t=1.5 mm；驱动载荷Fy=200 N。柔性平板移动副功能方向上的位移云图如图4所示。

图4 柔性平板移动副y方向的位移云图

在几组不同驱动力Fy作用下，柔性平板移动副功能方向位移及误差的计算结果与传统方法计算结果的对比见表1。

分析表1的计算数据和实验结果可以看出，本文提出的计算方法与传统的计算方法相比，计算结果的精度有了明显提高，误差稳定在1.235%左右。

表1 柔性平板移动副功能方向的位移及误差分析Tab.1 Displacement analysis and error analysis of function dimension for flexible parallel-plate prismatic pair

4 结束语

本文建立了柔性平板移动副力学简化计算模型，基于卡氏第二定理得到了柔性平板移动副在其工作平面内的柔度计算公式，并对各方向柔度系数随柔性移动副结构参数的变化规律进行了分析。应用ANSYS软件建立柔性平板移动副的有限元模型，并进行了仿真分析，通过对比分析传统方法计算数据、此方法理论计算数据及有限元分析数据可知，所得柔性平板移动副的柔度计算公式计算精度有了明显提高。本文提出柔性平板移动副的柔度计算方法，还给出了平面内非功能方向上的柔度系数，这为生命科学、超精密加工等领域中高精密微动机构的设计和精度分析提供了理论基础。