基于变分模态分解与模糊聚类的船用齿轮箱故障诊断

丁颖苗 上海市嘉定区航务管理所

鲍慧玲 上海开放大学嘉定分校

船用齿轮箱作为船舶动力装置中的核心组件之一，其运行可靠性和稳定性显得十分重要。然而，齿轮箱的工作环境相当恶劣，容易出现不同程度的损伤和故障。因此，对于船用齿轮箱采取有效、准确的故障诊断是非常有必要的。

故障诊断的核心内容大致由特征提取和模式识别两个部分构成。其中，特征提取是从杂乱无章的原始信号中提取出若干特征参数量，来表征和反映设备当前的运行状态；模式识别则是通过一些智能算法将具有相同或相似特征的样本归到一起，从而对设备故障类型做出识别。

齿轮箱振动信号具有非线性、非平稳特性，一般的信号分析方法应用效果不佳，甚至在信号分解时可能出现模态混叠、端点效应等问题，因而有必要加强特征提取的效果。变分模态分解方法实质上是一组自适应的维纳滤波器，具有扎实理论基础，能够较好地避免上述问题。根据已有研究发现，利用其滤波组特性，将此分解方法应用在提取时变振动信号等方面具有不错的效果。而若将VMD与多特征融合技术进行结合并应用于齿轮故障诊断中，则可为齿轮故障的及时预警提供相关参考。

模糊聚类作为原型聚类中经典的一种算法，对于样本分类问题具有不错的效果，在故障诊断领域中也是较为主流的模式识别方法。综上所述，本文将充分发挥VMD方法和KFCM算法各自的优势，采用VMD方法提取信号特征，以KFCM作为模式识别分类器，对二者进行结合应用于船用齿轮箱的故障诊断。

1.变分模态分解

模态分解方法是众多特征提取手段中的一种，传统的信号分解是基于极值点拟合包络原理或者在此基础上改进的，从而出现一些不可避免的缺陷。VMD方法是近几年由Konstantin Dragomiretskiy团队提出的信号分解方法，该方法另辟蹊径，将问题转化为求解约束变分方程的策略来解决，有着传统模态分解方法不可比拟的优势。

VMD方法的分解原理如下：

（1）预估信号分解为k个模态分量，随机初始化这些分量的中心频率ωk的值，然后对分解得到的各分量uk采取希尔伯特变换，可得变换后的解析信号为：

（2）对各个分量的频谱进行平移至各自基频带，以所有频带带宽之和最小作为目标，分配各分量的带宽，构造得到带约束的变分方程为：

（3）结合惩罚项系数α和拉格朗日乘子λ，将带约束的变分方程转化为无约束变分方程：

（4）采用乘子交替方向法求解上述方程，持续更新各分量，直至原始信号被分解为预估分量，蕴含着相关特征信息的中心频率也一同被提取出来。

2.核模糊聚类

聚类算法在模式识别分类领域的应用并不少见，而核模糊聚类则是其中经典的一类。该算法以聚类结构为基础，并假定可通过一组原型展开描述，对原型随机初始化，然后对其不断进行迭代更新，直至聚类结果不再发生变化，算法终止。求解过程中将各样本点与各均值向量的欧式距离尽可能达到最小作为目标，并且不断更新簇划分和均值向量，最终得到的稳定状态下的簇划分和均值向量。

KFCM聚类原理如下：

（1）令Φ(xj)表示将xj从原始空间映射到高维空间后的特征向量，则目标函数可表示为：

式中：uij为第j个样本对第i个簇的隶属度；m为权值；n为样本总个数；ƒ为聚类簇数；vi为均值向量。

（2）计算过程中，由于样本xi和样本xj映射到高维特征空间后的内积 不方便直接计算，因此引入核函数：

（3）容易得知，代入核函数之后的欧式距离为：

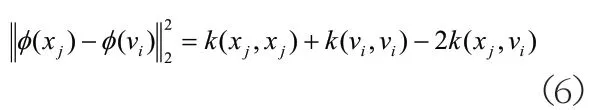
（4）利用拉格朗日乘子法寻优得到目标函数与隶属度分别可表示为：

其中，经典核函数主要有线性核、高斯核、多项式核、拉普拉斯核和Sigmoid核等。在此选取高斯核函数：

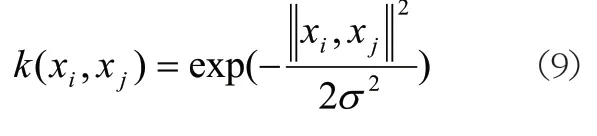
3.基于VMD与KFCM的船用齿轮箱故障诊断流程

图1 断齿时域信号

图2 断齿频域信号

图3 VMD分解后的各信号分量

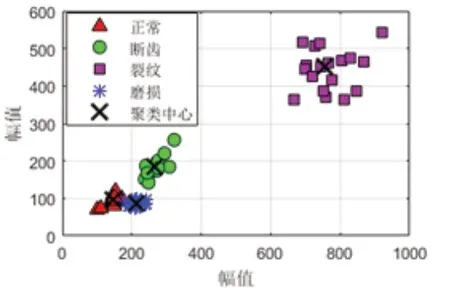
图4 聚类结果二维图

VMD分解过程中直接将各个模态在频域范围内不断更新求解，通过傅里叶逆变换到时域，并且将不同的模态按预定个数从低频至高频逐个分解出来。而KFCM聚类通过引入核函数的方法来对传统FCM聚类进行改进，从而增加了类与类之间的差异度，克服了经典FCM聚类对模糊类别不好处理的情况。本文集成两者优势，提出基于VMD与KFCM的齿轮箱故障诊断方法，具体诊断流程如下：

（1）在某工况下测得齿轮正常、断齿、裂纹和磨损等四种状况时的振动信号数据，分别对其作零均值处理。随机选取其中M组数据构造训练样本集，剩余N组构造测试样本集。

（2）采用V MD方法对四类齿轮信号展开分解。分解前对主要分解参数模态个数K与二次惩罚因子α择优，而后对分解得到的k个IMF分量整合，获得初始特征向量子矩阵。

（4）以相同的方法提取其余故障类型的特征向量，并将它们进行合并从而获得训练样本集。

（5）利用KFCM算法对训练样本集X进行训练，获得相应聚类模型，并通过该模型对测试样本集Y分类验证，评价模型分类性能。

4.试验分析

本文的数据来源于实验室环境下的齿轮箱故障综合模拟试验台，该试验台由交频电机、轴承支座、齿轮箱、磁粉制动器以及控制柜等构成。交频电机的额定转速设为1500r/min，载荷电流为0.1A，输入轴转频ƒz=1500/60=25HZ，啮合频率ƒn=1500＊55/60=1375HZ。

试验过程中对正常齿轮、轮齿断裂、齿轮磨损以及齿根裂纹等四种齿轮状态进行了模拟，并采集相应振动数据。其中，采样频率设为10240Hz，采样时间4s，可获得不同齿轮状态下40960个数据点。将这些数据点等长度截成20段，并且随机选取其中的18组用于训练，剩余2组用于测试。最终，构造得到大小为72＊2048的训练样本集和大小为8＊2048的测试样本集。以轮齿断裂故障为例，其相应时域信号和频域信号分别如图1、2所示。

表1 测试样本奇异值及聚类结果

变分模态分解在非线性非平稳信号的分解上确实有着巨大优势，但是其主要参数模态个数k和二次惩罚因子α的选择对分解结果具有一定的影响。根据相关实验研究表明，k值过大可能会出现虚假模态，过小又不能完全将原信号中的特征信息提取出来；α值过大可能会导致部分特征频率混叠，反之则会出现分解模态的边频带变宽从而使得特征频率模糊化。因此，以分解后的模态不发生混叠以及保证重构信号与原始信号具有一定的相似度作为目标，经多次试验综合评判选定k=5,α=10000作为VMD分解主要参数。此外，设置保真度系数τ与分解精度ε分别为0和1e-7。

在确定分解参数后，对断齿故障的振动信号进行VMD分解，得到一系列具有不同特征尺度的平稳信号。对于每个IMF分量，它们拥有各自的特征频率，也蕴含着相应的故障信息。分解后各分量的时域信号分布情况如图3所示。

将VMD分解后的5个IMF分量作为初始特征向量子矩阵，以同样的方法获取其余训练样本矩阵，然后对这些矩阵整合成大小为72×5的初始特征向量矩阵。

矩阵奇异值由于具有稳定性以及比例不变性等良好性质，常常作为矩阵的固有特征来应用。即使矩阵中的某些元素发生一定范围内波动，矩阵奇异值也不会发生较大波动。因此，将上述矩阵中的每个IMF分量作奇异值分解，得到相应奇异值矩阵来刻画和描述原始特征向量矩阵。

样本集分类类别设置为c=4，模糊加权指数m的取值范围是1.5～2.5，这里选取中间值2。算法中最大迭代更新次数设为100，隶属度最小变化量则设为1e-5。通过对72组训练样本集进行模糊聚类训练，获得分类矩阵U和聚类中心V。为使聚类效果更加形象直观，聚类结果以二维图的形式给出，如图4所示。观察可以发现，四个聚类中心相互间隔较远，同种故障类别聚集度高，不同故障类别间隙明显，说明经过训练后，四种齿轮状态聚类效果明显，故障分类效果良好。

将剩余的8组测试样本同样进行奇异值分解，再利用KFCM算法分类，以测试本文的故障诊断模型的效果，测试样本集分解后的奇异值与聚类结果如表1所示。其中，Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表齿轮正常、轮齿断裂、齿根裂纹和齿轮磨损四种齿轮状态。可以发现，相同齿轮状态下的奇异值向量特征近似一致，从聚类结果也可看到，所有状态类别的分类结果全部准确，说明训练后的诊断模型分类性能较好，通过实例论证了文中所提出的齿轮箱故障诊断方法是有效的。

5.结论

针对船用齿轮箱故障诊断精度不高的问题，本文提出了一种基于VMD与KFCM结合的故障诊断方法。引入VMD方法到齿轮箱故障诊断中，采用VMD分解后得到的IMF分量的奇异值来构造初始特征向量矩阵，再将该特征向量矩阵输入到KFCM分类模型中训练。通过对四种状态下的齿轮箱振动数据的训练和测试，结果表明，该方法的故障识别率较高，诊断效果较好。