炮孔近区岩体振动主频及能量的数值模拟
2020-09-15郑博闻刘飞香李新平张雪屏
罗 忆,郑博闻,2,刘飞香,李新平 ,张雪屏,2
(1.武汉理工大学道路桥梁与结构工程湖北省重点实验室,武汉430070;2.武汉理工大学土木工程与建筑学院,武汉430070;3.中国铁建重工集团股份有限公司,长沙 410100)
在国家“一带一路”的战略背景下,岩体爆破技术在水利、交通、矿山等行业的应用越来越广泛,由于岩体结构的特殊性以及爆破振动信号的复杂性、非平稳性,如何有效精准地预测和控制爆破振动对保留岩体所造成的破坏效应仍是当前研究的一大难题[1]。
单一利用爆破振动速度来控制岩体稳定性存在一些问题,现行爆破振动安全规程[2]综合考虑振动速度和振动频率来监测和控制岩体稳定性,而在爆破振动速度研究方面现有研究成果较多,所以近些年爆破振动频率逐渐成为研究的热点问题。夏祥等[3]模拟得出了质点振动主频的衰减规律,以及振动主频与炸药药量之间的关系。卢文波等[4]发现爆破地震波幅频分布曲线存在多峰结构,爆破振动的主频并不是随着爆心距的增大严格递减,而是会在局部出现跳跃现象。周俊汝等[5]结合实测资料发现爆破振动平均频率随爆心距的增大规则地衰减。杨润强等[6]发现随着地应力的增加,爆破振动的主频会减小,低频振动成分会增加。李洪涛等[7-8]对比研究了地下洞室梯段爆破与露天梯段爆破等不同类型爆源形式下爆破地震能量的分布特征。
单孔爆破作为最简单最基础的情况,一直是学者们研究的重点,而研究侧重点主要在于不耦合系数,徐颖等[9]发现不耦合系数为1.67时的爆破裂纹长度最长,并且不耦合系数的增加会导致裂纹数目减少。王志亮等[10]发现当不耦合系数在3.0以内时,孔壁压力、加速度、速度的下降速率较快,而大于3.0时衰减速率很小。王伟等[11]发现合理的不耦合系数,可使岩石不形成粉碎区,并且能量耗散大幅度减少。姜鹏飞等[12]发现当不耦合系数大于2.0时,不耦合系数对岩石应力及峰值速度影响不明显。钟明寿等[13]发现当不耦合系数为1.5时,采集的地震波信号主频低、信噪比最高。梁为民等[14]发现耦合装药条件下粉碎区更大,而不耦合装药条件下形成的裂纹更稀疏、更长。王夏南[15]发现径向不耦合系数在1.15~1.5内时,波峰波谷处的应力强度最强。
相对于爆破中远区,爆破近区振动响应更加复杂,傅洪贤等[16]通过现场实测对萨道夫斯基公式进行了完善和补充。胡英国等[17]利用数值模拟手段,得出了爆破近区岩体临界损伤峰值质点速度。谢烽等[18]得出适用于近区振动预测模型,随着离爆源距离的增加,振速的衰减速率逐渐变小。
在爆破振动频率方面的研究相对较少,特别是针对爆破近区方面研究更少,需要尽快揭秘爆破近区岩体爆破振动频率传播和衰减特性。笔者从最简单的单孔爆破模型入手,采用ANSYS/LS-DYNA模拟研究了爆破近区的振动响应,通过改变不耦合系数,研究不耦合系数与爆破振动主频以及能量之间的变化规律。
1 理论分析
1.1 振动主频
在振动频率衰减机理研究方面,国内学者[19-20]参照萨道夫斯基公式,通过量纲分析得到爆破振动主频预测公式:
(1)
(2)
式中:f为爆破振动主频预测值;Q为装药量;R为爆心距;PPV为质点峰值振动速度;K、α为与介质特性、爆破方式、传播途径有关的系数。
另有学者[21-22]推得的主频预测公式分别为
(3)
(4)
式中:f为爆破振动主频预测值;a1、a2为待定常数;Q为装药量;R为爆心距;Cs为岩体横波波速,cm/s;kf为频率系数,kf=0.01~0.03。
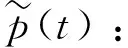
(5)
式中:f为频率;i为虚数单位。
爆炸荷载的频谱可以表示为
(6)
文献[23]根据三角形爆炸荷载推得爆炸荷载的幅值谱为
(7)
式中:pmax为爆炸荷载形成的峰值压力;tr为爆炸荷载达到峰值所需的上升时间;td为爆炸荷载全历程持续时间。
径向不耦合装药时,爆炸峰值荷载p0为
(8)
式中:ρ0为炸药的装药密度;D为爆轰波沿炮孔方向的传播速度;γ为等熵指数,对于一般的岩石炸药起爆,取γ=3.0;a为炮孔的装药直径;b为炮孔直径。
1.2 振动能量
爆炸过程中,爆生气体在炮孔中膨胀压缩间隙中的空气产生冲击波,而后又冲击炮孔壁,可认为爆生气体膨胀充满整个炮孔。在该过程中,爆生气体的体积增大,密度减小并且音速也降低,从而导致其波阻抗发生变化。
文献[24-25]认为爆生气体膨胀充满整个炮孔过程视为等熵绝热膨胀,其密度和音速分别为
(9)
(10)

(11)
将式(9)和式(11)代入式(10)中,得
(12)
传递给岩石的能量可表示为
(13)
由式(12)可知,岩体中爆炸能量的传递与炸药和岩石的波阻抗、装药不耦合系数有关。
用|F(ω)|2表示爆破振动信号中不同频率成分所对应的功率谱密度,将其定义为功率谱函数,功率谱密度PSD表示了一定频率对应谐波分量的能量的相对大小。
爆破发生时,对于空间中质量为Δm的质元在t时刻的动能可以表示为:
(14)
式中:E(t)为爆破振动在t时刻的振动能量;v(t)为质元在t时刻的振动速度。
对质元质量进行归一化处理,在振动时程t1→t2内对质元振动速度进行积分,得到爆破振动信号的总能量Eq:
(15)
式中:Eq为爆破振动的总能量;t1,t2分别为爆破振动信号记录的起止时刻。
由于爆破振动采集到的是一系列离散值,所以上式可以表示为
(16)
式中:v(ti)为离散的爆破振动速度采样序列;Δt为采样时间间隔。
2 单孔爆破数值模拟
2.1 数值模型
采用ANSYS/LS-DYNA有限元动力分析软件,建立了爆破二维平面有限元模型。模型长10 m、宽10 m,在模型四周设置无反射边界,模型左侧施加位移约束,炮孔位于模型左下角(见图1),炸药直径32 mm,采用不耦合装药,不耦合系数K分别取1.3、2、2.5、3、3.5五种不同工况对比分析,在模型对角线上间隔1 m依次选取10个测点。

图1 有限元数值模型Fig.1 Finite element numerical model
在模拟计算中,采用流固耦合的计算方法,用ALE算法将炸药、空气、岩体三者相耦合,采用JWL状态方程[26]描述爆炸过程,其状态方程表达式如下:
(17)
式中:V为爆生气体相对体积;A、B、R1、R2、ω、E均为状态方程材料参数。
JWL状态方程对应参数如表1所示,其中:A、B、R1、R2、ω为与炸药相关的材料参数;E0为初始内能比,V0为初始相对体积[27]。

表1 炸药和JWL状态方程参数
空气介质模型状态方程采用Gruneisen方程描述,具体材料参数如表2所示。
(γ0+αμ)E2
(18)
式中:ρ2为空气材料密度;γ0为Gruneisen参数;C为曲线截距;α为γ0的一阶体积修正;S1、S2、S3均为曲线斜率的系数;μ为体积修正量。

表2 空气材料参数
岩体采用随动强化本构模型,结合河南南阳天池抽水蓄能电站现场岩体参数,具体岩石参数如表3所示。

表3 岩石参数
2.2 爆心距与主频及能量的变化规律
根据文献[3]的研究,质点振动速度的主频按下式定义:
(19)
式中:F1,F2分别为水平直线y=Fmax/2与速度频谱曲线交点横坐标的最小值和最大值;Fmax为傅里叶频谱曲线上的极大值。
模拟计算爆心距1 m处的振速频谱极大值Fmax为4 600 Hz,取Fmax/2为2 300 Hz,与频谱图得到的交点F1,F2分别为3 560、8 850 Hz,进而求得爆心距1 m处的振动主频为6 205 Hz(见图2)。
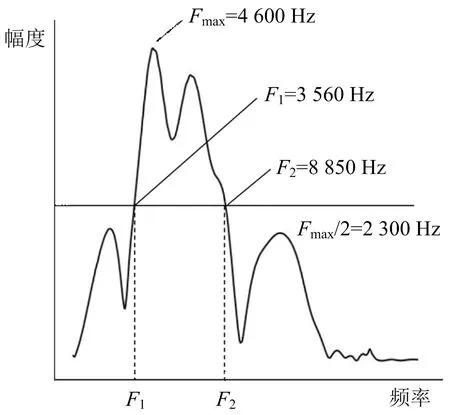
图2 爆心距1 m处振动主频Fig.2 Dominant frequency of vibration at 1 m from blast center
不同爆心距的振动速度频谱如图3所示。对比爆心距分别为2、3、4 m处的振速频谱发现,振速频谱图在2、3、4 m处分别呈现5峰、6峰、7峰(极大值点)的结构,可见随着爆心距的增加振速频谱的峰数目是逐渐增大的,即频率由某个区段集中分布逐渐变为多个区段均匀分布的形态。对比爆心距1、5、10 m三处测点,在1 m处振速频谱呈现4峰结构,频率主要集中在4 000~10 000 Hz,但在5、10 m处频谱呈现多峰结构,频率主要集中在3 000~8 000 Hz。

图3 不同爆心距的测点频谱Fig.3 Frequency spectrum of measuring point at different distance from blast center
根据式(19),求出在不耦合系数K=1.3的工况下,爆心距1~10 m范围内爆破振动速度主频,K=1.3代表工程中常用的炮孔直径42 mm,药卷直径32 mm的工况。为了便于分析主频的衰减规律,选取10 m处的最小主频作为基准,将主频归一化整理,得出主频衰减变化规律(见图4),主频在2 m处最大,3 m处主频迅速衰减变小,3~6 m主频基本保持稳定,在6 m处还有小幅度增大,但在6 m之后主频又迅速直线衰减,说明了爆破振动速度主频并不是随着爆心距的增大而严格递减的。
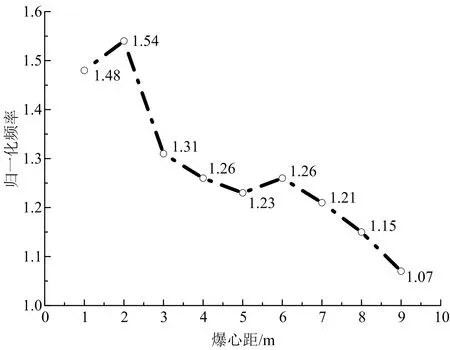
图4 主频衰减Fig.4 Dominant frequency attenuation
爆破振动速度时程曲线经傅里叶变换,获得离散化的频率值系列和对应的功率谱密度PSDi系列。分别对不同频率段的功率谱进行积分,得出在一定频带范围内的能量分布情况[28]。频率范围(fm,fn)内的爆破振动能量占总能量的比例:
(20)
式中:PEi为频率范围(fm,fn)内的爆破振动能量占比。
将0~15 000 Hz按照2 500 Hz为界限划分为6个区段,选取爆心距分别为1、5、10 m处测点的能量占比分析(见图5),在爆心距1 m处5 000~7 500 Hz段的占比最多,达到了29.7%,但与其他频段占比相差不大,总体呈现正态分布。在爆心距5 m处,占比在2 500~5 000 Hz和5 000~7 500 Hz较大,两个频段相差不大,仅相差1.8%,并且能量主要集中在2 500~10 000 Hz这个范围内,约占总能量的80%以上,对比1 m处,该占比约仅有70%,说明随着爆心距的增大,频带能量逐渐往主频靠拢。在10 m处,能量最大占比则在2 500~5 000 Hz频段,并且达到了37.9%,进一步说明了随着爆心距的增大,能量往主频段附近集中,能量分布由高频均匀分布变为低频集中分布。
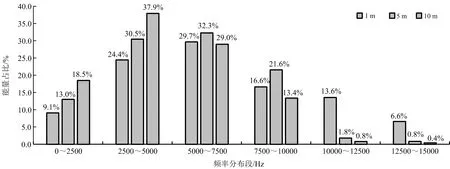
图5 各频率段能量占比Fig.5 Energy ratio of each frequency segment
爆心距1、5、10 m处的峰值振速、主频、总能量如表4所示,从1 m增至5 m处峰值振速和总能量分别衰减了73.0%和71.7%,5 m到10 m处则分别衰减了50.9%和43.1%,可见随着爆心距的增大,峰值速度和能量迅速减小并且衰减速率是逐渐变小的。但从1 m到5 m处,振动主频衰减了17.0%,5 m处到10 m处则衰减了18.8%,可见振动主频的衰减速率是基本稳定的,与峰值振速和能量的衰减速率有所不同。

表4 速度、主频、能量衰减对比
2.3 不耦合系数与主频及能量的变化规律
选取最小主频作为基准值,将主频归一化处理,同样选取不同不耦合系数下1、5、10 m处的振动主频(见图6),随着不耦合系数的增大,振动主频总体上呈现先增大后减小再增大的趋势。当K<2时,振动主频随K的增大而增大;当2
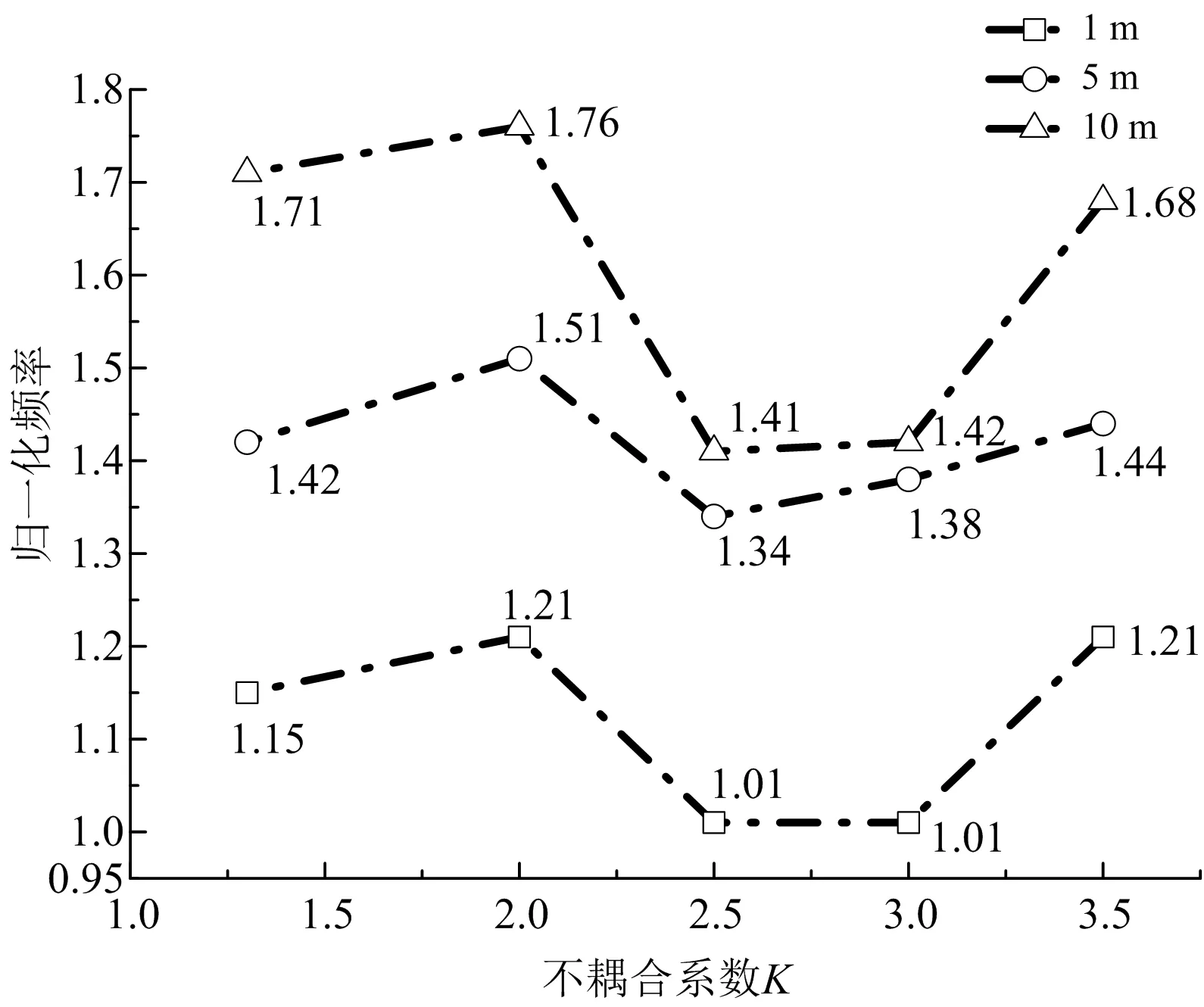
图6 主频随不耦合系数变化规律Fig.6 Variation of dominant frequency with decouple ratio
同样将能量归一化处理(见图7)得出,能量随着不耦合系数的增大先增大后减小,变化规律与峰值速度相同,当不耦合系数K=2.5时,在爆心距1、5、10 m处能量均达到了最大值,并且在1 m处能量的增减幅度更大。说明不耦合系数的改变对离炮孔较近处能量的变化影响更加明显。
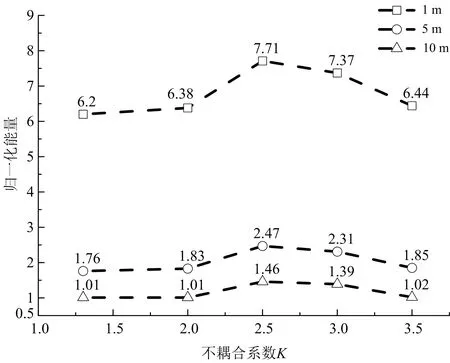
图7 能量随不耦合系数变化规律Fig.7 Variation law of energy with decouple ratio
各频率段能量占比如表5所示,主频所在的2 500~5 000 Hz和5 000~7 500 Hz两个区段,爆心距1 m测点,随着不耦合系数的增大主频先增大后减小再增大,同样主频所在5 000~7 500 Hz区段能量也呈现相同的变化趋势,与2 500~5 000 Hz占比的差值同样先从5%增大到15%后减小至10%再增大到15%。在5 m测点,K=1.3时两段能量占比相差不大,随着不耦合系数的增大到2时,5 000~7 500 Hz段能量占比要多15%,但当K增大到2.5、3时,两段能量占比又相差不大,当K=3.5时,两段能量占比又拉大到15%左右,总体与主频一样呈现先增大后减小再增大的变化趋势。在10 m测点,主频位于2 500~5 000 Hz区段,K=1.3时,2 500~5 000 Hz区段能量占比比5 000~7 500 Hz多9%,不耦合系数增大到2.0时,5 000~7 500 Hz段能量占比比2 500~5 000 Hz段多约20%,发现不同于1、5 m测点,两段的能量占比差距变得更大,总体规律与主频变化规律一致,进一步说明了主频与能量之间的密切关系。
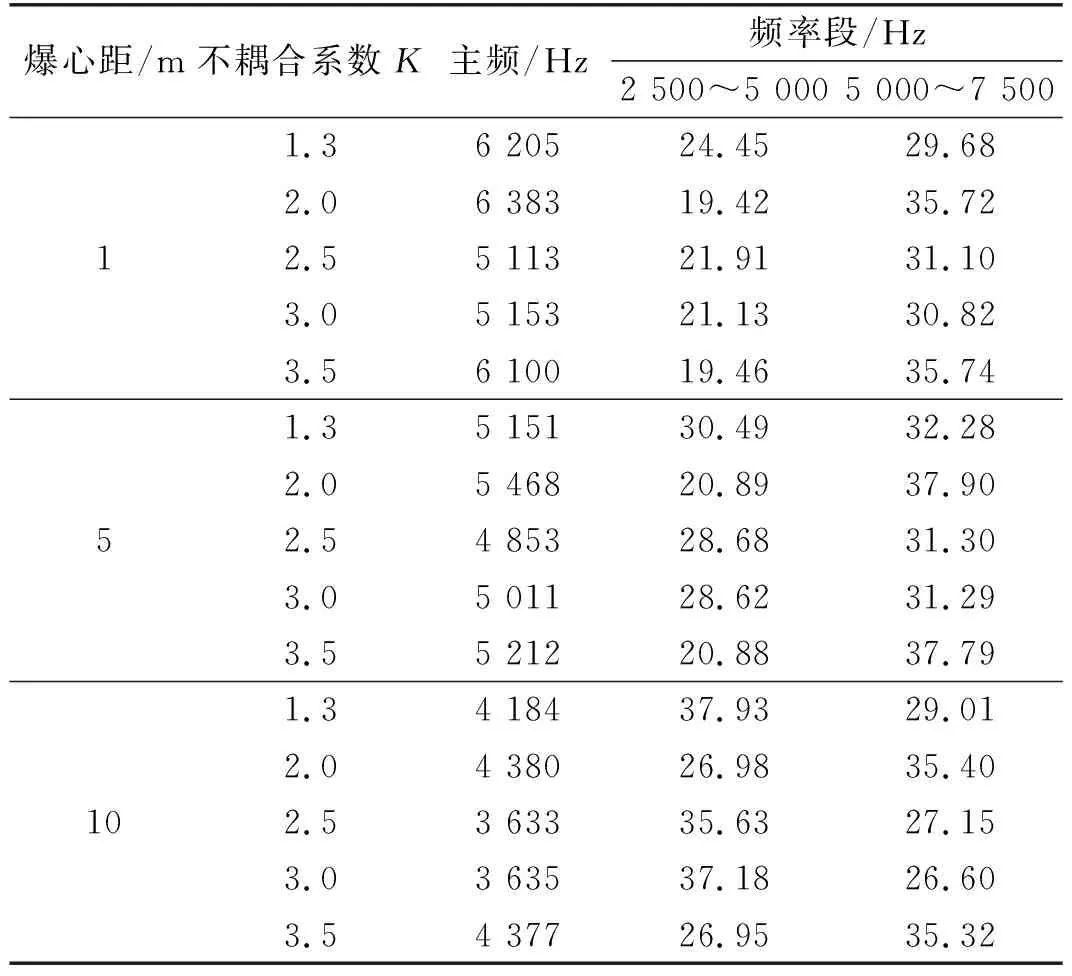
表5 各频率段能量占比
3 结论
1)在爆心距10 m范围内,随着爆心距的增大,爆破振动主频在爆心距2 m处达到峰值,随后迅速衰减,在3~6 m范围内保持稳定,6 m之后再次迅速衰减。
2)在同一爆心距位置,随着不耦合系数的增大,振动主频呈现先增大后减小再增大的趋势,而能量呈现先增大后减小的趋势。当不耦合系数为2.5时,爆破振动主频最小,爆破振动能量最大。
3)爆破振动能量在距离炮孔较近处在各个频率段均匀分布,但在炮孔较远处各频段能量逐渐由分散变为相对集中,并且向主频所在的频率段集中。
本研究数值模拟计算基于各项同性假设,为了排除其他因素干扰和提高计算效率,没有考虑岩体中的节理、裂隙等结构面的影响,在该方面还需要进一步的研究完善。所得研究结论将为后续多孔爆破研究提供理论依据和参考。
