转子泵流量脉动系数的通用模型研究
2020-09-15
(宿迁学院,江苏宿迁 223800)
0 引言
转子泵是一类基于转子与泵体间相对运动的容积泵,应用广泛[1-4]。旋转过程中,伴随着共轭位置的瞬间变化,瞬时流量也发生周期性的脉动,导致输出流量和工作不稳定,尤其对精密液压传动系统更为不利[5]。同时,流量脉动所引发的压力脉动,也会使管道,阀等元件产生振动和噪声[6]。对此,国、内外展开了大量的单泵级脉动计算[1-6]、设计与仿真[7-8]、试验等[9];以及系统级流量脉动[10-11]及热影响[12]等研究。截至目前,研究所针对的主要为已知型线的各类转子泵,所建立的脉动指标——流量脉动系数模型的针对性强,通用性差;一个能适用于各类转子泵的通用模型,却未见相关文献报道。因此,拟就该模型的通用性和简洁性作进一步深入研究。
1 面积法求解瞬时流量
本文以圆弧转子泵为例,其轴向截面如图1所示。其中,o1,o2为主、从转子中心,主、从转子的形状尺寸完全一致;o1k1、o2k2为主、从转子的顶圆半径;n为共轭运动点;转子宽度为b;主、从转子的旋转为逆、顺时针方向;由此所围成区域o1no2k2k1的容积为V。

图1 瞬时流量扫过面积的求解方法
设在dt的微小时间内,主、从转子的旋转角度为dθ;o1no2k2k1的容积变化为dV。由瞬时流量的定义得:
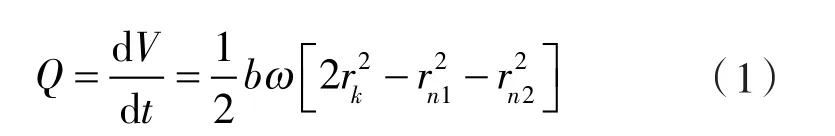
式中 Q ——瞬时流量;
rn1,rn2——主、从转子在n点处的半径;
ω ——旋转角速度;
rk——顶圆半径。
2 脉动系数的通用模型
流量的脉动因数定义为:
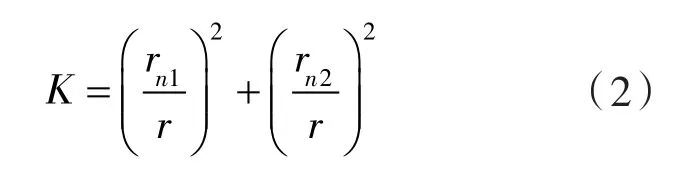
式中 K ——流量的脉动因数;
r ——节圆半径。
由转子泵流量公式可求得转子宽度b为:
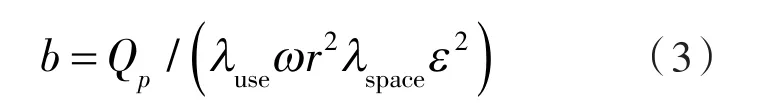
式中 Qp——转子泵流量;
λspace—— 转子泵的容积利用系数;
λuse——λspace的可利用系数,取λuse=0.85;
ε ——转子形状系数。
容积利用系数为[13]:
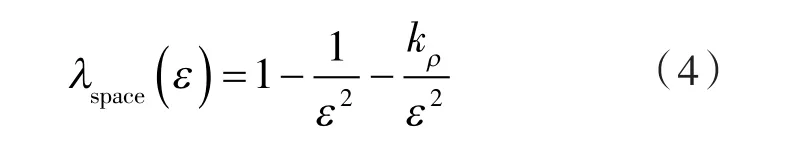
式中 kρ——工作轮廓的类型系数。
当工作轮廓为渐开线段时,kρ为:

由流量脉动系数的定义,得其通用模型为:
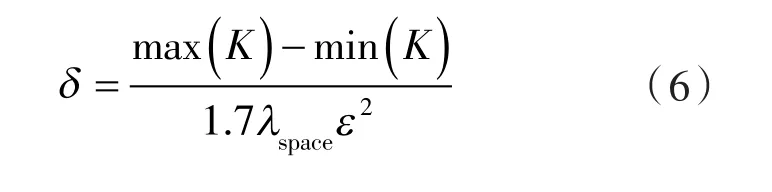
3 型线方程和脉动因数
转子型线由节圆(即瞬心圆)之内的谷型线和之外的峰型线的两部分组成,如图2所示。

图2 转子型线坐标方程的通用求解方法
以o1为原点,峰部对称轴线(简称峰轴)为y轴,构建xo1y坐标系。其中,记主转子型线上的运动点为n1,与之对应的共轭点为n2;n1,n2对应的节圆瞬心为 p1,p2,则 n1的瞬心半径ρ=p1n1;pk,pv为 p1,p2的起始位置,则 n1的法向角α =∠pkp1n1;θ=∠pko1p1为p1在节圆上的对应滚角;φ=0.5π/N为型线角,N为转子叶数,则峰型线角∠pko1p和谷型线角∠pvo1p均为0.5 φ。当峰型线上的运动点n1由起始位置向节点p移动,即其瞬心p1由pk以θ∈[0,0.5 φ]滚向节点p时;谷型线上的共轭点n2则也由其起始位置向节点p共轭移动,其瞬心 p2同样由 pv以θ∈[0,0.5 φ]滚向节点 p。
设n1在xo1y坐标系中的坐标为(x1,y1)。则峰型线的通用方程为:
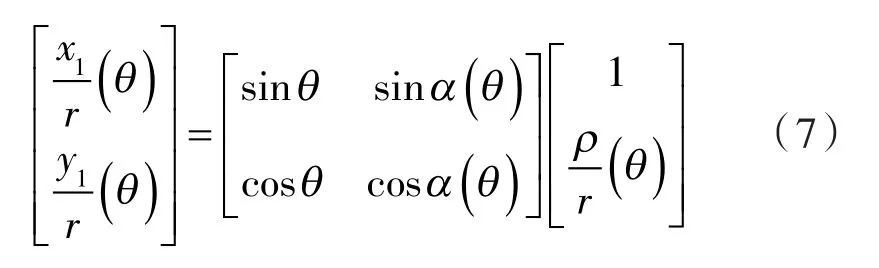
设 n2在 xo1y坐标系中的坐标为(x2,y2)。由n1和n2间的共轭关系,得谷型线的通用方程为:
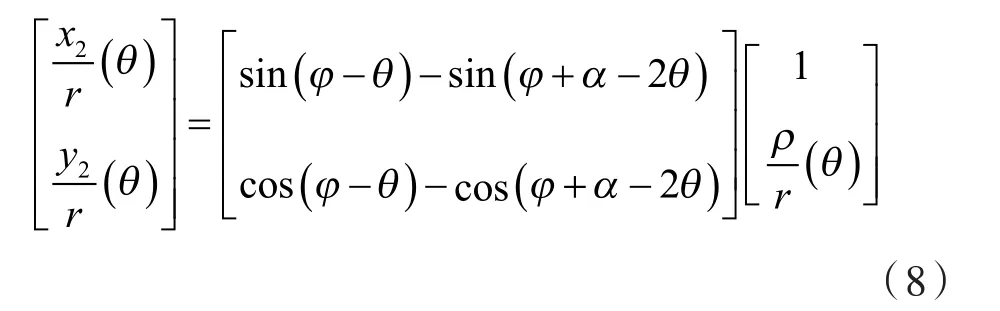
任意类型转子的型线通用模型,重点在于共轭型线的确定,而其它辅助型线则相对比较简单。故,共轭型线的通用方程能代表转子型线的通用性[14-18]。
将式(7)、(8)代入式(6),得:

4 瞬心半径及其法向角
在泵转子型线的构成方面,存在着单一峰型线和组合峰型线的2种情况。其中,单一峰、谷型线的起始位置位于峰轴、谷轴上,例圆弧转子[14-15]、摆线转子[16]和直谷型转子[17];而组合型线中的共轭型线段的起始位置不位于峰轴、谷轴上,例渐开线转子[18],下面将就这些常见转子型线,直接给出其瞬心半径和法向角的公式。
由文献[14-15]的进一步推导,得圆弧转子型线为:
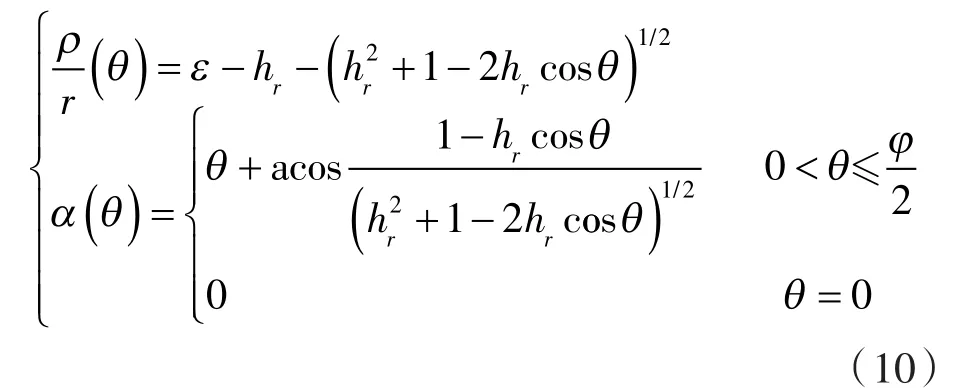
式中 hr—— 圆弧型线的圆心到转子中心的距离与节圆半径的无量纲比值。

其中,ε(N)的取值上限εmax(N)为:
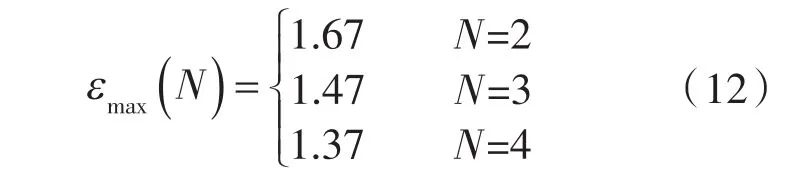
由文献[13]的进一步推导,得摆线转子型线为:
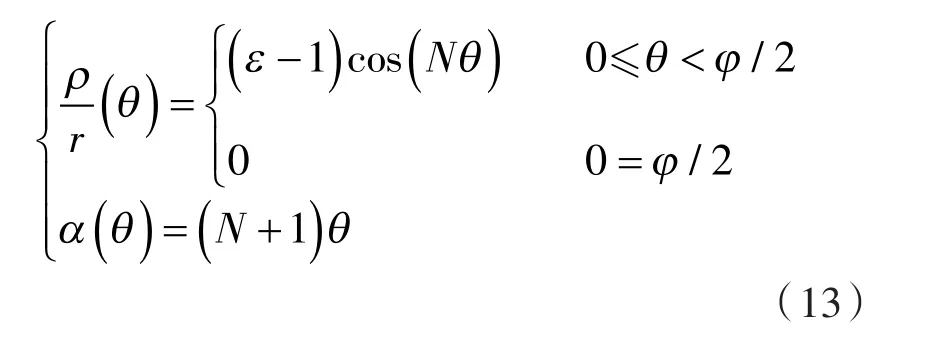
其中,ε(N)为定值,ε(N ) ≡1+ 1/N 。
由文献[14]的进一步推导,得直谷转子型线为:
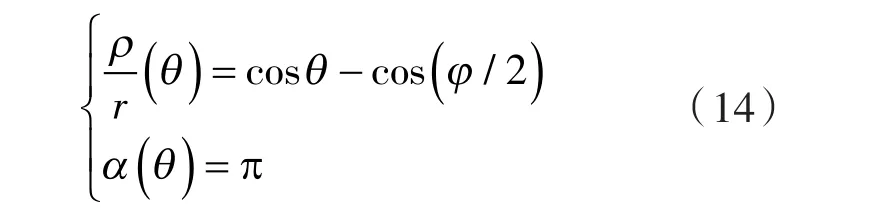
由文献[15]的进一步推导,得渐开线转子型线为:

其中,ε(N)的取值上限 εmax(N)为:
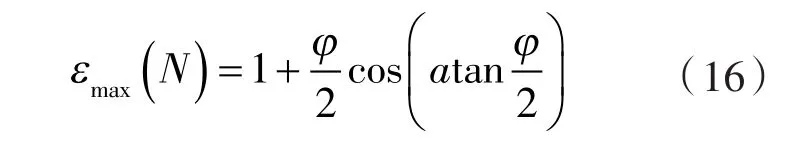
由式(10)~(16)可知,叶数和型线类型由上限(例圆弧、渐开线型)或定值(例摆线、直谷型)直接决定了形状系数的取值。
5 实例运算及结果分析
圆弧和渐开线既是最为常见的2种转子,也代表了单一和组合的2种型线类型,故下面仅就这2种转子,作进一步的实例运算及结果分析。
令:

则,渐开线转子的K—t特性曲线如图3所示。

图3 不同叶数和形状系数下的动态脉动因数
图3中,圆弧转子和渐开线转子的最大脉动因数max(K)、最小脉动因数min(K)均发生在t=0、t=1的型线端点上,其中,max(K)发生在t=0的起点上,min(K)≡2发生在t=1的终点上;且N↑→ε↓→max(K)↓。
以形状系数ε=1.36为例的max(K)—N变化情况,如表1所示。其中,由max[K(N,圆弧)]≡max[K(N,渐开线)]≡2.259,知转子叶数和型线类型对max(K)无影响。即max(K)可由单一型线类型下的最大脉动因数来统一定义。则,由单一型线类型的:
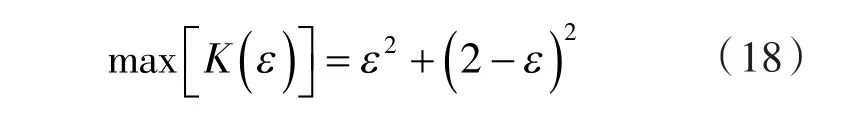
得式(6)的进一步简化式为:
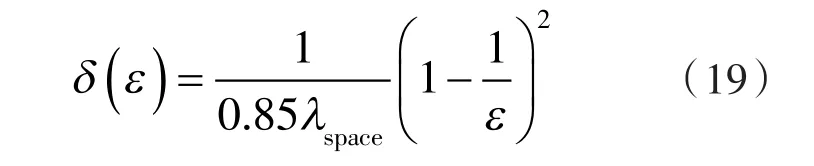
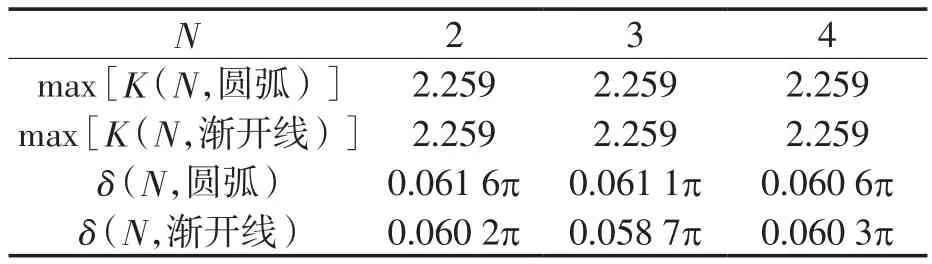
表1 ε=1.36、N不同下的最大脉动因数和脉动系数
表1中,由δ(N,圆弧)≈δ(N,渐开线),知N、型线类型对δ(N)因λspac的差别而有少许的影响;同时也说明在同形状系数的情况下,N、型线类型对λspace的影响甚微。
6 结论
(1)叶数和型线类型由上限(例圆弧、渐开线型)或定值(例摆线、直谷型)直接控制了形状系数的取值。
(2)最大脉动因数发生在共轭型线段的起点上,最小脉动因数≡2发生在位于节圆的终点上;同形状系数不同叶数和型线类型下的最大脉动因数相同。
(3)同形状系数下的叶数和型线类型对容积利用系数的影响甚微,从而对流量脉动系数的影响不大。
(4)形状系数为影响流量脉动系数的直接要素,形状系数越小,流量脉动系数越小。
