多陷阱复杂环境下机器人导航路径蚁群规划方法

王明超

（无锡工艺职业技术学院，江苏 宜兴 214200）

1 引言

移动机器人的导航路径关乎机器人自身安全、使用寿命和生产效率，导航路径要求短而光滑，光滑路径可以减少机器人磨损、提高行走效率[1]，因此研究机器人导航路径规划问题具有明显的经济意义。

机器人导航路径规划问题分为两大部分内容，即环境建模与路径规划策略。环境建模法有栅格法、可视图空间法、自由空间法、虚拟力场法等，可视图优点是线路清晰明确，容易规划出最优路径，缺点是普适性差，且只能应用于全局路径规划[2]；自由空间法是可视图空间法的改进方法，适用性较好，但是在复杂环境下算法复杂度极高[3]；虚拟力场法优点是复杂度低，缺点是空间中障碍物分布复杂时很可能求不到最优解；栅格法优点是简单、容易理解、普适性极好，缺点是障碍物“膨化”方法会损失部分工作空间[4]。路径规划策略分为传统方法和智能算法两类，传统方法有人工势场法、模糊逻辑法等，人工势场法原理简单、路径光滑性，缺点是容易陷入局部最优，甚至在目标点附近徘徊[5]；模糊逻辑法优点是不需要精确的系统模型，但是模糊逻辑表较难制定[6]；智能算法包括遗传算法、神经网络、蚁群算法等[7，8]，智能算法优势是发挥算法智能性，规划路径较优，但是问题也明显，算法本身都存在一定缺陷，如遗传算法运算效率低，神经网络算法需要一定量的训练样本，蚁群算法收敛速度慢、易陷局部最优等。

研究了多障碍物复杂环境下的导航路径规划问题，将陷阱深度标记策略和分种群搜索策略融入到蚁群算法中，提出了多种群蚁群算法。在多障碍物复杂环境中，多种群蚁群算法规划的路径长度和迭代次数明显优于基本蚁群算法。

2 机器人导航路径规划问题描述

2.1 环境建模

栅格法是环境建模最为简单有效的方法，虽然在障碍物“膨化”处理时会损失部分工作空间，但是却极大地降低了计算复杂度。

在机器人的二维工作空间中，使用固定大小的栅格划分工作区域，当障碍物未充满栅格时，使用“膨化”方法使其占满栅格。某区域的栅格模型，如图1所示。图中黑色栅格表示障碍物栅格，白色栅格表示不含有障碍物的自由栅格。为了区分障碍物栅格与自由栅格，为其赋不同的属性值，其中障碍物栅格赋值为1，自由栅格赋值为0，这样就可以将栅格模型转化为机器人可以识别的（0～1）矩阵模型。

图1 栅格建模法Fig.1 Grid Modeling Method

栅格的编码方法有顺序编码法和坐标法两种，路径表示时使用编码法，距离计算时使用坐标法，因此必须明确两者的转换关系，为：

式中：i—栅格顺序编码号；N—栅格规模；（xi，yi）—栅格坐标；mod—求余运算；fix—取整运算。

在此需要强调的是，在栅格环境下，机器人路径表示为一系列数据序列的集合｛a1，a2，…ai，…｝，使用蚁群算法在栅格环境下求解导航路径时，规划路径的栅格数是不固定的，无需限定数据序列的维数。

2.2 建立路径评价函数

在大多数路径规划问题中，一般以路径长度作为评价路径优劣的唯一标准，但是当路径中转弯较多、转弯较急时，会对机器人造成转弯磨损而影响使用效率，且转弯的存在也会影响行走效率，所以路径平滑度极大地影响机器人使用寿命和工作效率，因此将平滑度作为路径的一个评价指标。

（1）路径长度Lk的计算。路径长度为相邻栅格距离的累加和，即：

式中：a—路径中的栅格数；D（i，i+1）—第i个栅格与第i+1个栅格的距离。在栅格环境下，D（i，i+1）只能取值为1或。

（2）路径平滑度Sk的计算。使用路径转弯时的拐角大小表征路径平滑度，转弯时拐角大小定义方法，如图2中α所示。

图2 拐角大小定义方法Fig.2 Definition Method of the Corner

3 蚁群算法及分析

3.1 蚁群算法原理

以旅行商问题为背景对蚁群算法进行分析，记需访问的城市数量为n，蚁群中蚂蚁数量为m，城市i与城市j间距离为dij，两城市间在t时刻的信息素为τ（ijt），则蚂蚁k在t时刻由当前城市i转移到城市j的概率

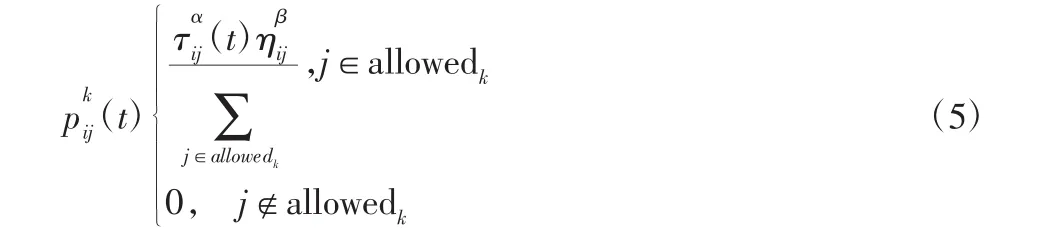
式中：ηij—启发信息，表示蚂蚁由城市i转移到城市j的期望程度；α、β—信息素和启发信息影响因子，代表信息素和启发因子在路径引导中的影响力，其值越大代表信息素或启发因子影响力越大，路径搜索收敛性越强，同时越容易陷入局部极值，其值越小代表路径规划随机性越大，越不容易收敛，但是容易跳出局部极值；allowedk—蚂蚁k可以选择的城市集合，即allowedk=n-tabuk，tabuk表示蚂蚁k的禁忌表，即蚂蚁k已经历的城市。

蚂蚁在行走过程中，边行走边释放信息素，这种信息素更新方式更符合蚁群实际。信息素更新方法为：

3.2 蚁群算法应用于栅格环境需明确的几点问题

蚁群算法最早基于旅行商问题提出，鉴于栅格环境下路径规划问题与旅行商问题的区别，明确以下几点：

（1）蚁群算法应用于栅格环境下路径规划时，allowedw表示蚂蚁k可以选择的栅格集合，即与当前栅格相邻的自由栅格除去禁忌表tabuk中的栅格；

4 多陷阱复杂环境下改进蚁群算法

蚁群算法存在收敛速度慢、易陷入局部最优的问题，且在多陷阱环境下这两个问题更加突出，提出了两种改进策略。

4.1 陷阱深度标记策略

在栅格环境下，最典型的陷阱为U型陷阱。在多陷阱复杂环境中，存在一定数量的蚂蚁陷入陷阱，目前解决陷阱问题存在蚂蚁回退策略和蚂蚁夭折策略两种方法。蚂蚁回退策略[9]为当蚂蚁陷入陷阱底部时，蚂蚁边倒退边标记陷阱栅格，直至回到离开陷阱，标记的目的是避免后续蚂蚁再次陷入陷阱。这种方法能够保证蚂蚁离开陷阱而完成路径规划，但是当环境中存在较多陷阱或陷阱较深时，大量蚂蚁经过反复的后退、标记、判断，会消耗大量的运算时间，而已经到达目标的蚂蚁需等待这部分未到达目标的蚂蚁，如此严重消耗了运算时间，降低了算法效率。

蚂蚁夭折策略[10]为当蚂蚁由起始点搜索至目标点时，路径搜索完成，蚂蚁正常死亡。当蚂蚁陷入U型陷阱时蚂蚁夭折，不再进行路径搜索，走过的路径不再进行信息素更新。但是当环境中存在较多陷阱时，会出现一定量的蚂蚁夭折，降低算法在解空间中的探索深度和解的质量。

在多陷阱复杂环境中，针对现有方法存在的问题，提出了陷阱深度标记策略。分以下两个步骤执行：

（1）陷阱的确认与深度计算。当蚂蚁k第一次出现可选栅格只有一个时，标记蚂蚁k当前栅格的前一栅格为Trap，且开始计数用于计算陷阱深度。当可选栅格只有一个连续出现且最终无栅格可选时，说明蚂蚁k陷入了U型陷阱，陷阱深度记为H；

（2）蚂蚁跳跃逃出陷阱。设置一个陷阱深度阈值HT，若H＆gt;HT说明陷阱较深，在陷阱中浪费时间较多，此时蚂蚁夭折，以免拖慢算法效率；若H≤HT说明陷阱较浅，在陷阱中浪费时间较少，此蚂蚁还可以继续使用，此时蚂蚁以跳跃方式直接跳跃至栅格Trap，同时将陷阱栅格标记为1，视为障碍物栅格，以免后续蚂蚁重蹈覆辙。

分析陷阱深度标记策略可知，以蚂蚁跳跃方式逃出陷阱，避免了回退策略中反复的回退、判断，节省了大量的运算时间，提高了算法效率。另外，当蚂蚁陷入U型陷阱时，没有像夭折策略一样直接扼杀，而是将陷入不深的蚂蚁进行了保留，与蚂蚁夭折策略相比保留了种群规模，提高了解的质量。

4.2 分种群搜索策略

式中：d（i，j）—栅格 i与栅格 j的距离；d（j，Goal）—下一栅格与目标栅格距离；k1、k2—近邻启发因子和目标启发因子的影响因子，分别表征算法的随机性和目的性。

对于第一个种群group1，设置k1＆gt;＆gt;k2＆gt;0，k1＆gt;＆gt;k2保证了算法初期具有足够的随机性，使蚂蚁拥有足够的自由充分探索解空间，避免算法在初期由于启发作用过于明显而陷入局部最优；k2＆gt;0而不允许取为0，保证了算法具有一定的启发引导作用，避免算法因完全的随机而严重偏离目标方向。对于第二个种群group2，设置k2＆gt;＆gt;k1且k1=0，这种设置方式使第二种群对路径规划具有较好的引导作用，提高算法收敛速度，且避免算法陷入极差解。

4.3 分种群蚁群算法流程

将陷阱深度标记策略与分种群搜索策略融入到蚁群算法中，得到分种群蚁群算法步骤为：

（1）参数初始化，包括种群数量m1和m2，信息素影响因子α、启发信息影响因子β、挥发系数ρ、陷阱深度阈值HT、近邻启发因子影响因子k1、目标启发因子影响因子k2、算法最大迭代次数N等；

（2）将两个种群的蚁群全部放置在起始点，蚂蚁按照式（5）和式（7）计算选择临近栅格的概率，而后使用轮盘赌的方法确定下一栅格；当可选栅格只有一个时，启动陷阱深度标记策略；所有蚂蚁边行走边进行信息素更新；

（3）当除夭折外的所有蚂蚁均到达目标点时，计算所有蚂蚁搜寻路径的长度并比较，输出算法本次循环的最优路径；

（4）判断算法循环次数是否达大于N，若否则算法转至（2）；若是则算法结束，同时输出最优路径。

5 实例验证

为了验证分种群蚁群算法在多陷阱复杂环境中路径规划的有效性，使用MATLAB软件分别仿真出多U型障碍物环境和多障碍物两种复杂环境，使用蚁群算法与多种群蚁群算法分别进行路径规划，对比路径优劣。

参数设置为：种群数量m1=25、m2=5，信息素影响因子α=1、启发信息影响因子β=6、挥发系数ρ=0.3、陷阱深度阈值HT=4、算法最大迭代次数N=50。

5.1 多U型障碍物复杂环境

仿真出20×20的U型障碍物密集分布环境，如图3所示。环境中U型障碍物多且深，栅格环境中1号栅格为起始点，标记为S，400号栅格为目标点，标记为G。基本蚁群算法使用蚂蚁回退策略应对U型障碍物环境，多种群蚁群算法使用陷阱深度标记策略应对U型障碍物，两种算法各运行100次，两算法规划的最优路径结果，如图3所示。图中虚线为基本蚁群算法规划的最优路径，实线为多种群蚁群算法规划的路径。

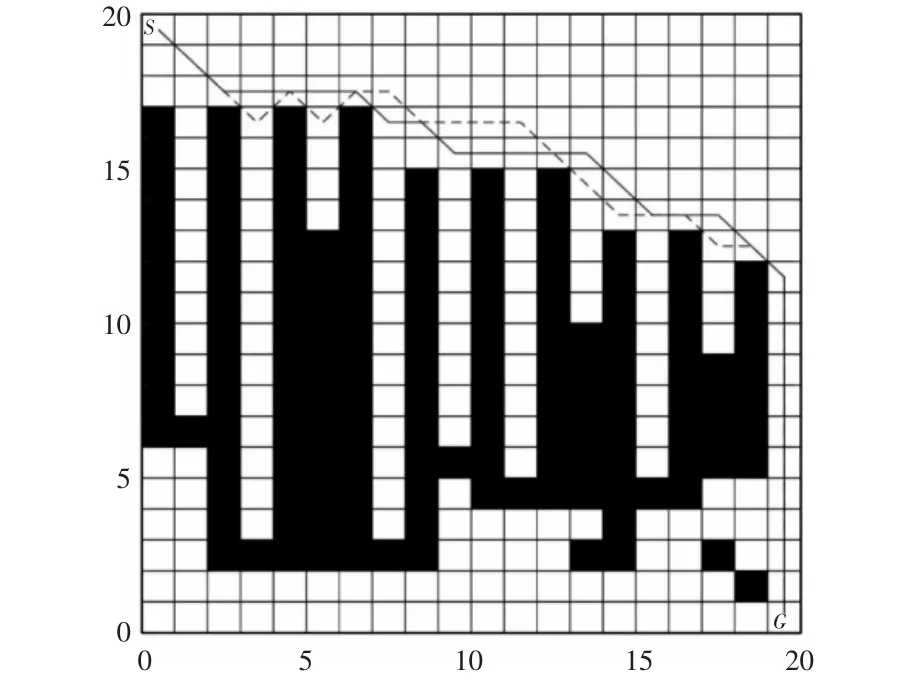
图3 多U型障碍物环境Fig.3 Multiple U-Shaped Obstacle Environment

统计两种算法的最优路径长度、算法平均运行时间与平均迭代次数结果，如表1所示。

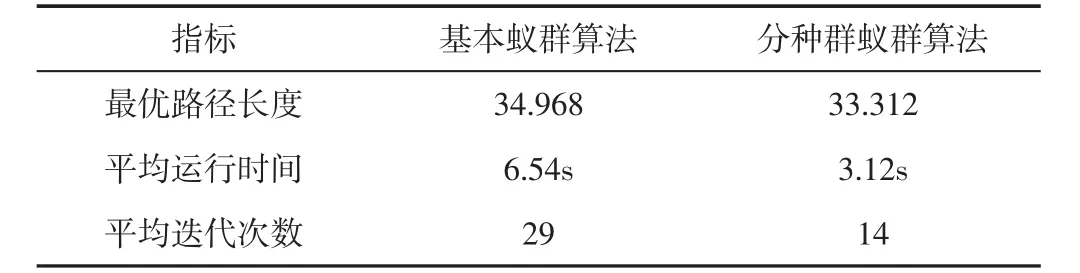
表1 两蚁群算法的运行结果Tab.1 Computational Result of the Two Ant Colony Algorithm

由表3可以看出，基本蚁群算法在多U型障碍物环境中规划出的路径折线特别多，这是因为蚂蚁后退到陷阱第一个栅格时不再后退而继续规划路径，导致规划出的路径非常不合理；而基本蚁群算法在陷入陷阱时会将前一栅格标记为，待确认陷入陷阱时以跳跃的方式直接回到栅格，使路径不存在折线。

由表1中数据可知，多种群蚁群算法规划的最优路径长度短于基本蚁群算法，且平均运行时间与平均迭代次数不足基本蚁群算法的一半，这是因为基本蚁群算法陷入U型陷阱时，蚂蚁反复的回退、判断严重拖慢了算法运行时间、增加算法迭代次数；而多种群蚁群算法在确认陷入U型陷阱时，直接跳跃至栅格，没有反复的回退与判断过程，极大地节省了运算时间、减少了迭代次数。

5.2 多障碍物复杂环境

仿真出20×20的多障碍物复杂环境，如图4所示。栅格环境中1号栅格为起始点，标记为S，400号栅格为目标点，标记为G。分别使用基本蚁群算法与多种群蚁群算法各进行100次路径规划，两算法规划的最优路径结果，如图5所示。虚线为基本蚁群算法规划的最优路径，实线为多种群蚁群算法规划的路径。算法迭代过程中，最优路径长度随迭代次数的变化情况，如图5所示。

图4 多障碍物环境Fig.4 Multiple Obstacles Environment

图5 最优路径长度随迭代次数变化曲线Fig.5 Changing Curve of Optimal Path Length with Iteration Time

由图4可以看出，多种群蚁群算法规划出的路径明显短于基本蚁群算法规划出的路径，多种群算法规划路径拐点数为5个，而基本算法规划路径拐点数为17个，说明多种群算法规划路径的平滑性明显优于基本蚁群算法。由图5可以看出，基本蚁群算法搜索到最优路径时迭代了26次，而多种群算法搜索到最优路径时迭代了13次。为了进一步比较多种群蚁群算法与基本蚁群算法在多障碍物环境中的路径规划性能，统计两算法的路径规划结果，如表2所示。

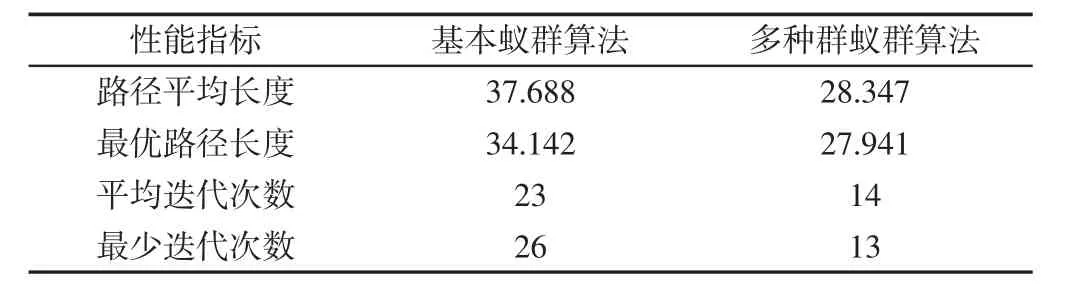
表2 两蚁群算法的路径规划结果Tab.2 Path Planning Result of the Two Ant Colony Algorithm

分析表2中数据可知，与基本蚁群算法相比，多种群蚁群算法规划路径的平均长度减少了24.8%，最优路径长度减少了18.2%，平均迭代次数减少了约39.1%，最少迭代次数减少了50%，以上数据充分说明多种群蚁群算法不仅规划路径短于基本蚁群算法，而且迭代次数也明显减少。这是因为多种群蚁群算法将蚁群分为两个种群，分别设置不同的启发信息，使蚂蚁搜索路径时具有不同的倾向性，兼顾了算法的随机性、目的性和收敛性，达到了提高算法收敛速度和寻优精度的目的。

6 结论

建立了多陷阱复杂环境下的栅格模型，提出了多种群蚁群算法用于路径规划，经仿真验证可以得出以下结论：（1）在多U型陷阱环境下，陷阱深度标记策略规划的最优路径比蚂蚁回退策略减少了4.7%，平均运行时间和平均迭代次数减少了一倍以上，说明了陷阱深度标记策略的规划效率和结果远远优于蚂蚁回退策略；（2）在多障碍物复杂环境下，与基本蚁群算法相比，多种群蚁群算法规划的路径平均长度减少了24.8%，平均迭代次数减少了近一倍，说明多种群算法中每个种群使用不同的启发信息，可以兼顾算法的随机性、目的性和收敛性，提高算法收敛速度和寻优精度。