基于模糊控制的双泵合流液压系统流量脉动特性仿真
2020-09-15陈贵全熊瑞平刘悦沆
陈贵全,熊瑞平,王 波,刘悦沆,彭 博
(四川大学机械工程学院,四川成都 610065)
引言
外啮合齿轮泵结构简单、工作可靠、制造容易、抗污染能力强,自吸性能好且价格低廉,因此在工程机械中得到了非常广泛的应用。其工作原理是利用一对齿轮的啮合运动,造成吸、排油腔的容积变化而进行工作。齿轮泵工作时,每个瞬间的流量不相同,存在着一定的脉动性,流量脉动是引起液压系统振动、噪声以及压力脉动的直接原因,如何减小液压系统中因为齿轮泵工作引起的流量脉动成为齿轮泵发展的一个重要方向[1]。
关于如何减小齿轮泵的流量脉动,文献[2]对齿轮有、无卸荷槽设计对泵的流量特性的影响进行了分析,证明了卸荷槽在齿轮泵中能够明显减小流量脉动。文献[3]提出了基于流量脉动系数进行齿轮泵齿廓设计,设计出的齿轮泵流量脉动系数比普通渐开线齿轮泵减少了22%。 文献[4]推导出具有不同齿数的主、从动齿轮的外啮合齿轮泵的理论流量脉动公式,指出采用多齿数的主动齿轮和少齿数的从动齿轮啮合传动的齿轮泵流量脉动明显降低。文献[5]基于MATLAB对渐开线外啮合斜齿轮泵的流量脉动特性进行了仿真分析,得出了在主要参数相同的情况下,斜齿轮的流量脉动远小于普通齿轮泵。文献[6]对外啮合异齿数斜齿轮泵流量脉动和流量特性进行了研究,得出了对于不同齿数的斜齿轮泵,流量脉动随螺旋角的增加而增加,随齿轮齿数的增加而减小,与齿轮模数无关。文献[7]采用Fluent 3D动态网格技术,对相同齿轮参数的双圆弧螺旋齿轮泵和普通无孔螺旋齿轮泵的流量脉动进行了比较和模拟,得出了双圆弧螺旋齿轮泵比普通无孔螺旋齿轮泵的流量脉动小得多。文献[8]推导出了齿轮泵的瞬时流量的计算公式,从理论上提出了采用2对齿轮错位叠加的方法可以有效减小流量脉动。文献[9]对液压系统双泵合流技术进行了探究,指出双泵合流后系统的流量脉动系数变为原来的23.85%,泵合流可以有效改善液压系统的流量脉动,但未考虑加入控制算法进一步改善系统流量脉动。
本研究利用AMESim搭建了双泵合流液压系统的模型,通过仿真探究了双泵合流对系统流量脉动的改善情况,同时通过AMESim-Simulink的联合仿真研究验证了利用模糊控制器根据系统的流量脉动特性调整两齿轮泵的转速,可以进一步改善了液压系统的流量脉动。
1 理论推导
1.1 外啮合齿轮泵瞬时流量
基于前人推导的外啮合齿轮泵瞬时流量的计算公式[10],得到瞬时流量的表达式为:
(1)
式中,n1—— 主动轮的转速
B—— 齿轮的厚度
R1—— 主动轮节圆半径
R2—— 从动轮节圆半径
h1—— 主动轮齿顶高
h2—— 从动轮齿顶高
f—— 啮合点与节点的距离
如果主从动轮是一对设计参数相同的渐开线齿轮,则有R1=R2=R,h1=h2=h,由齿轮结构的几何关系有:
h=Re-R
(2)
式中,Re—— 齿顶圆半径
R—— 节圆半径
根据渐开线的性质有:
f=Rjφ
(3)
式中,Rj—— 基圆半径
φ—— 齿轮泵转角
由式(1)~式(3)可得,当外啮合齿轮泵主从动轮设计参数相同时,其瞬时流量表达式为:
(4)
由式(4)可知,泵的瞬时流量随齿轮转角按抛物线规律变化。
齿轮在转动时,啮合点与节点的距离f会周期性不断变化。由式(3)、式(4)可知f值周期性变化会导致瞬时流量qv值的周期性变化。
在一对齿的完整啮合过程中,当啮合点和节点重合时,f=0,由式(3)可求得对应齿轮转角φ=0。由式(4)可知,此时瞬时流量最大;当一对齿刚开始啮合或啮合结束时,f=±0.5tj(tj为齿轮基节)[11]:
tj=2πRj/z
(5)
式中,z为齿轮泵齿数。
由式(3)和式(5)可求得对应齿轮转角φ=±π/z。由式(4)可知,此时瞬时流量最小。
由此可得到齿轮泵在一对齿的完成啮合过程中,瞬时流量随转角的变化如图1所示。

图1 一对齿啮合过程中的齿轮泵瞬时流量图
1.2 流量脉动系数
外啮合齿轮泵的瞬时流量在其平均流量附近脉动。为了评价瞬时流量的脉动,引入流量脉动系数δq,定义流量脉动系数[12]:
(6)
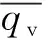
2 双泵合流液压系统流量脉动特性仿真
2.1 AMESim仿真模型
利用AMESim搭建的双泵合流液压系统仿真模型如图2所示。外啮合齿轮泵2,4分别由电机1和电机3驱动,溢流阀5用于限制系统的最大压力,起安全保护的作用,电磁换向阀6用于控制是否采用双泵合流的工作方式,电磁换向阀7用于控制卸荷回路的通断,节流阀8用于调节液压系统流量,流量计9用于测量系统流量。
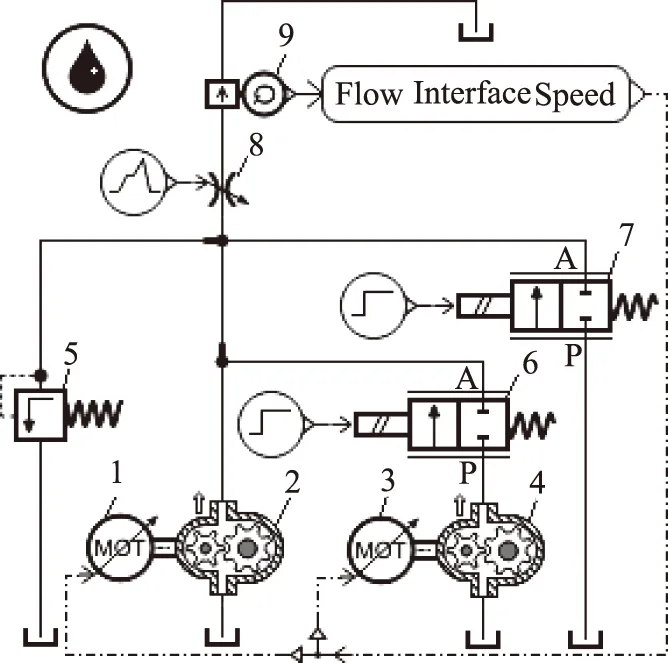
1、3.电机 2、4.外啮合齿轮泵 5.溢流阀6、7.二位二通电磁换向阀 8.节流阀 9.流量计图2 双泵合流液压系统原理图
2.2 AMESim仿真参数设置
对主从动轮设计参数相同的外啮合齿轮泵进行仿真,由其瞬时流量式(4)可知,为了获得相同的流量特性,需保证外啮合齿轮泵2和4的设计参数相同以及电机1和电机3的转速相同。设置AMESim主要仿真参数如下:外啮合齿轮泵2和4的主动轮齿数z1=9,从动轮齿数z2=9,模数m=4,压力角α=20°,齿轮宽度B=10 mm,容积效率η=0.9;溢流阀5开启压力p=25 MPa;节流阀8最大开口处直径d=6 mm。
2.3 单泵工作时液压系统的流量脉动特性研究
设置电磁换向阀6,7处于断电状态,电机1的转速为3000 r/min。此时液压系统处于单泵工作状态,卸荷回路关闭。仿真得到液压系统的流量脉动特性如图3所示。
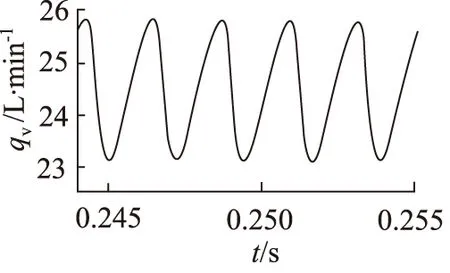
图3 单泵工作时系统的流量脉动特性
流量脉动系数:
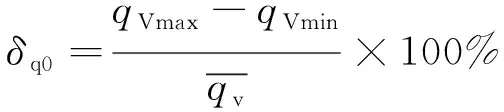
(7)
2.4 双泵合流时液压系统的流量脉动特性研究
设置电磁换向阀6处于通电状态,电磁换向阀7处于断电状态,电机1和电机3的转速均为1500 r/min。此时液压系统处于双泵合流工作状态,卸荷回路关闭。
调整齿轮泵2的齿轮初始啮合位置为啮合点与节点重合的位置(即f=0,此时齿轮泵2输出流量最大),定义齿轮泵4齿轮初始啮合位置相对齿轮泵2齿轮初始啮合位置偏差的角度为错位角θ。因为齿轮泵每对齿啮合过程输出的流量特性相同,所以选取错位角θ的范围使得齿轮泵4齿轮初始啮合位置在一对齿的完整啮合范围内变化,因此进行双泵合流流量脉动特性研究即可。由图1可知,一对齿完整啮合过程对应的齿轮泵转角φ为-π/z~+π/z。因此选取θ=-π/z~+π/z=-20°~+20°,仿真得到θ每增加5°时双泵合流液压系统对应的流量脉动特性,如图4所示。
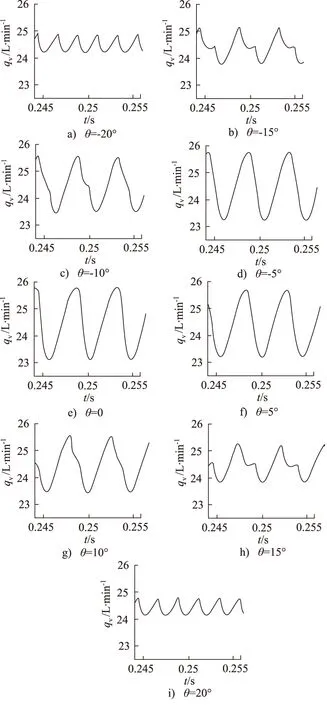
图4 双泵合流θ取不同值时,系统流量脉动特性
根据式(6)计算得到相应的流量脉动系数δq如表1所示。

表1 错位角θ-流量脉动系数δq
由此可得到双泵合流时,系统的流量脉动系数δq随错位角θ的变化如图5所示。
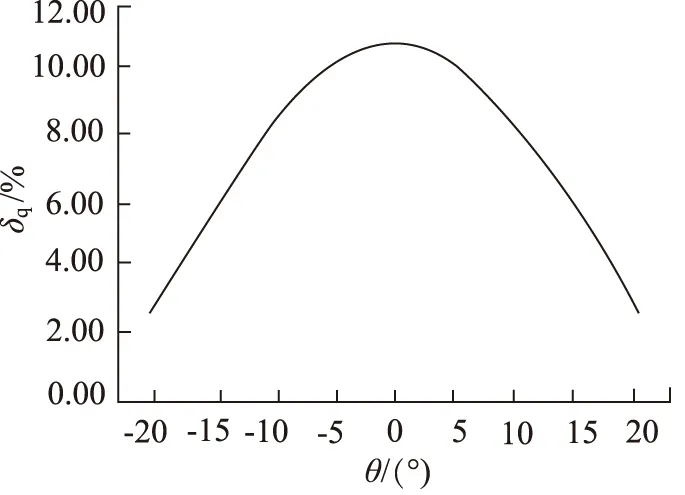
图5 θ=-20°~+20°时,流量脉动系数随错位角的变化
2.5 仿真结果分析
当液压系统处于双泵合流工作状态时,液压系统的实际流量等于外啮合齿轮泵2和外啮合齿轮泵4输出的实际流量之和。
当错位角θ=±20°时,齿轮泵4齿轮初始啮合位置处于一对齿刚开始啮合或啮合刚结束的位置,此时齿轮泵4输出的瞬时流量最小,而齿轮泵2齿轮初始啮合位置为啮合点与节点重合的位置,此时齿轮泵2输出的瞬时流量最大。当齿轮泵2和齿轮泵4同时以相同转速开始工作后,齿轮泵2输出瞬时流量最大时,齿轮泵4输出瞬时流量最小,双泵合流后,液压系统的流量脉动系数δq为最小值2.69%,远小于单泵工作时的10.78%,此时液压系统的流量脉动得到最有效的改善。
当错位角θ=0时,齿轮泵2和4齿轮初始啮合位置均为啮合点与节点重合的位置,此时齿轮泵2和4输出瞬时流量均为最大值。当齿轮泵2和4同时以相同转速开始工作后,齿轮泵2输出瞬时流量最大时,齿轮泵4输出瞬时流量也最大,双泵合流后,液压系统的流量脉动系数δq为最大值10.83%,与单泵工作时的10.78%相差不大,此时液压系统流量脉动并未得到改善。
当错位角θ=-20°~0时,双泵合流后,液压系统的流量脉动系数δq值随错位角θ的增大而增大;当错位角θ=0~20°时,双泵合流后,液压系统的流量脉动系数δq值随错位角θ的增大而减小。液压系统流量脉动改善情况介于前面两种情况之间。
仿真结果表明,采用2个设计参数相同的外啮合齿轮泵合流,在两齿轮泵转速相同的前提下,通过调整两齿轮泵齿轮初始啮合位置相差的角度,可以有效降低液压系统的流量脉动。
3 双泵合流液压系统AMESim-Simulink联合仿真
3.1 AMESim-Simulink联合仿真原理
在AMESim中搭建的双泵合流液压系统物理模型如图2所示,系统可以通过接口模块将流量计9测得的流量信号传递给Simulink,同时Simulink中输出的转速信号也可以通过接口模块传递回系统,用于控制电机1和电机3的转速。
AMESim中创建的接口模块,编译后可生成供Simulink使用的S函数[13]。在Simulink中,打包好的AMESim模型被看成一个普通的S函数[14]。MATLAB中提供了模糊逻辑工具箱,可用来建立、编辑和观察模糊控制器。利用Simulink库中的“Fuzzy Logic Controller”模块可以实现模糊控制器与Simulink的连接[15]。基于以上理论基础建立的模糊控制联合仿真模型如图6所示。
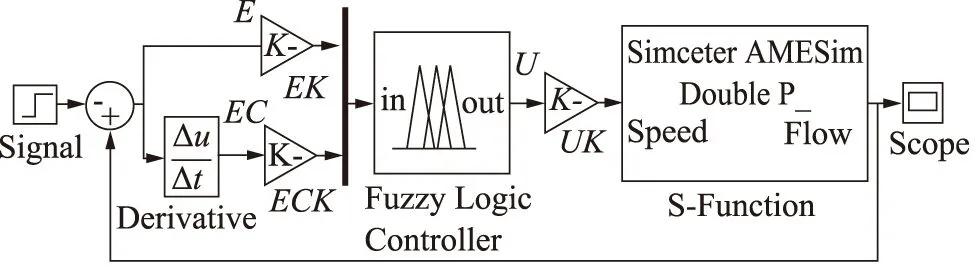
图6 基于模糊控制的AMESim-Simulink联合仿真模型
3.2 模糊控制器设计
模糊控制器的输入语言变量选择为液压系统实际流量值与设定流量值之差e及其变化率ec;输出语言变量为液压系统中电机1和电机3的转速u。即双泵合流液压系统选用1个双输入单输出的模糊控制器。图6中,E,EC和U分别为e,ec和u的模糊语言变量,EK、ECK和UK为量化因子[16]。
选定E的论域为[-6,+6],语言值为:NB、NM、NS、Z、PS、PM和PB,隶属度函数如图7所示。
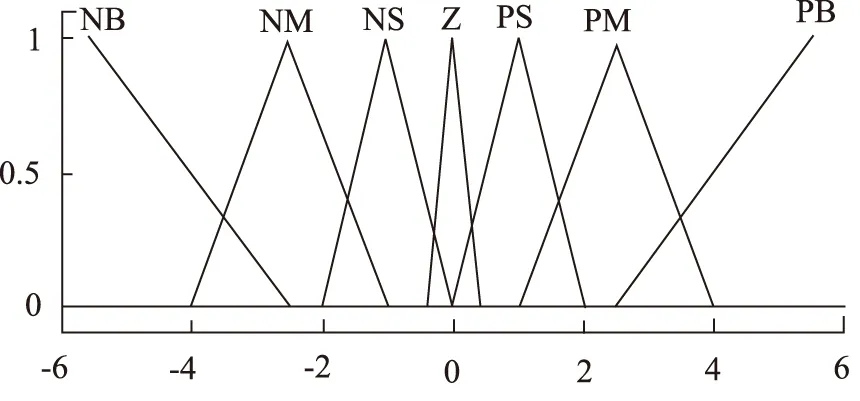
图7 模糊语言变量E的隶属度函数
选定EC的论域为[-3,1],语言值为:NB、NM、NS、Z、P,隶属度函数如图8所示。
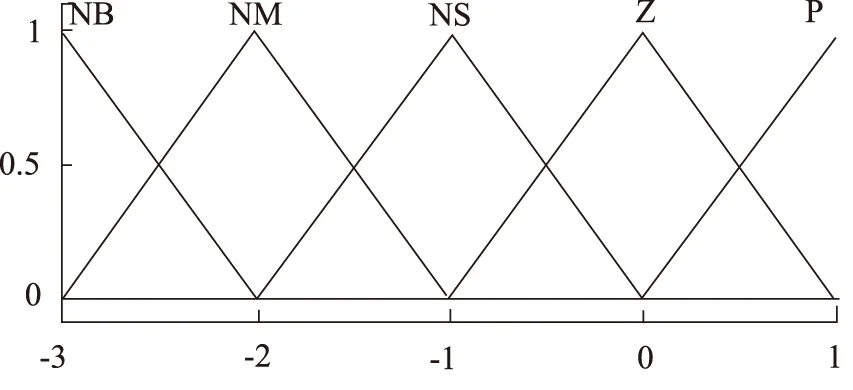
图8 模糊语言变量EC的隶属度函数
选定U的论域为[1,9],语言值为:NBB、NB、NM、NS、Z、PS、PM、PB、PBB,隶属度函数如图9所示。
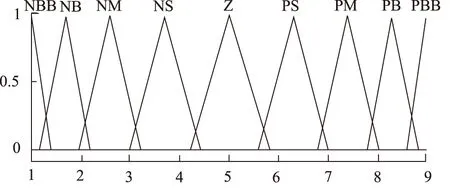
图9 模糊语言变量U的隶属度函数
由外啮合齿轮泵瞬时流量表达式(4)可知,瞬时流量与齿轮泵转速成正相关。当瞬时流量大于平均流量时,通过降低齿轮泵转度可使瞬时流量向平均流量靠拢,同理,当瞬时流量小于平均流量时,通过增大齿轮泵转速也可使瞬时流量向平均流量靠拢。基于以上的模糊控制策略,建立了双泵合流液压系统的模糊控制规则表,如表2所示。
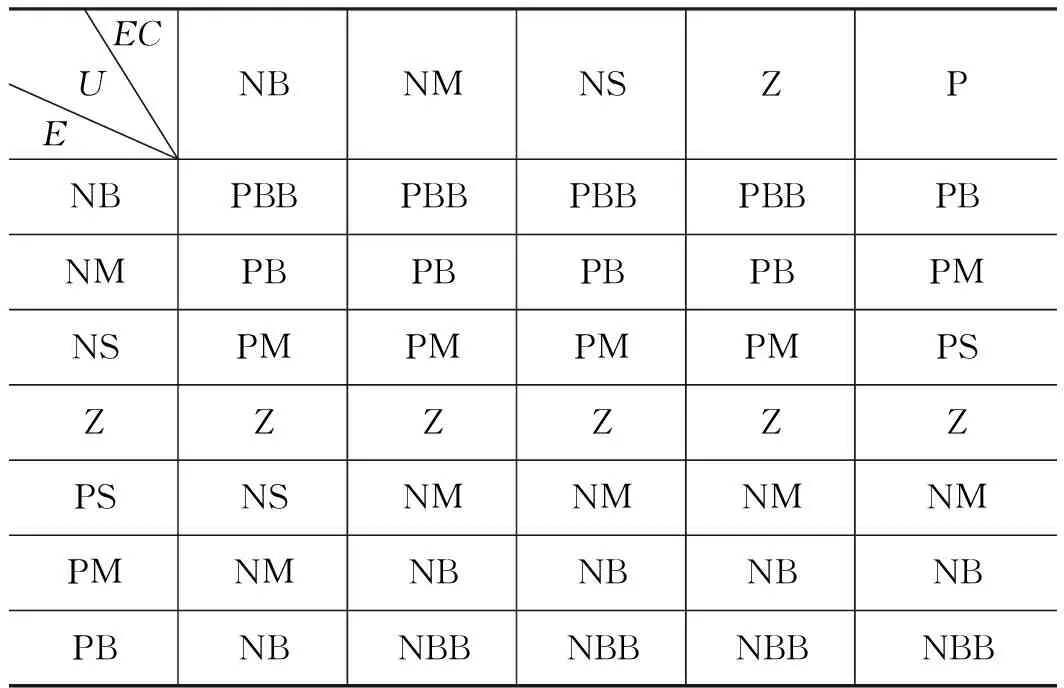
表2 模糊控制规则表
3.3 联合仿真参数设置及仿真结果分析
设置双泵合流液压系统处于双泵合流的工作状态,错位角θ=20°。流量设定值为错位角θ=20°时双泵合流液压系统的平均流量值24.56 L/min,量化因子EK=18.3598,ECK=0.0014,UK=300。运行仿真,得到基于模糊控制的双泵合流液压系统的流量脉动特性如图10所示。
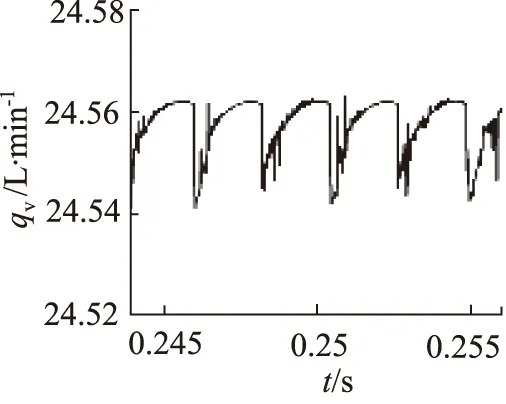
图10 模糊控制下系统的流量脉动特性
流量脉动系数:
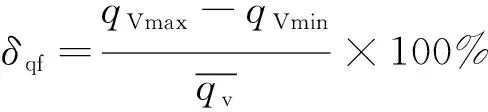
(8)
远小于不加模糊控制时的δq20°=2.69%。所以采用模糊控制器,根据系统的实际流量变化情况及时调整外啮合齿轮泵的驱动电机转速,可以有效降低液压系统的流量脉动。
通过调节节流阀开度,用于模拟负载变化引起的系统流量变化,设置节流阀开度在0.25 s时,发生阶跃变化,节流阀开度减小。得到系统的流量特性如图11所示。
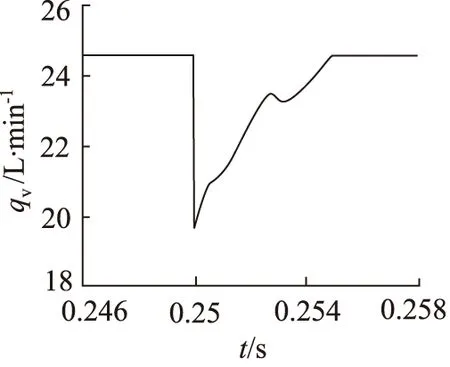
图11 节流阀开度变化时,系统的流量特性
仿真结果表明,当负载变化引起系统流量变化时,通过模糊控制器的调整可以及时将系统的平均流量调整到与设定值相同,并且流量脉动特性没有变化。
4 结论
(1) 通过对双泵合流液压系统的流量脉动特性进行仿真研究,得出了采用2个设计参数相同的外啮合齿轮泵合流,在两齿轮泵转速相同的前提下,通过调整两齿轮泵齿轮初始啮合位置相差的角度,可以有效降低液压系统的流量脉动;
(2) 在双泵合流的工作状态下,利用模糊控制器根据液压系统的实际流量变化情况,及时调整2个外啮合齿轮泵的驱动电机转速,可以有效降低液压系统的流量脉动。同时,当负载变化引起系统流量变化时,通过模糊控制器的调整可以及时将系统的平均流量调整到与设定值相同,并且流量脉动特性没有变化。
