同心圈式旋转床的气相干床压降
2020-09-15刘鹏真李育敏计建炳姜建平朱星剑
刘鹏真,李育敏,计建炳,姜建平,朱星剑
(1. 浙江工业大学 化学工程学院,浙江 杭州 310014;2. 浙江华科化工设备有限公司,浙江 杭州 310012)
超重力床通过转子高速旋转产生的离心加速度来模拟超重力环境,核心在于对传递过程的极大的强化[1]。超重力床应用于精馏[2-4],纳米材料制备[5],吸收[6]等化工领域。传统的超重力床一般采用填料结构转子[7],转子高速旋转产生的离心力导致填料内疏外密,降低了传质效率。折流式旋转床采用特殊的动静折流圈群相互嵌套的板式结构转子[8],该结构增加了液体在静折流圈上液膜传质,提高了折流式旋转床液相传质系数,但该结构导致气体在转子内做上上下下的折流式运动,造成气相压降偏大。同心圈式旋转床[9]依然采用板式结构转子,转子由一组同心圈构成,同心圈上布满筛孔。与折流式旋转床相比,同心圈式旋转床具有压降小和通量大的优点。浙江工业大学[10]对不同结构的同心圈式旋转床进行了精馏的实验研究,获得了同心圈式旋转床的等板高度。Li等[11]对同心圈式旋转床建立气液比表面积和传质系数模型,采用精馏的实验数据对模型进行了验证。
气相压降是超重力床的重要性能之一,许多研究者对其进行了相关的研究。Zheng等[12]认为转子中心喷射的液体降低了转子中心区域的气体切向速度,导致旋转床气相湿床压降小于气相干床压降;李振虎等[13]将旋转床的压降分为五个部分进行模型研究,模型预测值和实验值吻合较好;Li等[14]建立了基于气体周向速度的压降模型,合理地解释了转子气相湿床压降低于转子气相干床压降(ΔPR)的现象;Neumann等[15]提出了基于扩展通道的修正压降模型,对旋转填料床气相干床压降进行了合理的估算。Hugo等[16]运用CFD的Ergun型半经验关联式对气相压降进行分析和研究。在液量不太大的情况下,超重力床的气相湿床压降均小于气相干床压降。
本工作研究了同心圈式旋转床ΔPR,建立了ΔPR双参数模型并通过实验对模型进行验证。为同心圈式旋转床的工业设计和应用提供了理论依据。
1 实验部分
1.1 同心圈式ΔPR模型
气体通过同心圈式旋转床ΔPR可分为三个部分:气体从转子外缘向内缘流动因流道截面变小而导致的压降(ΔPm)、离心压降(ΔPc)及摩擦压降(ΔPf)[14],见式(1)。
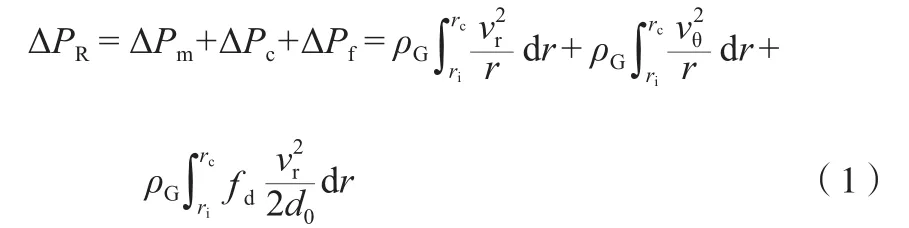
式中,ρG为气体密度,m3/kg;r为转子半径,m;ri为转子内缘半径,m;rc为转子外缘半径与旋转床腔体内缘半径的平均值,即rc=(ro+rn)/2,m;ro为转子外缘半径,m;rn为旋转床腔体内缘半径,m;vr为气体径向速度,m/s;vθ为气体周向速度,m/s;fd为干床阻力系数,无因次;d0为同心圈小孔直径,m。
Li等[14]通过实验证明转子内部vθ大于转子线速度(ωr),由此建立同心圈式旋转床ΔPR模型。转子内部vθ随转子半径(r)的增大而增大,vθ基本与ωr平行;转子外部vθ随r的增大而急剧下降,在rc处vθ等于气体进口管的气速(uin)[14]。本工作对真实vθ的径向分布进行简化可知:转子内部vθ随r的增大而线性增大,vθ与ωr平行;转子外部vθ随r的增大而线性减少。定义vθ与ωr的差为气体相对周向速度(vθS),见式(2)。
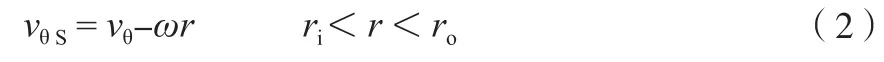
简化的vθ分为转子内部和转子外部两部分,见式(3)。

式中,vθB为转子外缘处的气体周向速度,m/s;ω为角速度,rad/s。
气体径向速度(vr)按式(4)计算。

式中,QG为气体流量,m3/s;h为转子轴向高度,m;φ为开孔率,无因次。
旋转床uin按式(5)计算。

式中,din为旋转床气体进口管的内径,m。
将式(3)和式(4)代入式(1)并积分得到ΔPR的表达式,见式(6)。

结合式(6)和式(7)即为同心圈式旋转床ΔPR模型,该模型含有fd和vθS两个参数。定义fd为转子不旋转时气体通过转子产生的摩擦压降的干床阻力系数,则fd仅是QG的函数。
基于转子平均半径处气体流通面积的气体速度为平均表观气速(uGP),见式(8)。

式中,rp为转子平均半径,rp=(ri+ro)/2。
基于气体平均表观速度的气体雷诺数(ReG)和基于转子平均半径的旋转雷诺数(Reω)的表达式,见式(9)和式(10)。


式中,μG为气体黏度,Pa·s。
fd与ReG相关,采用幂指函数关联,见式(11)。

当转子不旋转时,ω,vθS,vθB都为 0,则ΔPc≈0。忽略ΔPc,则式(6)可简化为式(12)。

将实验数据QG和ΔPR带入式(12)得到fd。用fd和QG的数据对式(11)进行拟合得到a1和b1。将fd带入式(6),把实验测得的ω,QG,ΔPR的数据代入式(6)和式(7),得到vθS。vθS是QG和ω的函数,采用无因此准数关联,得到式(13)。

对式(13)进行拟合,得到a2,b2,c2。
1.2 实验装置
图1为实验用的同心圈式旋转床的结构示意图。由图1可知,旋转床转子由上圆盘、下圆盘和31个布满圆孔的同心圈组成,下圆盘和旋转轴固定,液体分布器位于转子的中央,同心圈、下圆盘、上圆盘和液体分布器随旋转轴一起转动。旋转床转子内径为400 mm,外径为1 000 mm,轴向高度为100 mm。同心圈上开有直径为1.8 mm的圆孔,孔间距2.8 mm。

图1 同心圈式旋转床结构示意图Fig.1 Schematic diagram of concentric-ring rotating bed.
图2为实验流程。由图2可知,同心圈式旋转床与风机相连,空气经涡街流量计计量后从旋转床的气体进口切向进入壳体,由转子外缘向转子内缘流动,最后从气体出口流出旋转床。旋转床转子的转速由变频器进行调节。U型压差计一端位于转子内缘处,一端位于转子外缘处,测量不同转速(包括转子不旋转)和不同气量(包括不通气体)下的ΔPR。为了与其他超重力床比较,实验还测量了同心圈式旋转床气相进口和气相出口之间的全床气相干床压降。

图2 实验流程Fig.2 Sketch of the experimental setup.
基于转子内缘流通面积的表观气速(uG)的表达式见式(14)。

超重力因子(β)为旋转床的平均离心加速度与重力加速度之比,见式(15)。

2 结果与讨论
2.1 表观气速和超重力因子对ΔPR的影响
图3为uG和β对旋转床ΔPR的影响。由图3可知,在相同β下,ΔPR随uG的增大而增大,这是因为随气量的增大,vr随之增大,导致ΔPf增大,进而ΔPR增加。β=0时的ΔPR远小于β>0时的ΔPR,这是因为转子不旋转时的ΔPc为0,故而ΔPR下降。ΔPR随β的增大而增大,这是因为转速增大,转子内vθ随之增大,导致转子ΔPc增大,进而ΔPR增大。无气量(uG=0)时的ΔPR小于有气量(uG>0)时的ΔPR,这是因为无气量时ΔPf为0,故而ΔPR下降。在uG=0~6.63 m/s,β=0~562.83的范围内,ΔPR=250~5 620 Pa,即转子气相干床每米压降(ΔPR/(ro-ri))为0.83~18.73 kPa/m。

图3 ΔPR随uG(a)及β(b)的变化Fig.3 Change in rotor dry bed pressure drop(ΔPR) with superficial gas velocity(uG)(a) and high gravity factor(β)(b).
2.2 与其他类型超重力床全床气相干床压降比较
表1为同心圈式旋转床与泡沫金属填料旋转床、折流式旋转床的全床气相干床压降比较。为了较为全面的比较不同类型旋转床的压降,选择填料式、折流式两种不同类型的旋转床,在相近的操作条件下,比较了不同类型旋转床的全床气相干床压降和每米压降。由表1可知,在旋转床转速约为1 000 r/min、气量约为2 m/s时,同心圈式旋转床的全床气相压降为2 745 Pa,虽然相比其他两种类型的旋转床较大,但具有较大的转子尺寸,表明同心圈式旋转床可达到更大的通量,适合于大通量的工业化应用。同时,每米压降较小,在相近的操作条件下,同心圈式旋转床每米压降为9.15 kPa/m,比泡沫金属填料旋转床低38.47%,比折流式旋转床低34.60%。说明同心圈式旋转床具有干床压降小的优点。
2.3 ΔPR模型关联
图4为vθS随QG和n的变化曲线。

表1 与其他类型超重力床全床气相干床压降比较Table 1 Comparison of the overall dry bed gas pressure drop with other high gravity rotating bed

图 4 vθ S 随 QG(a)和 n(b)的变化Fig.4 Change in gas relative circumferential velocity(vθ S) with gas flow rate(QG)(a) and n(b).
由图4可知,vθS随QG增大而增大,但随n增大vθS却基本不变。
利用实验数据对式(11)和式(13)进行拟合,得到参数a1,b1和a2,b2,c2,见式(16)和式(17)。

图5a为正负偏差在15%以内,干床vθS/ωrp的计算值与实验值。由图5a可知,最大偏差为13.62%,平均偏差为3.96%。将式(16)和(17)代入式(6)中,得到旋转床ΔPR表达式。由式(16)、式(17)和式(6)可知,只需得到旋转床的结构参数和操作参数就可以计算出旋转床ΔPR。图5b为正负偏差在10%以内,ΔPR计算值与实验值。由图5b可知,最大偏差5.35%,平均偏差1.97%。因此,本工作所建立的同心圈式旋转床ΔPR双参数模型简单合理,可用于旋转床ΔPR的计算。
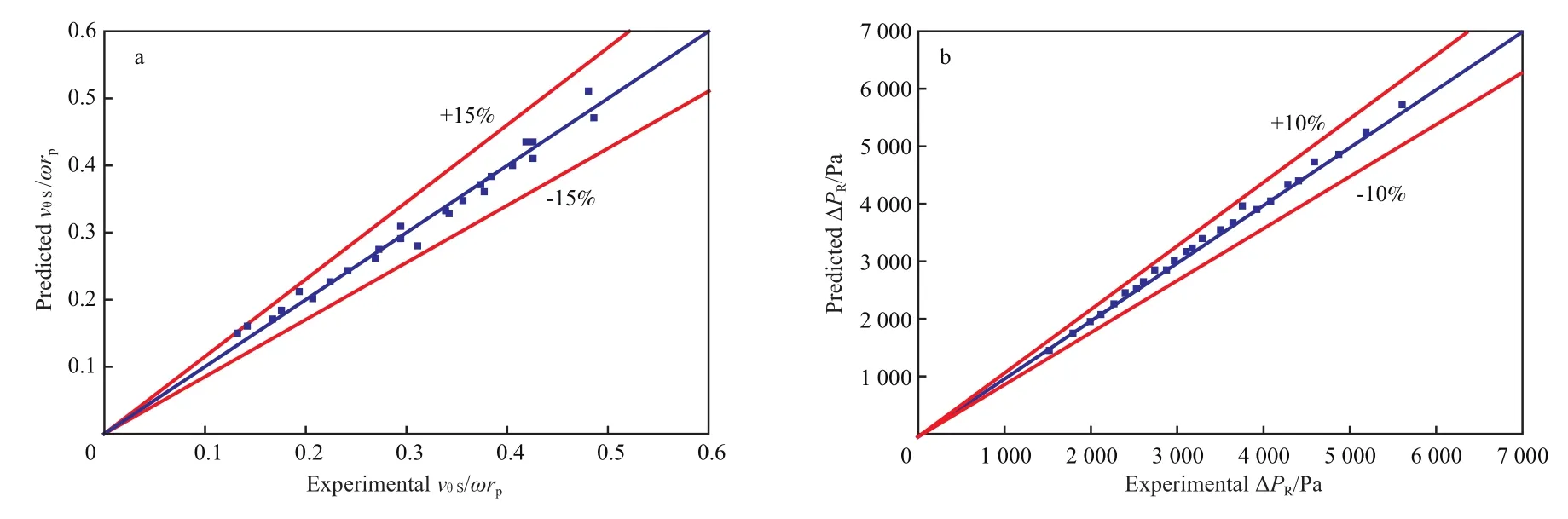
图 5 vθ S/ωrp(a)和 ΔPR(b)的计算值与实验值Fig.5 Comparison of experimental and predicted vθ S/ωrp (a) and ΔPR(b).
3 结论
1)针对vθ大于ωr的现象,引入vθS和fd建立ΔPR双参数模型,模型能较好地描述旋转床ΔPR的变化规律。
2)同心圈式旋转床ΔPR随uG和β的增大而增大;vθS随QG增大而增大,但随n的增大vθS却基本不变;在uG=0~6.63 m/s,β=0~562.83的范围内,同心圈式旋转床转子气相干床每米压降为0.83~18.73 kPa/m。
3)ΔPR双参数模型对同心圈式旋转床ΔPR进行计算,计算值和实验值平均偏差为1.97%,正负偏差在10%以内,模型的计算值和实验值吻合较好。ΔPR双参数模型简单合理,为同心圈式旋转床的工业应用提供理论依据和设计依据。

