执行器退化下反馈控制系统的寿命预测和延寿方法
2020-09-15王成文
李 炜, 王成文
(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级实验教学示范中心, 甘肃 兰州 730050)
随着工业过程安全性、可靠性要求的提升,控制系统的性能和相关设备的健康管理已成为业界关注的重点问题[1].执行器作为控制器与被控对象之间的物理连接,在反馈控制系统中扮演着重要角色,因长期运行及外界环境的影响,不可避免地会发生腐蚀、磨损、冲击等退化问题,从而减弱执行器的执行能力,降低控制系统性能,影响产品质量[2].如若在其退化初期就能对系统的寿命进行预测,并采用适当的控制策略通过延缓执行器的退化过程进而延长控制系统的寿命,这对企业的安全生产具有重要意义[3].因此,控制系统剩余寿命预测(residual useful life,RUL)以及延寿控制已成为预测与健康管理(prognostics and health management,PHM)领域高度关注的问题.
控制系统在高性能要求的运行过程中,执行器作为关键部件通常是满负荷甚至过负荷工作.因此,这类关键部件的退化必定会影响控制系统寿命和系统的维护时间.
目前,针对执行器等部件退化的剩余寿命预测已取得了大量的研究成果,但对控制系统寿命预测和健康管理方面的研究还相对较少.Khorasgani等[4]指出,虽然执行器寿命与控制系统寿命存在本质区别,但执行器性能的逐渐退化必然会导致系统性能下降.因而,若仅就执行器退化情形下,建立更为准确的退化过程模型对控制系统的寿命进行预测,并据此制定合理的维护策略,是延长控制系统运行时间的关键所在.
为能在部件退化或早期故障情形下尽可能延长系统寿命、增加其可靠工作时间,延寿控制方法应用而生.它是指通过调整某些性能变量的变化率或者参数值来减小关键部件的损伤或损坏率,并保证系统性能处于可接受范围内[5].延寿控制作为一种通过改变控制作用、控制器结构或者增益来主动管理系统关键部件健康水平的在线视情维护方法,起初应用于火箭发动机的延寿中[6],后逐渐在其他执行器的健康管理中出现.
Langeron等[9]研究了执行器服从Gamma退化过程下的反馈控制系统延寿策略,通过调整控制器参数保证系统更长的运行时间,但在执行器退化过程建模时仅考虑了冲击影响且只针对某一退化阶段进行延寿控制研究.
Weber等[10]针对执行器退化情形提出了新的控制分配策略,通过在线对执行器可靠性进行评估并设计补偿调节器,通过修正设定点延长系统运行寿命,但同样缺乏对执行器退化机理的全面分析.
施权等[11]将闭环反馈控制作用下的执行器退化描述为隐含退化过程,建立了控制系统剩余寿命与执行器退化过程的内在联系,基于粒子滤波与蒙特卡洛方法估计得到执行器的隐含退化量和系统失效阈值,推导了系统剩余寿命分布,但未涉及执行器退化下控制系统延寿控制策略的研究.
鉴于以上分析,本文考虑到执行器退化过程机理的复杂性,建立了更贴合实际的复合退化模型;采用基于失效时间的概率方法估计控制系统剩余寿命.在此基础上,利用系统退化状态信息调整LQR控制策略寻找系统性能与控制作用之间满意的Q和R参数,通过减小控制作用来保证执行器的健康水平.同时,引入修正参考设定值的方法来避免系统达到给定退化阈值时LQR调节无效的缺陷,通过延缓执行器退化过程来延长系统的运行时间,以期在执行器退化的全周期内为控制系统提供延寿保障.
1 问题描述
1.1 执行器退化下反馈控制系统描述
考虑控制系统中执行器的类型不同及其退化过程存在差异,且多个执行器退化对系统寿命影响较为复杂.本文以单一执行器退化下的线性系统为研究对象,其状态方程可描述为
(1)
式中:x(t)∈Rn为n维状态向量;u(t)∈Rr为控制输入;y(t)∈Rm为系统输出;A、B、C分别代表系统状态矩阵、控制矩阵和输出矩阵;执行器完成控制作用u(t)的能力很大程度上取决于其健康水平;由于执行器退化量逐渐累积,完成控制作用u(t)的能力逐渐减弱,可以用(1-c(t))描述,其中c(t)={diag(0,…,ci,…,0)}r×r为第i个执行器发生退化,ci=C(t)/C(t0)表示执行器当前执行能力与初始执行能力之比.
为更精确描述执行器退化对系统性能的影响,结合执行器执行能力与系统性能之间的关系,本文将退化过程描述为图1所示的三个阶段,其中:Ln表示系统性能正常时的执行器执行能力阈值;Lsf表示执行器退化至系统失效时的阈值;Laf表示执行器失效阈值,显然lsf 阶段Ⅰ:考虑设计之初执行器留有一定裕量,此阶段执行器发生退化时,由于执行机构的设计裕量可保证系统不受退化影响,D(t)≤Ln且ci=0; 阶段Ⅱ:由于执行器持续退化,系统性能已无法达到所要求的性能指标,此阶段Ln 阶段Ⅲ:因执行器退化使系统性能处于不可接受的范围内,此阶段Lsf 在现代控制理论中,LQR因反馈控制律简单、控制过程易于实现的特点在控制工程中获得了广泛应用.LQR要求确定最优的控制作用u(t),在区间[t0,th]使以下二次型性能指标极小: (2) 式中:Q和R分别表示状态量权重和控制量权重;y(t)为实际输出;r(t)为设定参考点.根据LQR控制理论[12],系统控制作用u(t)可表示为 u(t)=-Kx(t)+[C(BlK-A)-1Bl]-1r(t) (3) 式中:K表示使性能指标最小的增益矩阵;Bl=B(1-c(t))为执行器退化下的控制矩阵. 为评价控制系统性能,本文采用静态误差ess、上升时间tr和调节时间ts三个指标衡量: (4) 执行器通常由阀门、电机等物理设备组成.在实际中,磨损和冲击是导致其遭受不同程度损伤的主要原因[13].因此,单一的退化机理并不能准确描述实际退化过程,需要借助多种退化机理共同作用的复合退化模型进行描述.此外,相比基于Wiener过程的退化建模方法,Gamma过程和累积损伤退化模型具有物理意义明确的优点[14],亦适用于磨损和冲击退化过程建模.因此,本文选择后者建立复合退化模型. 假设D(t)为t时刻执行器的退化量,在t>0的时间段内,执行器退化量可表示为 D(t)=Z(t)+S(t) (5) 其中:Z(t)表示执行器的磨损退化量;S(t)表示外界冲击造成的累积退化. 磨损过程是缓慢发生的,在许多研究中,Gamma过程样本路径包含微小的难以观察的跳跃和创伤性跳跃,常用以描述系统疲劳、磨损、腐蚀等自然退化现象[15].设Gamma退化过程为{X(t),t≥0},退化失效阈值为常量laf,T表示退化过程的首达时间,Gamma过程的概率分布函数可表示为 (6) 式中:α和β分别表示Gamma分布的形状参数和尺度参数,相应的概率密度函数为 (7) 因工况变化与工作环境影响,执行器会受随机冲击影响并造成损伤,这些损伤具有累积效应.当累积损伤超过一定范围时,就会导致系统失效[16].假设第k次冲击造成的损伤幅值为Wk,以N(t)表示直到时刻t的冲击次数,则时刻t的退化量S(t)可以表示为 (8) 在元件正常运行中,往往受到外力的冲击[17],且冲击是随机产生的,从任何时间t到下一次冲击到达的时刻具有无记忆性,则可认为冲击服从参数为λ的齐次Poisson过程,且冲击幅值服从均值为μ的指数分布,也可表示为形状参数为k、尺度参数为1/μ的Gamma分布.当产品的退化过程可以利用复合Poisson过程描述时,利用标准损伤累积过程的结果,可得t时刻累积损伤S(t)的概率分布函数为 (9) 相应的概率密度函数为 (10) 综上分析可知,在磨损与冲击作用下执行器复合退化的寿命概率分布函数可以表示为 P{D(t) (11) 若假设执行器的初始执行容量为Ca,t时刻的退化量为D(t),则该时刻执行器的执行能力可表示为 C(t)=Ca-D(t) (12) 执行器寿命和控制系统寿命既有区别又有联系.执行器寿命虽然仅反映单个器件的生命周期,但当其退化到某一阈值时系统也将无法完成期望的控制任务,即意味着控制系统寿命终止[11].因此确定不满足性能指标的控制系统退化阈值,并依据此进行寿命预测和在线延寿维护是本文要解决的核心问题. 所有28例宫颈腺癌患者采用体外放射治疗加腔内放射治疗,体外放疗应用60 Co远距离体外放射治疗机,体外全盆野照射总量45~50 Gy,腔内照射应用192Ir后装治疗机,总量24~30 Gy。放疗结束后,根据患者的具体情况于3~12周行经腹手术,其中7例患者于放疗后4周内行手术,20例患者于放疗后4~8周行手术,1例患者于放疗后12周行手术;筋膜外全子宫及双附件切除术26例,筋膜外全子宫、双附件切除术及部分阴道切除术1例,筋膜外全子宫、双附件切除术及盆腔淋巴结活检术1例。 由于lsf Tf=inf{t:D(t)>lsf} (13) 则系统剩余寿命表示为 RUL(t)=inf{Tf>t,D(t)>lsf}-t (14) 由已建立的复合退化模型可知,系统的剩余寿命概率分布函数为 F(t)=P{T≤t}=P{Z(t)+S(t)>lsf}= P{D(t)>lsf}=1-P{D(t)≤lsf}= (15) 其对应的概率密度函数可表示为 (16) 综合式(13~16)可得系统剩余寿命预测信息,这为延寿控制为主的在线视情维护提供了前提条件.若将执行器的健康水平和系统剩余寿命纳入控制器设计中,通过调整控制策略来管理执行器退化,便可保证整个控制系统在可接受的性能要求下运行更长时间. 由前述线性二次型调节器(LQR)性能函数可知.Q强调状态量对系统性能的影响,R关注控制输入与性能指标的关系.权重Q减小和R增大可使控制输入减小,以此缓解执行器的执行压力,进而达到延缓执行器退化并延长系统寿命的目的.然而,当因执行器退化使系统无法按期望目标完成任务时,为保证控制系统能够延长安全工作时段,可以通过调节参考设定值来达到延长控制系统寿命的目的.延寿控制下的反馈控制系统结构如图2所示.针对前述执行器退化导致系统退化的三个不同阶段,控制系统的延寿策略亦分为三个阶段. 具体的算法流程如图3所示. 单容水箱控制系统是一个典型的反馈控制系统,本文通过研究其水泵的退化过程来验证文中方法的有效性.设水箱的横截面积为S,入口流量qin与水泵的控制输入uc之间的关系为 qin=Ka·uc 式中:Ka表示水泵的执行能力. 根据托里拆利定理,出口流量为 式中:h表示水箱液位高度;g为重力加速度;Kv为阀门相关参数. 根据质量守恒定律建模并进行近似处理,可得单容水箱系统的模型为 (17) 本文假定磨损退化服从尺度参数为μ的指数分布,冲击时间服从参数为λ的齐次泊松过程,且每次冲击的损伤也服从尺度参数为μ的指数分布.复合退化模型下,控制系统的寿命分布表示为 F(t)=P{D(t)>lsf}=P{Z(t)+S(t)>lsf}= (18) 同时,为比较延寿策略与无延寿策略下的反馈控制系统性能指标,选择执行器退化的全过程中N个退化点进行仿真分析.则评价系统的三个关键性能指标可定义为 (19) 1) 执行器复合退化模型及系统剩余寿命预测 因实际执行器退化过程的复杂性,多种退化机理相比单一的退化机理对其描述更为准确.本文仿真了磨损和复合情形下的执行器退化曲线,从退化机理角度阐述了单一退化和复合退化模型对执行器退化描述的差异.从图4可知,因复合退化模型同时考虑磨损和冲击的影响,相比单一的磨损退化对执行器退化描述更为贴合实际. 由1.2节的描述可知,在退化过程中执行器的执行能力会随之下降.假设执行器的初始执行能力为Ka=8,根据式(12),复合退化情形下执行器执行能力随时间的变化曲线如图5所示. 在执行器执行能力因退化而下降的过程中,控制系统性能也会随之下降,当超过控制系统三个性能指标约束对应的退化失效阈值lsf时,根据式(18)和lsf,此时单容水箱控制系统的寿命预测分布如图6所示.从图6可知,在t=95 s时系统无法满足性能指标,即说明控制系统寿命终止. 2) 控制系统延寿策略 为说明执行器退化情形下,延寿策略与无延寿策略时对控制系统输出的影响,仿真给出了图7所示的对比图.可以看出在执行器随时间发生退化时,系统输出呈现逐渐下降的趋势.但是,在延寿策略下执行器的执行压力得到缓解,系统输出更为理想.进一步,当执行器退化达到阈值lsf时,通过调整控制器参数已无法缓解执行器执行压力,此时,需适当降低控制目标,通过修正参考设定值,牺牲系统的性能指标换取执行器的健康水平(框线部分所示),以此进行控制系统延寿控制. 延寿策略与无延寿策略时系统性能的对比结果见表1,表明延寿策略下不仅能保证执行器健康水平,系统性能也可在接受范围内.同时,在延寿策略下Tr和Ts略大于无延寿策略时,也说明为了保证执行器健康水平,必须以适当牺牲部分系统性能为代价. 表1 系统性能对比 图8显示了延寿策略与无延寿策略下控制作用的变化曲线.延寿策略下,控制作用随退化时间逐渐减小,执行器执行压力能够有效缓解,因此可以延长系统的运行时间;而未采取延寿策略时,由于控制器持续施加相同的控制作用,执行器执行压力无法得到缓解,系统寿命也因此减少.延寿策略下Q和R的变化趋势如图9所示. 延寿策略与无延寿策略下执行器执行能力对比结果如图10所示,显然,延寿策略下执行器的退化过程较未延寿时缓慢,证明所提方法能缓解其执行压力并有效延长系统运行时间. 本文针对执行器退化情形下LQR反馈控制系统的寿命预测及系统在线自主优化维护问题,建立了执行器随机复合退化模型,并根据执行器退化过程定义了系统退化的三个阶段,采用基于失效时间的概率方法预测控制系统寿命.为实现系统在线自主优化维护并延长系统运行周期,通过折衷平衡执行器健康水平和控制系统性能,提出了调整LQR控制器参数和修正设定值的延寿策略来保证系统获得更长的运行时间.仿真实验表明,所提方法能够通过减小执行器控制输入保证其健康水平,进而延长系统工作寿命. 下一步研究工作主要包括:1) 对执行器寿命和控制系统寿命进一步细致区分,探究二者之间的区别与联系;2)寻找新的延寿控制策略对执行器退化下的控制系统进行延寿控制.1.2 执行器退化过程描述
2 控制系统剩余寿命与延寿控制策略
2.1 控制系统剩余寿命预测
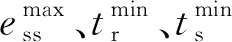
2.2 控制系统三段式延寿策略
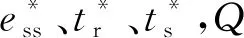
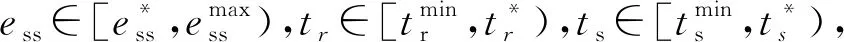
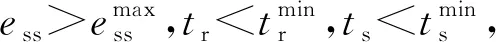
3 仿真实验与结果分析
3.1 仿真实验
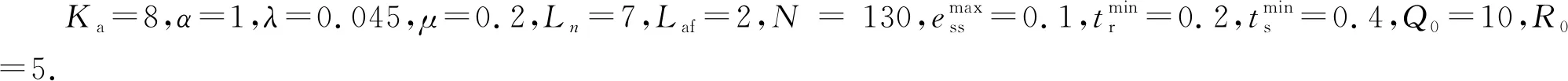
3.2 结果分析

4 结语
