基于功率流法的地铁轨道振动能量分布特性研究

席 锐

(华东交通大学土木建筑学院，江西 南昌 330013)

功率流概念的提出起源于1980年，由Goyder.H.G.D最先提出，随后被广泛应用于振动能量的特性研究。在此基础上，又发展出了许多应用功率流理论的具体方法。目前，功率流理论在航天、船舶和机械等等领域得到了广泛的关注，一般多用于振动噪声控制[1]、振动能量的传播路径识别[2]和主被动振动控制[3]等等研究。

轨道领域的学者也从振动能量的角度分析轮轨关系和动力响应的问题。汪力为研究扣件系统橡胶垫刚度匹配问题，通过谐响应分析和功率流理论，从振动能量的角度给出了双层刚度匹配的建议[4]。徐宁建立了4种车辆—轨道垂向动力学模型，给出了系统各部件之间的功率流传递函数的解析解，并分析了车辆一系悬挂、二系悬挂、轮轨间以及钢轨和轨枕间的振动功率流传递特性[5]。周昌盛考虑了不平顺对轮轨耦合振动的影响，采用有限元功率流的方法，对比了加速度和功率流用于评价减振方面的区别[6]。以上研究对地铁隧道轨道关注较少，地铁因为引入减振轨道，从而振动能量在轨道结构中的传播特性变得更加复杂，因此对地铁隧道减振轨道的振动能量传递机理的研究十分有意义。

1 计算模型及功率流方法

1.1 计算模型

基于车辆—轨道耦合动力学理论，建立地铁隧道钢弹簧浮置板轨道计算模型，如图1所示为准确反映道床板与衬砌的振动特性，两者均采用实体，将钢弹簧浮置板简化为阻尼弹簧，约束模型水平面内的位移与水平面外的转动。为消除边界效应，模型长度取32 m，计算模型如图1所示。

车辆与轨道耦合关系通过轮轨相互作用力来实现。从下式可求得垂向轮轨力：

其中，[βT]为轨道系统在轮轨接触点处的原点垂向位移导纳；[βW]为单节车辆在轮对处的柔度矩阵；[βH]为轮轨接触弹簧的动柔度，[βH]=1/kH。

利用ANSYS软件建立钢弹簧浮置板轨道—衬砌有限元模型。在有限元模型中，钢轨采用Beam188单元；扣件与钢弹簧以Combin14单元进行模拟；浮置板采用Soild45实体单元。轨道模型动力学参数如表1所示。ANSYS模型如图2所示。

表1 轨道模型动力学参数

将上面求得的轮轨力作为系统的输入，当地铁A型车以时速80 km/h的速度通过时，仅考虑轮轨间的竖向接触。

1.2 功率流方法

计算频域内的稳态功率流通常采用稳态功率流，频域稳态功率流的计算公式为：

其中，F为力在频域的复数值；V为速度在频域的复数值；Re表示取实部，上标*表示取共轭。导纳功率流P(ω)的单位为：N·m/s，即W。

在ANSYS软件中得到有限元模型中各个阻尼弹簧单元的力和各个节点的速度，再计算得到各个计算点的功率流。

最后可按以下公式进行求和计算：

其中，i为所求功率流的节点序号；n为节点总数；k为计算频率点，Hz。取一块轨道板长度(6.5 m)内的钢轨、轨道板(道床板)、衬砌节点计算功率流，并进行求和得到总功率流。

2 计算结果及分析

2.1 地铁隧道减振轨道振动能量传递特性

地铁隧道减振轨道功率流如图3所示。根据查阅相关文献能得出结论，200 Hz为钢轨竖向弯曲的第一阶模态。由图3可得，钢轨、道床板和衬砌层功率流的第一个峰值恰好出现在200 Hz左右，道床板和衬砌在1 600 Hz附近达到第二个功率流峰值。由此可得，当钢轨、道床板和衬砌三者发生耦合振动，其固有频率为200 Hz，三者功率流的峰值出现在200 Hz。钢轨的振动与道床板和衬砌的振动在200 Hz～1 000 Hz范围内解耦。1 600 Hz为道床板与衬砌耦合振动的固有频率，在此处二者功率流同时达到峰值。道床板与衬砌的功率流一般维持在比较低的数字。由图3还能得出，在减振轨道结构内，功率流的数值是不断逐渐衰减，尤其是在从上往下传递的过程中。深入探究其背后的原因，是因为振动能量会因为扣件和减振装置有所衰减。

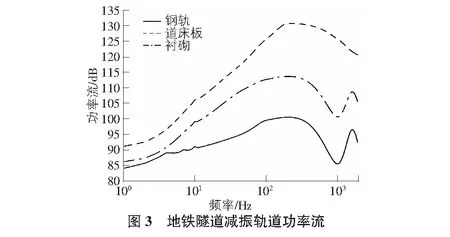
功率流在实际传递过程中会发生一定的衰减，被各层结构储藏或者耗散。扣件具体作用于钢轨上，不但会对钢轨的功率流产生影响，同样会对道床板的功率流产生影响，两者之间的差值就是振动能量在地铁隧道减振轨道的传递过程中，因为扣件的减振作用，发生了衰减，不但如此，连衬砌的功率流也会受到一定的影响，这之间的差距表达的是减振装置起到的作用，因为有了减振装置的减振作用，振动能量在对地铁隧道减振轨道传递的过程中也会发生衰减。比较流入钢轨的功率流与流入道床板的功率流可得，激振频率不断增大时，无论是低频还是中高频，流入钢轨的功率流与流入道床板的功率流衰减量都是逐渐增大。振动能量在钢轨与道床板之间的衰减在1 Hz处为10 dB，随着频率逐渐增大，衰减量也越来越大。在中低频范围，振动能量从钢轨流入道床板时，发生衰减，衰减的幅度随着频率的增加呈现上升的趋势。而在中高频范围内，振动能量从钢轨流入道床板时，同样会发生衰减，且衰减量与中低频相比较略有增大。通过分析，这其中的原因主要是扣件的弹性与阻尼都会影响振动能量从钢轨流入道床板发生的衰减。在中高频范围，扣件这一作用得到了更为显著的体现。

在中低频范围，通过比较输入道床板和衬砌的功率流，可以看出，这两层结构的能量差距与激振频率有着直接的关系。当激振频率变大的时候，输入道床板和衬砌的功率流的能量差距慢慢增大。道床板和衬砌之间的振动能量衰减在中低频范围下，随着频率的增大，振动能量的衰减量翻了10倍以上。在中高频范围内，当激振频率呈现增大势时，输入道床板和衬砌的功率流差距没有变化。这是因为衬砌与道床板之间的振动能量衰减是因为减振装置的弹性与阻尼发挥作用。

2.2 轨道结构参数对功率流的影响

扣件在对振动能量的竖向传递中起到了至关重要的作用，分别设置不同的扣件刚度、阻尼以及减振装置的刚度，通过对比地铁隧道减振轨道中输入钢轨、道床板和衬砌的功率流，揭示振动能量的竖向传递中受扣件带来的影响。

2.2.1扣件刚度的影响

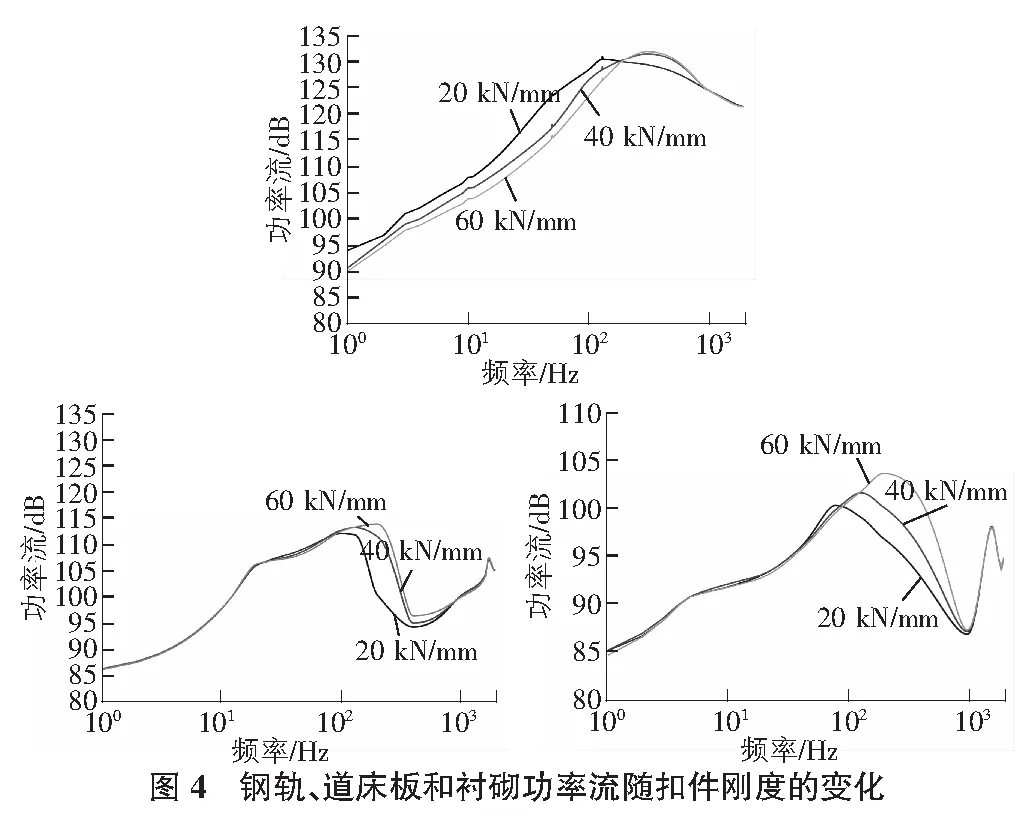
图4为道床板、钢轨与衬砌的功率流随扣件刚度的变化而变化。从图4可得，在低频范围内，钢轨功率流随着钢轨功率流的增大慢慢减小。扣件刚度从20 kN/mm增大到60 kN/mm时，钢轨功率流没有太大变化。说明钢轨功率流在低频范围内，对扣件刚度的变化不是十分敏感。除此之外，钢轨功率流峰值出现的频率变大，往往伴随着扣件刚度的变大。调整扣件的刚度，从20 kN/mm增大到60 kN/mm时，钢轨功率流峰值有明显的增幅。

在中高频范围，向增大的趋势调整扣件的刚度，输入道床板的功率流传递变大，在高频范围内，扣件刚度增加，道床板功率流的增幅变小。调整扣件的刚度，从20 kN/mm增大到60 kN/mm时，在中高频范围内，道床板功率流增大的范围有限，约为一成，说明道床板功率流对扣件刚度的变化不是十分敏感。

在中高频范围，传递到衬砌的功率流随着扣件刚度增大而增大，在高频范围内，调整扣件刚度的大小，衬砌功率流对应扣件刚度的变化幅度开始减小。衬砌功率流峰值出现向右移动。扣件的刚度变大，从20 kN/mm增大到60 kN/mm时，衬砌功率流峰值有一个较大幅度的提升。在中高频范围内，调整扣件的刚度，从20 kN/mm增大到60 kN/mm时，衬砌功率流变化的幅度不足10%。

2.2.2扣件阻尼的影响

图5为钢轨、衬砌与道床板功率流随扣件阻尼的变化。从图5可得，扣件阻尼的变化同样影响着钢轨功率流在中高频出现的峰值大小，当扣件阻尼变大，钢轨在中高频出现的峰值功率流明显变小。同时，扣件阻尼增大，钢轨功率流在中频处的峰值会随之减小，调整扣件阻尼，一样会影响钢轨功率流出现的峰值大小。当扣件阻尼变大，从图中可以看到，钢轨功率流的峰值变小。可得，扣件阻尼主要对钢轨功率流的改变发生在中频范围内。除此之外，钢轨功率流的最小幅值也受到扣件阻尼的影响，钢轨功率流随着扣件阻尼的变大而变大。

扣件阻尼对道床板功率流的影响范围主要集中在中高频范围内。道床板功率流峰值受扣件阻尼的影响较大，具体表现为扣件阻尼增大时，在中频范围内道床板功率流峰值有了明显的减小。由此可得，道床板中频范围内的振动能量受到扣件阻尼的显著影响，具体表现为，扣件阻尼增大时道床板功率流峰值会发生减小。但是，扣件阻尼对道床板功率流影响在低频频率范围内几乎没有。

衬砌对扣件阻尼有一定的敏感度，当扣件阻尼增大时，衬砌功率流在中高频范围内会产生较大的衰减。由此可得，衬砌的振动能量受到扣件阻尼的影响，且效果显著，当扣件阻尼增大时，衬砌功率流在中高频范围内会产生较大的衰减。在低频频率范围内，衬砌功率流几乎不受到扣件阻尼的影响。

3 结语

本文计算了列车荷载作用下的地铁隧道轨道结构中，钢轨、道床板、衬砌的总功率流，揭示了地铁隧道轨道结构振动能量的传递特性，得到如下主要结论：

1)振动能量从钢轨自上而下传递，经过道床板最后达到衬砌，因为引入了扣件和减振装置，所以功率流的传递特性受到了影响，在中频和高频，振动能量传递较少，主要集中在钢轨，而到了低频，道床板和衬砌结构受到影响较大，能量主要聚集在此。扣件在功率流从钢轨传递向道床板的过程中起到了显著的作用，改变扣件的刚度可以发现，钢轨向道床板传递振动能量的过程中，扣件衰减了这一作用，使得输入道床板的功率流得到减小，有利于减轻下部环境的振动。同时扣件也吸收了一部分的系统振动能量。扣件主要起作用的频率范围是中高频，对钢轨的影响比较显著。

2)扣件阻尼与钢轨、道床板和衬砌的功率流峰值有着密不可分的关系，除此之外，钢轨、道床板和衬砌的功率流出现峰值的数量也受到了一定程度的影响。加大扣件阻尼，随之带来的影响是道床板和衬砌的功率流的峰值数量也得到了下降。