基于改进遗传算法的无功优化在节能降损方面的研究

周 帅，张红旗，包 曼

（内蒙古农业大学，内蒙古 呼和浩特010000）

0 引言

电力系统无功优化的目的是在控制好电压质量的前提下，最大限度地降低网络中的电能消耗，通过减小网损以实现节约能源的经济目标。无功优化是降低电力系统有功损耗、提高电压质量、提高电网经济运行的一种有效手段。本文选择遗传算法作为无功优化工具，将传统遗传算法与非线性规划法相结合，既可以充分发挥遗传算法全局搜索能力较强的优势，也可充分体现非线性规划法局部搜索能力较强的特点。二者结合，可以弥补遗传算法容易陷入局部最优解的缺陷，提高算法的搜索能力，进而达到在无功优化中节能降损的目的。

1 无功优化数学模型

1.1 目标函数

本文采用罚函数对系统无功补偿容量QCi和发电机机端电压UGi进行约束，在保证系统电压质量的前提下，取得系统有功网损最小为目标函数。其数学表达式如下。

式中，ΔPs为系统有功网损；n为总支路数；Gij为支路i-j的电纳；Bij为支路i、j的电导；θij为节点i、j的相角差。

1.2 约束条件

1.2.1 等式约束条件

等式约束条件由电力系统有功平衡方程和无功平衡方程组成[1]。

式中，PGi为发电机发出的有功功率；PLi为用户需要的有功功率；Ui为节点i的电压；Uj为节点j的电压；QGi为发电机发出的无功功率；QLi为用户消耗的无功功率；QCi为无功补偿装置补偿的无功功率。

1.2.2 不等式约束条件

不等式约束即电力系统中的变量约束，由控制变量约束和状态变量约束构成。本文中选择可调变压器分接头位置TKi、无功补偿容量QCi和发电机机端电压UGi为控制变量，发电机的负荷节点电压UDi和无功出力QGi为状态变量。

控制变量约束表达式如下。

状态变量约束表达式如下。

罚函数设置如下

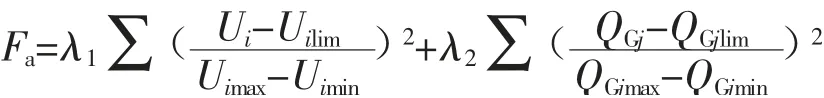
QGjlim为QGj的上限或者下限，规定如下。

2 改进遗传算法

2.1 编码方式

本文采用实数编码方式[2]，与传统二进制编码方式相比，实数编码方式的编码串很短，减小了优化过程中的计算量，提高了算法的运行效率。二进制编码方式在编码串较短的时候精度差，在编码串较长的时候过度占用空间，严重影响算法的寻优效率，实数编码则有效克服了二进制编码中编码串长的缺陷。

2.2 选择操作

本文选择轮盘赌方法进行操作[3]。基本原理是：每个个体被选中的概率与其适应度大小成正比。这种选择方法比较简单，容易实现。

2.3 交叉操作

本文采用改进单点交叉[4]方法进行操作，即2个个体基因差别较大时，以较好个体的基因为基准，接受较好个体的优良基因，使整个种群的进化向着最优解的方向靠拢。

2.4 变异操作

本文采用均匀变异方式进行操作[5]，其优势在于维持种群多样性的能力较强，在改善遗传算法局部寻优能力的同时，有利于求解多约束条件、多目标函数的问题。

2.5 优秀个体保存法[6]

在遗传算法优化过程中，定义每代适应度值最大的个体为优秀个体。本文在遗传操作之前先将当代的优秀个体保留，然后再将其他个体进行选择、交叉、变异操作产生新的种群，防止在遗传操作过程中破坏或丢失优秀个体的优良特性，使算法能够更好地收敛。

2.6 收敛准则

本文采用最大遗传代数与当前最优解经过多次迭代没有发生变化的原则[7]作为遗传算法的收敛准则，既可以解决在最大遗传代数之内寻得全局最优解还未输出结果的问题，又可以防止系统无限制运行的问题。

2.7 引入非线性规划函数

针对遗传算法的局部寻优能力较差，易发生“早熟”的问题，本文引入了非线性规划函数fmincon[8]，改善算法的局部搜索能力，提高算法跳出“早熟”的能力。设置在算法优化过程中，每进化10代，以所得值为初始值进行非线性化寻优。

3 算例与仿真

3.1 测试系统与算法

本文以电气和电子工程师协会IEEE（Institute of Electrical and Electronics Engineers）14节 点系统及30节点系统为测试系统，利用矩阵实验室MATLAB（matrix laboratory）平台，用简单遗传算法和改进遗传算法分别对测试系统进行优化仿真，将优化结果进行对比分析，验证算法改进的有效性。

3.2 IEEE14节点算例

EEE14节点系统中有5台发电机，其节点编号分别为1、2、3、6、8；有3台可调变压器，其首末端支路编号分别为5-6、4-7、4-9；还有1个无功补偿节点9。取平衡节点为节点1，PV节点为节点2、3、6、8，其余为PQ节点。设系统基准容量为100 MVA的标幺值，初始种群大小为100，系统最大迭代次数为50代。发电机节点电压的上限均为1.1（基准电压为每个电压等级平均额定电压的标幺值），下限均为0.9；其余节点电压的上限均为1.05，下限均为0.95。

表1给出了系统的优化结果。由表1可以看出，有功网损由优化前的13.63 MW降低至12.73 MW，即改进遗传算法能有效降低系统网损，表明算法的有效性。

表1 IEEE14节点算例优化对比（有名值）表

图1为IEEE14节点网损优化对比图。从图1可以看出，改进算法的收敛速度与简单遗传算法的收敛速度相比较快，一定程度上提高了算法的局部寻优能力，即改进遗传算法的收敛能力优于简单遗传算法的收敛能力。

图1 IEEE14节点网损优化对比图

3.3 IEEE30节点算例

IEEE30节点系统中有6台发电机，其节点编号分别为1、2、5、8、11、13；有4台可调变压器，其首末端支路编号分别为4-12、6-9、6-10、27-28；还有2个无功补偿节点，其节点编号分别为10、24。取平衡节点为节点1，PV节点为节点2、5、8、11、13，其余为PQ节点。设系统基准容量为100 MVA的标幺值，初始种群大小为100，系统最大迭代次数为50代。PV节点电压的上限均为1.1（基准电压为每个电压等级平均额定电压的标幺值），下限均为0.95；其余节点电压的上限均为1.05，下限均为0.95。

表2给出了系统的优化结果。由表2可知，有功网损由优化前的6.73 MW降低至4.52 MW，即改进遗传算法能有效降低系统网损，表明算法的有效性。

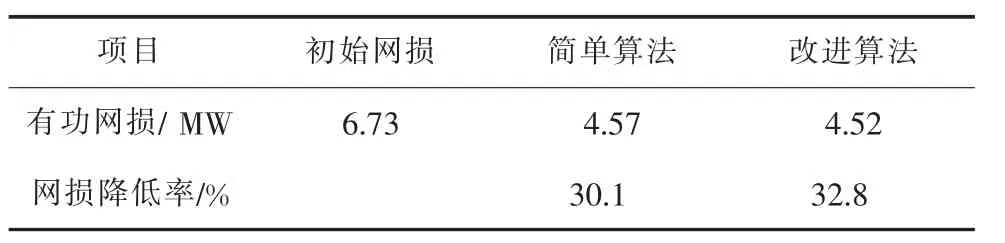
表2 IEEE30节点算例优化对比（有名值）表

图2为IEEE30节点网损优化对比图。从图2可以看出，改进算法的收敛性能明显优于简单算法，很好地解决了遗传算法局部寻优能力较差的问题。

图2 IEEE30节点网损优化对比图

4 结论

由IEEE14节点系统与IEEE30节点系统优化结果对比分析可以得出：在保证系统电压稳定的前提下，虽然改进遗传算法与简单遗传算法都能取得最优解，但是改进遗传算法的收敛速度明显快于简单遗传算法的收敛速度，同时改进遗传算法降低系统网损的能力更强。这两个系统的无功优化结果表明，改进遗传算法可以提高遗传算法跳出局部最优解的能力，更好地降低系统的网损。