采用相对熵评价雷达相对系统误差估值

高 效， 敬 东， 陈 钢

(中国人民解放军93209部队， 北京 100085)

0 引言

雷达相对系统误差是指雷达在对目标进行测量时存在的相对于指定参照系的固定误差，包括雷达动态测量中的测向误差Δθ、测距误差Δρ、仰角误差Δα、雷达站址标定误差(Δx,Δy)和雷达组网应用中存在的坐标转换误差等[1-4]。在雷达组网观测中，动态目标的绝对位置多数情况下是不可知的，我们比较容易得到的是在同一时间段内不同雷达对同一飞行目标的离散观测值。而相对于网内其他雷达来说，总会有一部雷达的观测是精确的，此时可以以该雷达(命名为主站)的测量值作为对目标位置的真实描述，其他雷达(命名为次站)以此为参照，从而求得次站雷达相对于主站雷达的相对系统误差。

估计、消除单雷达测量中存在的系统误差有两种途径：设备校准和数据校准[1-3]。对于多雷达组网后的系统误差校准，情况就更为复杂。如何评价一组系统误差估值或某种数据校准方法的有效性，成为一个亟待解决的问题。

传统的系统误差估值有效性评价多采用“取点评价法”，就是将同一时刻，雷达测量位置点与目标在参照系中的位置点(这两个点又称为时间配准点)之间的直线距离作为基本评价依据[5]。为了提高评价的可信度，往往需要取多个时间配准点，将多个时间配准点修正前后距离的平均值[6-7]之比作为最终的系统误差估值有效性评价指标。这种方法原理上比较科学，但在工程实现上，由于雷达异步工作，“多个时间配准点”在原始测量中几乎不存在，虽然采用卡尔曼滤波等方法可以外推得到配准时刻的目标位置点，但外推过程又不可避免地引入了新的计算误差，因此取点评价法的可操作性和准确性不高。

我们针对传统方法从局部(单点)入手带来的问题与不足，引入信息论中相对熵的概念，通过选取典型航路(目标保持一定高度沿直线飞行)上的一组主、从雷达测量数据，整体比较次站观测航迹线系统误差修正前后与主站观测航迹线的相似性来评价系统误差估值的有效性以及修正效果。这样在提高准确性和可操作性的同时，简化了评价方法的复杂程度，方便了工程上的实现。

1 基于相对熵的系统误差估值有效性评价方法

在信息论中，相对熵用来衡量两个取值为正的函数的相似性，比如：X为一非空集合，f(x)和g(x)是X上的两个离散随机概率分布函数，则f(x)和g(x)之间的相对熵定义为

(1)

对于上式，可以推导[8]：两个完全相同的函数，它们的相对熵等于零；相对熵越大，两个函数的差异越大，反之，相对熵越小，两个函数的差异越小；另外相对熵是不对称的，即

KL(f(x)||g(x))≠KL(g(x)||f(x))

为了便于使用，香农等人提出了新的相对熵计算方法，即：

KL(g(x)||f(x))]

(2)

我们采用式(2)作为雷达相对系统误差估值有效性评价的基本依据，具体方法步骤如下：

步骤1：选取主、次站雷达对同一空中目标的一段同时段观测数据。“同时段”是指两部雷达观测数据首点和末点时间差均不大于1个雷达探测周期(一般为10 s或20 s)。在目标作处于直线运动状态时，每部雷达观测数据点数量一般不少于10点，否则，每部雷达观测数据点4～6点即可。这样做的目的是选取较短时间内的单雷达测量点集合，既能保证所选测量点即时反映目标当前整体航迹走势，又要兼顾单雷达航迹线参数估计过程中消除随机误差影响的最少样本数要求。

步骤2：对主站雷达原始观测数据(极坐标形式)进行坐标变换，得到对应的统一直角坐标数据{(Xtzi,Ytzi)，i=1,2,…,n}，n表示主站雷达观测数据总点数。

步骤3：分别对次站雷达原始观测数据、系统误差修正数据进行坐标变换，得到两组统一直角坐标{(Xtcj,Ytcj)，j=1,2,…,m}和{(Xtxj,Ytxj)，j=1,2,…,m}，m表示次站雷达观测数据总点数。此处次站雷达系统误差修正数据是指次站雷达原始观测数据按照次站系统误差估值(Δρ,Δθ,Δα,Δx,Δy)修正后的数据。

步骤4：在统一直角坐标系中，对于测量点数据{(xi,yi),i=1,2,…,p}，将X坐标作为自变量，Y坐标作为因变量，分别对主、次站雷达观测数据和次站雷达系统误差修正数据进行曲线拟合，得到相应的参数估计。曲线拟合方法可以采用最小二乘或切比雪夫曲线拟合法，为了防止过拟合，拟合多项式的项数一般取2或3即可[9]。本文采用加权直线航迹线参数迭代估计模型(详见下一节)，得到主站观测航迹线参数(kz,dz)(分别表示直线的斜率和截距)、次站观测航迹线参数(kc,dc)和次站修正航迹线参数(kx,dx)。

步骤5：计算次站观测航迹线与主站观测航迹线的相对熵JSc。相对熵越小，表明两条航迹线越相似，过程如下：

① 计算f(xi)和g(xi)。

f(xi)=kzxi+dz，g(xi)=kcxi+dc，

i=1,2,…，n+m

(3)

式中，xi∈{(Xtzi|i=1,2,…，n)∪(Xtcj|j=1,2,…，m)}，表示主站观测点与次站观测点横坐标的并集，n和m分别表示主、次站雷达的观测点数。

② 计算KL(f(x)||g(x))和KL(g(x)||f(x))。

(4)

(5)

③ 计算JSc。

(6)

步骤6：计算次站修正航迹线与主站观测航迹线的相对熵JSx。计算过程与步骤5类同。

步骤7：次站修正航迹线系统误差估值有效性指标V表示为

(7)

V∈[0,1]时，V越大，表示系统误差估值越有效，航迹修正效果越好。V<0时，表示系统误差估值不仅完全无效，反而加剧了主、次站雷达观测航迹的分裂程度。

2 加权直线航迹线参数迭代估计模型

某时间段内单雷达观测到典型航路上的某一飞行目标的总点数为n，所有测量点转换到统一直角坐标系后表示为{(xi,yi),i=1,2,…,n}。我们定义单一测量点(xi,yi)对目标航迹线参数估计的贡献率为该点的权值，记为vi。首先按照以下方法计算单一测量点的权值。

基于直线方程一般式：y-k0x-d0=0(k0为直线的斜率，d0为直线在Y轴上的截距)，测量点(xi,yi)到直线的垂直距离li表示为

(8)

用所有单雷达观测点{(xi,yi),i=1,2…,n}到该直线的垂直距离li的平方和最小作为条件构造直线，计算在此条件下的这条直线的最佳参数，即为不加权直线航迹线参数估计模型：

(9)

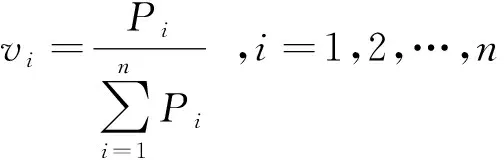
(10)

在测量点(xi,yi)对应的权值vi已知基础上，同样基于直线方程一般式，我们用所有单雷达观测点{(xi,yi),i=1,2,...,n}到某直线的垂直加权距离(vi×li)的平方和最小作为条件构造直线，计算在此条件下的这条直线的最佳参数(k,d)，即为单雷达加权直线航迹线参数估计模型[10]：

(11)

对于式(11)的求解，可以构造方程：

(12)

求解(12)式可以得到一组合理的直线参数解(k,d)。然后计算所有测量点(xi,yi)到新直线的加权距离之和fm(k,d)(m表示迭代次数)：

(13)

直到fm(k,d)不再减小为止，此时的(k,d)即为最佳直线参数；否则按照当前(k,d)重新计算所有测量点(xi,yi)的权值vi，回归对式(10)的求解过程。

3 方法应用与分析

使用本文方法，我们对某雷达网中一部次站雷达相对主站雷达的两种相对系统误差估值方案的有效性进行评价。

对图1中的次雷达原始测量航迹线、次雷达修正航迹线1、次雷达修正航迹线2相对于主雷达测量航迹线的相对熵分别进行了计算，计算结果如下：

图1 主、次雷达测量数据和两组次雷达相对系统误差修正数据显示图

主雷达与次雷达原始测量航迹线的相对熵JSc=0.188 534，主雷达原始测量与次雷达修正航迹线1的相对熵JS2x=0.002 087，主雷达原始测量与次雷达修正航迹线2的相对熵JS2x=0.084 058。则次站两组相对系统误差估值有效性指标V1和V2计算结果分别为

(14)

由1>V1>V2>0可以得出以下结论：

①V1和V2对应的系统误差估值均能有效减小主、次站雷达观测航迹的分裂程度,说明次站雷达的两组相对系统误差估值方案都有效；

② 在减小主、次站雷达观测航迹的分裂程度上，V1对应的系统误差估值要优于V2对应的系统误差估值，取得了较好的航迹修正效果,与图1的观察结果一致。

为了进一步验证本文方法在工程上的有效性，我们将图1中的主、次站雷达测量数据和次站雷达相对系统误差修正数据加入正态随机误差，连续进行了50次模拟，次站两组相对系统误差估值方案有效性指标V1和V2计算结果如图2所示，均有1>V1>V2>0的一致性结论，表明本方法有效，且受随机误差影响很小，可以应用于实际系统中。

图2 次站雷达相对系统误差估值有效性指标对比图

4 结束语

本文通过计算次站观测航迹线系统误差修正前后与主站观测航迹线的相对熵，构建次站修正航迹线系统误差估值有效性指标，用以评价系统误差估值的有效性以及修正效果。在工程应用中，很容易得到典型航路上的主、次站观测数据，既降低了检飞成本，又可以保证加权直线航迹线参数迭代估计模型的适用性，进而提高本评价方法的准确性。本方法有助于提高雷达阵地检飞、数据校准方法选择和雷达相对系统误差估值表计算过程中对系统误差估值评价的科学性、准确性和可操作性，从而提升雷达网目标状态估计和多雷达数据融合的质量。本文给出的方法，对研究基于位置信息以及目标空间运动特征的航迹关联算法也具有一定的借鉴意义。