四维盒子的展开图
2020-09-10

能够从特殊的情况推广出一个通用的原则,是相当不容易的一件事,它需要一些洞察力、想象力和发散思维能力,尤其在抽象的问题上,当凭直觉解题开始显得吃力的时候,这种推而广之的方式可能会打开从显见通往深奥的道路,比如,这个四维盒子的展开图。
大家都见过被拆开压平的纸箱,从一个三维的立方体变成了一串连在一起的二维正方形,那么,四维的盒子拆开以后,我们就能在三维的空间中看到它,
我们来做个推而广之的实验,从日常生活中人人都看得见的三维盒子开始,要得到一个立方体,需要六个面,这六个面是什么关系呢?
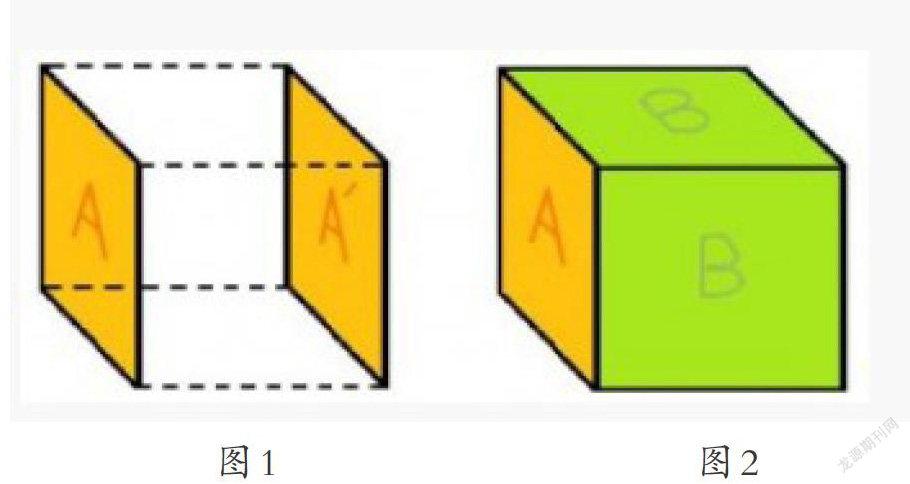
我们观察一个正方形,把它叫做“A”,A是一个二维的物体,它沿着第三维平移到A’处,它所经过的就是一个三维的空间,把这个空间封闭起来,就成了一个盒子,那么需要封闭几个面呢?观察上面图1.我们可以发现,因为A和A’两条相互平行的边之间需要一个面来封(叫做“B”),A有四条边,所以一共需要四个B,一个起始面,一个截止面,四个封闭面,这就是一个立方体。
把标注过的三维盒子拆开,我们可以见到这样的平面图:起始的A各条边都和一个B相连,截止的A’“挂”在这个对称图形的任意一个B上。
三维物体是用二维物体封闭起一段空间,那么四维物体就是用三维物体来封闭四维空间,所以四维盒子的各个“面”应该是立方体,剩下的问题是,需要几个立方体?怎样组合?
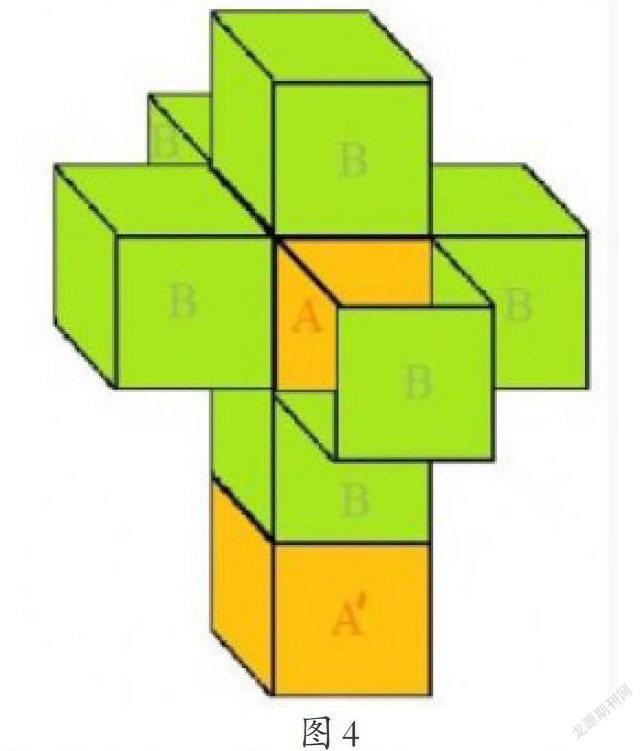
如果在假想的第四维上平移,我们需要一个起始立方体A,一個截止立方体A’,以及若干用于封闭的立方体B,在A和A’两个相互平行的面之间需要一个B,A有六个面,所以总共要六个B,看看上面的盒子展开图3.四维盒子就不难拆开了:一个A在中央,各面粘上一个B,在这个对称物体的任意一个B上粘个A’即可!
怎么样,和你想的一样吗?整个思路并不复杂,就像三维盒子可以有不同形式的展开图,这个答案不是唯一的,其它的情况对想象力的要求更高,你有兴趣做个不同的展开图吗?
