三十六个军官问题与欧拉方阵

相传18世纪时，普鲁士国王腓特烈大帝要举行一次盛大的阅兵典礼.当时腓特烈的军队有6个兵种，每个兵种又有6个军阶.腓特烈大帝命令他的阅兵司令：在每一个兵种、每一个军阶中各挑选一名军官组成一个6行6列的36人方阵，使每一行、每一列中都有各兵种、各军阶的代表，既不准重复，也不能遗漏.这件事情看起来很好办，不料命令传达下去之后，根本无法执行.阅兵司令接二连三地吹哨子，喊口令，排来排去，始终不能达到国王的要求.事后，国王对这件事情始终耿耿于怀，于是他就去请教当时欧洲一流的大数学家欧拉，希望欧拉能帮忙找到一个解决方案。

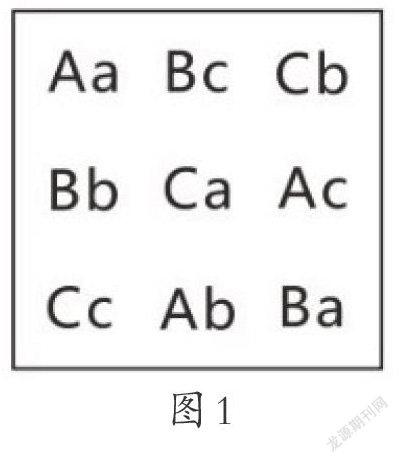
欧拉先从最简单问题人手，排出一个当n=3（即有3个兵种、3个级别时的方阵，用A、B、C表示不同兵种，用a、b、c表示不同级别的军官，如图1所示.这个方阵的每行每列中A、B、c各有一个，a、b、c也各有—个，并且没有遗漏和重复

然后，欧拉又排出了n=4、n=5的方阵，它们均满足条件且都不重复，所以这样的方阵就被称为欧拉方阵。

可是对于n=6（即6个兵种，6个不同级别的军官）的方阵，欧拉绞尽脑汁也没有排出来.因为6是能被2整除而不能被4整除的数，欧拉称它们为半偶数.于是欧拉猜想，由半偶数组成的方阵不存在.1782年欧拉在谈论这个问题时说：“我已经试验研究了很多次，我确信不可能作出两个六阶的，并且对于10、14，……以及奇数2倍的阶数都是不可能的.”欧拉认为：4n+2阶的欧拉方阵是不存在的，这个结论被后人称之为“欧拉方阵猜想”。

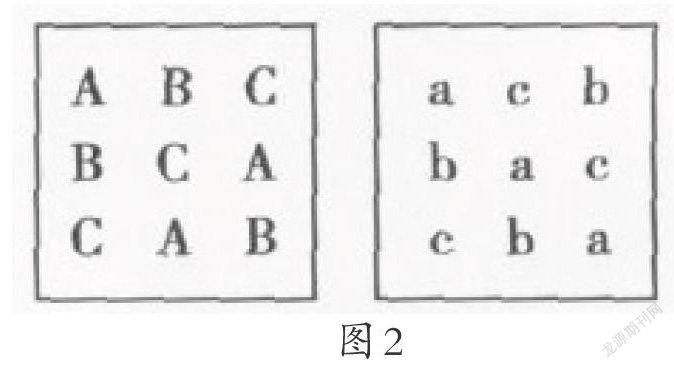
歐拉的关注引起了全世界数学家对这个难题的重视，为了研究方便，他们把上面的一个方阵拆分成两个方阵来表示，这种由字母构成的方阵称为拉丁方阵（图2）.若左右两个拉丁方阵能叠合成一个欧拉方阵（如图1），则称这两个拉丁方阵是互为正交的.若能证明n是半偶数时，不存在正交的拉丁方阵，就相当于证明欧拉的猜想是正确的。

由于构造正交拉丁方阵非常困难，数学家们对欧拉方阵猜想的研究进展也很慢.直到1910年，法国数学家加斯顿·塔里在他的兄弟赫伯特.塔里的帮助下，列出了全部的六阶拉丁方阵，验证了它们当中任意两个都是不正交的，从而证实了n=6时欧拉猜想是正确的.但塔里兄弟没有从理论上加以证明，这是一个很大的缺陷，而且随着阶数增大，列出全部拉丁方阵的方法也不可取，即使列出全部拉丁方阵，要验证每两个是否正交就更加困难。

1959年4月，印度数学家玻色和斯里克汉德构造了两个22阶正交拉丁方阵，从而否定了“欧拉方阵猜想”.不久后，他们又证明：除n=2、6、14、26外，n阶欧拉方阵都是存在的.接着，美国数学家帕克又构造出了14阶与26阶的欧拉方阵，至此，欧拉方阵猜想只对n=2、6成立，其余都是错的.这个否定的结果是人们在180年的努力中未曾想到的。

类似这样的方阵，在工农业生产和科学实验领域都有极其广泛的应用，利用它能以较少的实验次数获得较好的结果，还能节省原料、改进配方等。