基于帧间匹配去噪的角接焊缝识别

谢盛 魏昕 梁梓铭

摘要：焊接图像存在着大量的噪声干扰，对其进行处理是焊缝识别的前提。针对被动视觉焊缝跟踪系统的图像去噪问题，提出了基于帧间匹配的去噪方法，通过将旋转不变性二进制描述算法（Oriented FAST and Rotated BRIEF，ORB）与随机采样一致性算法（Random Sample Consensus，RANSAC）相结合，得到两帧图像间的单应矩阵，并以此对齐两帧图像内的焊件，采用帧间图像灰度替换的方式，用焊件图像替换飞溅区域得到无飞溅的焊缝图像。针对角接焊中焊件边缘直线的干扰，对比了最小二乘法、霍夫变换、RANSAC三种直线拟合算法，结果表明RANSAC算法在大量错误数据的干扰下拟合精度可达2个像素，满足焊缝跟踪的需求。

关键词：焊缝跟踪;被动视觉;角接焊缝;特征匹配;直线拟合

0 前言

基于视觉传感器的焊缝识别技术因其方便直观且信息量大成为研究热点，相对于主动视觉，被动视觉传感器具有结构简单、成本低等优势，但由于被动视觉采用自然光源照明，焊接过程中的强光和飞溅等会给焊缝图像引入大量的噪声干扰，如何去除噪声是实现焊缝跟踪的首要问题。目前工程上通常采取两种方式处理：增大激光传感器的前视距离或加遮挡板，或改善图像处理软件算法[1]。在图像处理算法方面，Wu等[2]对比了高斯滤波器、中值滤波器和维纳滤波器在焊缝图像处理中的效果，验证了中值滤波可以有效去除焊缝图像中随机出现的椒盐噪声。Zou等[3]根據帧间图像连续性，提出了一种具有强大的特征表达能力和深度卷积神经网络的自学习功能图像处理算法，可从含有大量噪声的图像中检测焊缝位置。W.P.Gu等[4]在激光结构光视觉图像处理中，利用线激光宽度小于12像素，而飞溅、弧光等干扰宽度大于16像素的特性将干扰去除，但该方法有几率会将焊缝区域一起去除。Fan等[5]采用两帧图像之间的“最小操作”进行飞溅的去除。Li 等[6]通过设置动态ROI区域降低飞溅造成的干扰。文中以激光焊接中被动视觉传感器采集到的角接焊焊缝图像为例，详细介绍了基于帧间匹配的去噪方法流程，同时，对比了最小二乘法、霍夫变换、RANSAC三种算法在有大量错误数据存在时的焊缝拟合效果。

1 基于帧间匹配的去噪方法

针对窄间隙角接板外部激光焊接，焊缝图像采集系统采用被动视觉传感器，相机固定于激光焊枪正前方，焊枪轴线垂直于焊件，焊接方向至左向右，焊接过程中采集的连续两帧图像如图1所示。由于拍摄有一定时间间隔，图像中飞溅的位置区别较大，因此可以通过对比图像之间像素灰度值将飞溅去除，但由于相机产生了运动，直接进行灰度替换会导致像素区域不匹配，不仅会破坏原有焊缝细，还会引入不必要的干扰。采用ORB（Oriented FAST and Rotated BRIEF）和RANSAC（Random Sample Cons-ensus）结合得到图像间的变换矩阵，将第一帧图像变换到与第二帧图像对齐后再进行像素操作，可以在不损失细节的情况下去除大量飞溅噪声，再配合中值滤波可以得到很好的去噪效果。

ORB基于oFAST特征检测和rBRIEF的特征描述子，具有一定的尺度不变性、旋转不变性和抗噪性，速度比常见的SIFT算法快两个数量级[7]。通过ORB粗匹配后会有大量的误匹配出现，常用的方法是采用RANSAC算法进行匹配点筛选，并计算出单应矩阵。

1.1 oFAST特征检测

图像的特征点即为图像中较为明显的点。在焊缝图像中，焊缝边界点、工件表面的污点、工件边缘的边界点、飞溅处的亮点、暗处的黑点均可成为特征点。FAST检测原理[8]是：在图像中取一个像素点P，像素值记为Ip，以r为半径画圆，判断圆上的像素点是否连续n个大于Ip加上阈值t，或者连续n个小于Ip减去阈值t，若有则该像素点可能为角点。FAST角点检测原理如图2所示。

为了减少角点数量，排除不稳定角点，采用非极大值抑制进行筛选，对每个角点计算响应得分，以当前特征点为中心，判断其在给定邻域内是否为最大响应得分，若是则保留，不是则抑制。强度响应函数为：

采用灰度质心法为FAST算法提取的角点添加方向属性，以角点p为圆心，半径r范围内的点计算出灰度质心C，p与C的连线方向记为角点的方向。

为了使特征具有一定的尺度不变性，运用图像金字塔，在每层图像提取FAST特征，为特征点引入尺度属性σ，并称之为oFAST。

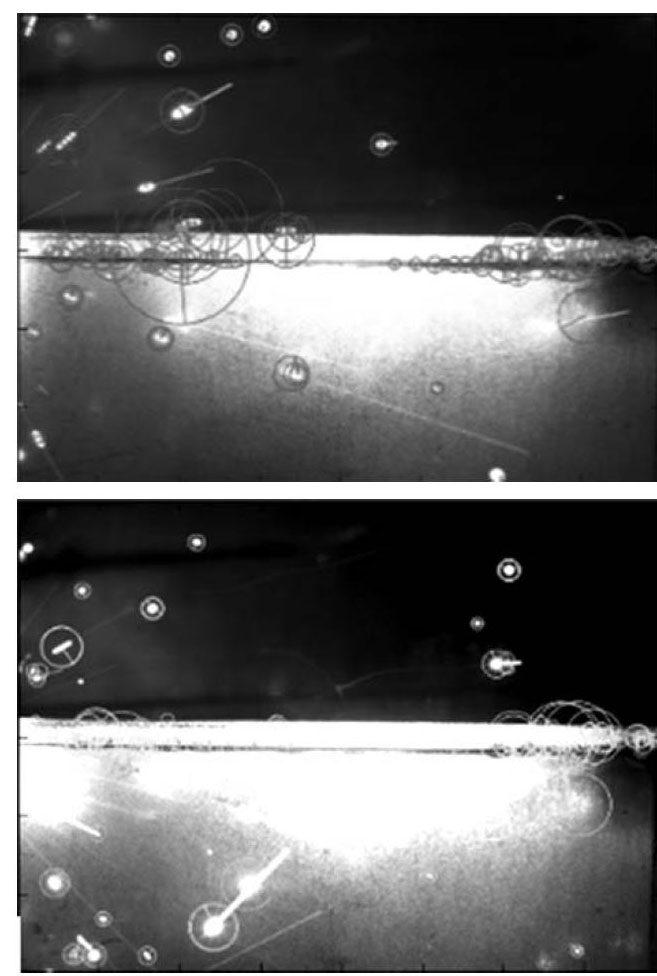
检测到的FAST角点及其方向如图 3所示，其中圆心为特征点坐标，从圆心连接到圆上的线段方向为特征点的方向，圆的半径为特征点的尺度，可以观察到图像中样件上的表面细节、焊缝位置的纹理和飞溅均被检测到作为特征点。

1.2 rBRIEF特征点描述子

BRIEF描述子采用二进制码串作为描述子向量，相对于SIFT和SURF描述子，在内存占用及计算耗时等方面均占优势，但是BRIEF描述子不具有旋转不变性，ORB算法中对BRIEF进行了改进，在计算描述子的过程中引入了特征点的方向，并称之为rBRIEF。由于BRIEF算法易受噪声影响，首先对图像进行高斯平滑处理。具体流程如下[9]：

在平滑处理后的图像中，以特征点p为中心，取范围为31×31的窗口，在窗口内根据高斯分布随机选取n对子窗口，范围为5×5，分别比较每对子窗口的灰度积分值，可定义一个二进制检测τ：

1.3 特征点粗匹配

通过ORB算法得到两帧图像中的特征点描述子后，采用BruteForce匹配算法，根据两帧图像特征点描述子之间的Hamming距离判断该特征点是否匹配，当汉明距离小于阈值T时，即认为两个特征匹配，保留匹配点对，反之则去除匹配点对。但此时的匹配还存在大量的误匹配点，无法以此正确计算出两帧图像间的变换矩阵。

1.4 RANSAC特征点筛选

为了得到两帧图像间的最佳变换矩阵H，选择经典的RANSAC算法进行特征点筛选。RANSAC算法采用迭代的方式，从一组包含离群的被观测数据中估算出数学模型的参数，在图像匹配中常用于消除误匹配，RANSAC算法需要用到单应矩阵H（Homography Matrix）。单应矩阵H可以用于描述两帧图像间的映射关系，包括平移、旋转和缩放，可定义如下：

其中（x，y）为第一帧图像的粗配准得到的特征点位置，（x'，y'）为第一帧图像的特征点位置。RANSAC算法基本流程为[10]：

（1）通过两帧图像粗匹配得到N个待匹配点集，并分别进行坐标归一化。

（2）由于单应矩阵有8个参数，每个点对可以列2个方程，所以需要从N个点里随机选取4个不共线的点对，并解出H的8个参数。

（3）将第一帧图像中余下的N-4个点对根据H进行变换，根据变换后的结果计算两帧图像特征点间的欧式距离d=‖HA-A'‖，如果小于设定的阈值t，则将该点对归为内点。

（4）重复执行步骤（2）和步骤（3）2 000次，记录每次的内点数量。

（5）选择内点数量最多的内点集合，以该集合对应的为最优匹配值。

通过以上步骤可以求得第一帧到第二帧的单应矩阵H。第一帧图像到第二帧图像的精匹配结果如图 4所示，可以看出误匹配点均被去除。

1.5 帧间替换去噪

通过第一帧到第二帧的单应矩阵H，可以将第一帧图像P1中的样件与第二帧图像P2中的样件对齐，即对第一帧图像中的像素点进行变换：Ai'=HAi，令变换后的第一帧图像记为P1'，需要注意的是：P1'中有部分区域灰度值是为0的，在替换过程中需要进行筛选。已知焊接过程中拍摄到的飞溅区域灰度值在240以上，且在两帧图像中大多数飞溅位置不同，令替换后的图像为P2'，像素坐标为（x，y），P1'（x，y）为（x，y）点的灰度值，那么可以通过以下逻辑将飞溅去除：

（1）如果5<P1'（x，y）<240且P1'（x，y）<P2（x，y），则将P1'（x，y）赋值给P2'（x，y）。

（2）其他情况则将P2（x，y）赋值给P2'（x，y）。

通过以上步骤可以得到去除飞溅后的第二帧图片，如图5所示，图像中的大部分飞溅已被去除，且保留了大多数细节。文中的图像处理在ubuntu16.04上完成，CPU为i5-10210u 1.6 GHz，内存16G，图像大小为600×800，帧间匹配去噪算法平均耗时为26 ms。

2 焊缝直线拟合

去除飞溅后的图像经过中值滤波、自适应阈值分割、形态学处理后得到如图6所示的二值化焊缝图像，由于是角接的方式外部焊接，二值化后的图像中有焊缝及竖直板外侧面边缘两条较明显直线，若要去除外侧边缘的影响势必会损失焊缝特征。分别采用最小二乘法、霍夫变换、RANSAC法三种方法进行焊缝拟合实验。

2.1 最小二乘法

最小二乘法常用于焊缝直线的拟合，原理是[11]：给定数据点集C={（x1，y1），（x2，y2），…，（xn，yn）}，并给出直线函数原型：

求出a、b后便可得到拟合直线。将二值图像中的白色像素点取出组成数据点集，采用最小二乘法进行直线拟合，算法平均耗时0.006 ms，结果如图7所示，图7a为数据点集的拟合效果，图7b为与实际焊缝位置的对比。由拟合结果可见，最小二乘法对全部數据点都进行了拟合，所以无法排除焊接样件侧边缘的干扰，拟合的位置也向两直线中间偏离，不适用于此类焊缝的拟合。

2.2 Hough变换

Hough变换是一种常用的直线拟合算法，具有良好的抗噪性能。直线的极坐标方程为：

式中 ρ为原点到直线的距离;θ确定直线的方向。图像中的每一条直线都可以与一对参数（ρ，θ）对应，这个参数平面称为霍夫空间。图像中每条直线对应霍夫空间一个点，每个点对应霍夫空间一条正弦曲线。在θ取值为（-90°，90°]内，并以θ和ρ的间隔划分霍夫空间，给每个划分的区域设置累加器H（ρ，θ），将图像中的所有像素点映射到参数空间中[12]，累加到对应的H（ρ，θ），当H（ρ，θ）的值大于所设阈值时则认为直线存在，直线方程为：

选取H（ρ，θ）值最大的一条直线作为最终拟合的焊缝直线，效果如图8所示。经过多次实验发现，处理θ轴分辨率设为1°时，算法平均耗时为3.3 ms，霍夫变换依旧存在错检的情况，且多次出现平均误差大于10个像素的情况。

2.3 RANSAC直线拟合

RANSAC广泛应用于已知模型的参数估计问题，对于处理存在野值点的数据十分有效，而直线估计是其最简单的应用，基本原理如下：给定数据点集，在其中随机选取两个点，以此两点得到一条直线，算出点集中剩余点到该直线的距离，将距离小于设定距离阈值的点归为内点，重复若干次随机选点，得到若干条直线及相应的内点集合，从中选择内点数量最多的集合，用最小二乘法拟合此集合内的所有内点即可得到直线。

将迭代次数设置为2 000次，RANSAC直线拟合效果如图 10所示。经过多次实验对比Hough变换和RANSAC算法，发现RANSAC算法精度均高于Hough变换，均在 2个像素以内，即0.21 mm内，且在错误数据干扰强弱变化下均有很好的稳定性，RANSAC算法平均耗时高于Hough变换，约为8.5 ms。

3 结论

（1）针对被动视觉的焊缝识别图像中的飞溅干扰，提出了基于帧间匹配替换的去噪方法，有效地去除了焊接过程中图像中的飞溅干扰，并且保留完整的焊缝细节，为后续的焊缝提取、焊缝表面形貌观察、在线检测等工作提供了便利。

（2）针对角接焊的焊缝图像中出现焊件侧边缘直线干扰情况，分别采用三种不同的直线拟合算法进行焊缝拟合实验，结果表明标准最小二乘法不适用于此类焊缝的提取，Hough变换易受到错误数据的影响，且精度低于10个像素，RANSAC算法稳定性优于Hough变换，精度为2个像素，RANSAC算法更适合于此类焊缝的拟合。

参考文献：

[1] 陈华斌，孔萌，吕娜，等. 视觉传感技术在机器人智能化焊接中的研究现状[J]. 电焊机，2017，47（3）：1-16.

[2] Wu Q，Lee J，Park M，et al. A Study on Development ofOptimal Noise Filter Algorithm for Laser Vision System in GMA Welding[J]. Procedia Engineering，2014（97）：819- 827.

[3] Zou Y，Zhou W. Automatic seam detection and trackingsystem for robots based on laser vision[J]. Mechatronics，2019（63）：102261.

[4] Gu W，P X Z. Autonomous seam acquisition and trackingsystem for multi-pass welding based on vision sensor[J].Int. J. Adv. Manuf. Technol.，2013（69）：451-460.

[5] Fan J，Jing F，Yang L，et al. A precise seam tracking met-hod for narrow butt seams based on structured light visionsensor[J]. Optics & Laser Technology，2019（109）：616-626.

[6] Li X，Li X，Khyam M O，et al. Robust Welding Seam Tra- cking and Recognition[J]. IEEE Sensors Journal，2017，17（17）：5609-5617.

[7] Rublee E，Rabaud V，Konolige K，et al. ORB：An efficientalternative to SIFT or SURF：2011 International Conferenceon Computer Vision，2011[C]. IEEE，2011.

[8] Rosten E，Drummond T. Machine Learning for High-SpeedCorner Detection[M]. Berlin，Heidelberg：Springer Berlin Heidelberg，2006：430-443.

[9] Calonder M，Lepetit V，Ozuysal M，et al. BRIEF：Computinga Local Binary Descriptor Very Fast[J]. IEEE Transactionson Pattern Analysis and Machine Intelligence，2012，34（7）：1281-1298.

[10] Raguram R，Frahm J，Pollefeys M. Exploiting uncertaintyin random sample consensus，2009[C]. IEEE，2009.

[11] Markovsky I，Van Huffel S. Overview of total least-squaresmethods[J]. Signal Processing，2007，87（10）：2283-2302.

[12] 鄧景煜，王玉华，易俊兰，等. 焊缝图像多分辨率Hough变换分析[J]. 应用激光，2019，39（5）：847-851.