《绳法经》中的数学知识

李娇

《绳法经》如果按照意译，即为“结绳的规则”，它成书的具体时间已无法考证，据推测，它大约是在公元前8世纪到2世纪间陆续完成的，问世的时间比印度知名的史诗《摩诃婆罗多》和《罗摩衍那》还要早，《绳法经》是印度的数学文献，共有7本，先后由博德雅纳（Baydhayana）、阿帕斯坦巴（apastanba）和卡提亚讷（Katyavana）三个人编撰而成。

《繩法经》中记载的主要内容是祭坛的建造问题，作者利用绳子和竹杆给出了固定的测量法则，其中涉及的数学知识比较零碎，但足以说明在成书时印度数学家已取得了很出色的成就。

祭坛的建造必须按照一系列严格的指令来完成，在设计与建造的过程中，人们需要顾及朝向、地基的形状，所有祭坛的地基分为两大类，一类是面积成整数比的正方形，另一类则是等积的各种多边形，这需要运用到很多的几何作图知识，如直角、正方形、边长为整数的直角三角形、梯形等的作法;从面积为a的正方形出发，作面积为na的正方形;把直角三角形改为等积的正方形;等等，在这里，毕达哥拉斯定理得到了广泛的应用。

《绳法经》中详细介绍了用线绳和竹杆拉出直角的方法，并用到很多的边长为正整数的直角三角形及其相似形，如边长为3.4.5;5.12.13;8.15.17;7.24.25;12.35.37;15.36.39等直角三角形，以及与这些三角形等面积的梯形。

利用毕达哥拉斯定理可以由已知正方形作面积为其2倍、3倍以至n倍的正方形，并进一步作面积等于两个不等积正方形面积之和a+b的正方形，阿帕斯坦巴把作图法则叙述为：“拼合两个不等积正方形，在大正方形的边上截取等于小正方形边长的线段，经过此平面区域斜拉绳子，使两个正方形合在一起，”如图1.此处AB=a+b。

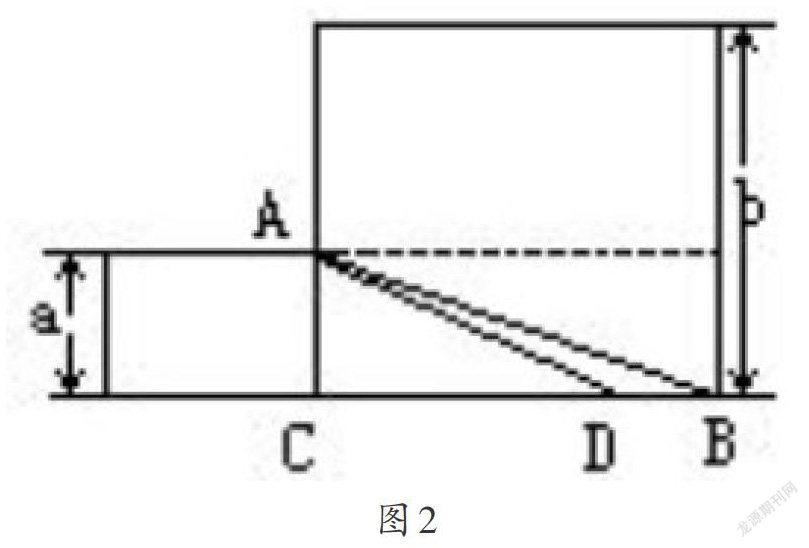
《绳法经》中还给出了求两个已知正方形面积之差的正方形面积问题及其解法，其解法是：以点A为中心，以大正方形边长为半径，在底边CB上截取线段CD，则CD=b-a（图2）

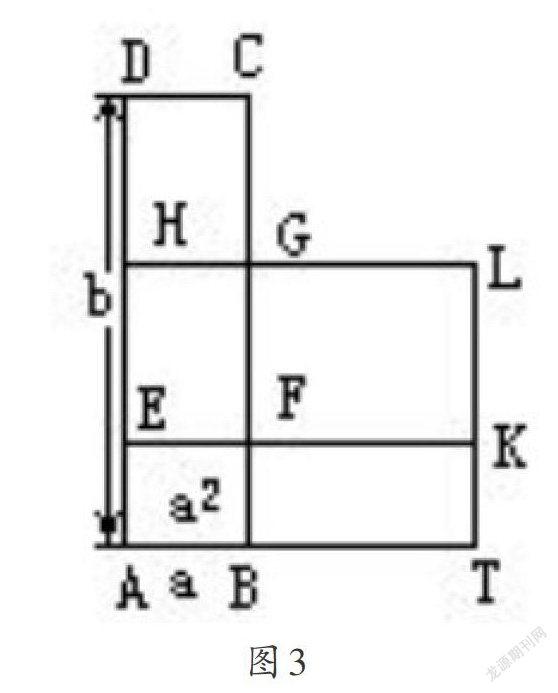
毕达哥拉斯定理还可用来把已知矩形改为等积的正方形，如图3.首先在边长AB=a，AD=b的矩形中分割出正方形ABFE，使其面积等于a;用直线HG平分余下的部分四边形EFCD;在BF上作矩形BIKF使其与矩形EFGH全等，则原矩形ABCD与磬折形AIKFGHA等积，它的面积等于两个已知的正方形AILH与FKLG的面积之差，这样就完成了作图。

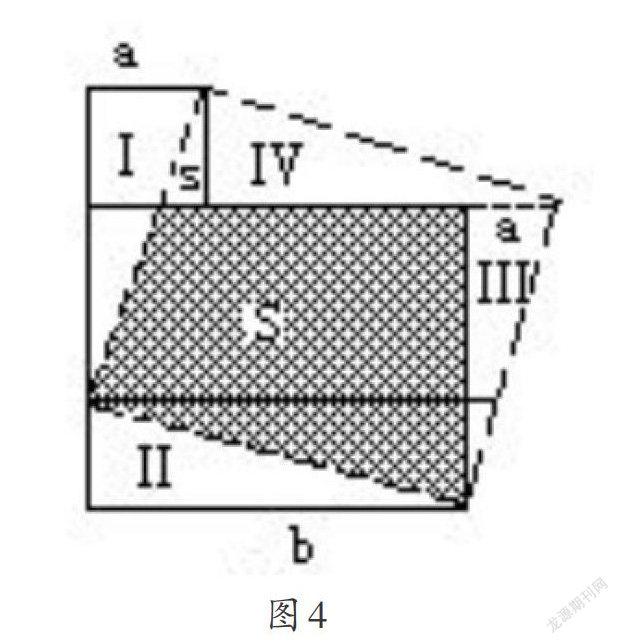
如果在图2中引进辅助线段，如图4所示，那么就能得到一个可以从直观上表示毕达哥拉斯定理的图形，以斜边的长为边长的正方形由s、Ⅲ、Ⅳ和s四部分组成，而三角形I、Ⅱ、Ⅲ、Ⅳ等积，由此可以推测，在作者撰写《绳法经》时，印度的数学家已经知道毕达哥拉斯定理的证明方法，但也有可能是，在发现了边长为整数的特殊情形后，才得到定理证明的一般方法，但是这也并不排除从其他民族那里得到这一结果的可能性，事实上，只要发现了倍正方形问题与古希腊倍立方体问题的相似性，就可以得出这个结论。

很多印度学者对边长为整数的直角三角形的作法产生了浓厚的兴趣，婆罗摩笈多和马哈维拉给出了一般的作法，在印度，边长为整数的直角三角形的作法始终与建筑学联系在一起。