一种DES和RSA的联合加密方法

杜志学

摘 要：信息高速发展的时期，信息安全越来越引起重视。对信息进行加密处理，无疑是提升信息安全的最佳手段。目前，对称加密体系和非对称加密体系都存在着各自的优缺点。文章通过对DES和RSA加密的研究分析，提出一种DES和RSA联合加密的方案。这种方案充分地利用了RSA加密安全性和DES加密快速性的优势，大大提升了信息安全。

关键词：DES;RSA;加密

中图分类号：TP309.7 文献标识码：A 文章编号：1674-1064（2020）08-0029-02

二十一世纪被誉为信息的世纪，伴随着科技的进步，互联网的迅猛发展，每时每刻都有数以亿计的信息在互联网上传输。身为倾听者和发送者的人们开始意识到，互联网给其带来无限便利的同时，也将其所有行为暴露给了不法之徒。信息在网络中传输的安全问题尤为凸显，如何提升信息在传输过程中的安全性、完整性，成为网络安全专家的重要职责。当下，提升信息传输安全的最有效途径就是使用加密技术。

1 密码学

信息安全领域最关键、最核心的技术就是密码学，加密技术和解密技术是其重要的构成部分。在密码学中，需要加密的信息被称为“明文”;某种特定的处理明文的过程被称为“加密”;加密后所得到的信息被称为“密文”;收到信息后，对信息的逆向处理，恢复明文的过程被称为“解密”;在加密、解密中使用到的参数被称为“密钥”。

在现代密码学理论建立过程中，最重要的时间节点为1976年《密码学新方向》一文的发布。该文中第一次提出可以在网络上实现的公钥密码理论，开启了公钥密码研究的时代[1]。

1.1 对称密钥体系

对称密钥加密技术是一种传统的加密技术，其原理是：发送者和接收者采用同一种加密规则，对明文和密文进行正运算和逆运算。因其采用相同的规则，即相同的密钥，所以把这种方法称为对称加密法。需要通信的双方必须在通信前通过安全的方式商议出一个保密的密钥，一旦密钥泄露出去，就可以被还原出所发送的原文。因此，密钥的保密程度决定了通信的安全，如图1所示。

在对称密码体系中一般分为：分组密码体系和流密码体系。其中，分组密码被较多使用。分组密码是先对需要加密的明文进行编码，编码后的明文数字按照特定的方式分成数据块（一个块称为一个分组），依次对每个组进行加密处理，并发送出去。

DES（数据加密算法）是最经典的对称加密算法，也是最广泛使用的加密算法，是分组加密的代表算法。其自1975年发布，很快就在非国防的其他各领域迅速地应用起来。DES加密的明文必须分组为64bit，密钥长度也是固定的64bit，但实际有效密钥仅为56bit。另外，8bit为密钥的校验位，即第8、16、24……64位。

DES（数据加密算法）主要步骤如下：

初始置换。先将输入的64位明文进行初始置换。置换后的明文只是原明文中的信息排列顺序有所改变，依然是64位的明文格式。再将置换后的明文分成前后两个部分和，表示前32位、表示后32位。

16轮迭代。这一步是加密的过程，此过程要重复16轮，每一轮的加密都是采取相同的加密算法。其操作通过两种可逆运算：混合和代换得到。

逆置换P -1。最后通过逆置换表得到密文。

DES加密的特点：

DES加密因其是对称密钥系统，必须在通信前协商密钥，这个过程就会造成本应是相互的私钥却要在开放的网络中传输。一旦在协商的过程中被窃取，即便为密文傳输，也会被窃取者解密出明文。

DES的密钥长度为固定的56位（带校验位为64位），二进制数非常短，很容易受到穷举攻击。当采用穷举攻击时，只需要进行次就可以破解出明文。而DES加密的密钥只有56位，即次。这个数字对于现阶段的计算机处理能力已经非常的轻松了。

DES的56位密钥虽然短，但是实现加密处理非常简单，加解密速度就非常快，适合于保密级别不高的密文传输。

1.2 非对称密钥体系

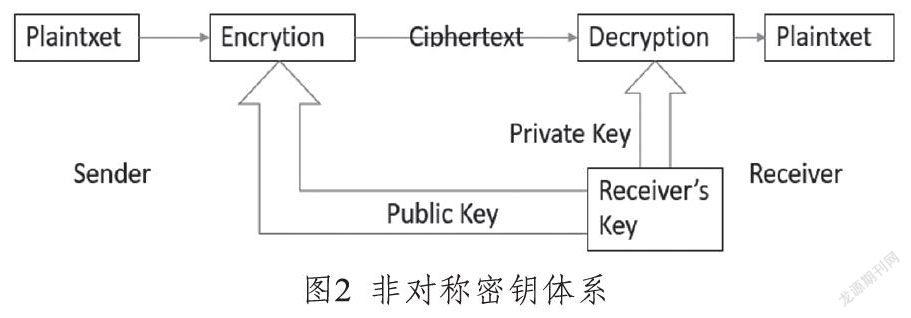
非对称密钥体系，又称为公钥加密体系。一被提出，就改变了人们对密码学原有的认知。使用具有某种对应联系的两个规则即可完成加密和解密的过程。同时，无需直接传输密钥，就可以完成解密的过程。其不再采用对称密钥体系的置换和替代的方法，而是通过基于数论中的函数来计算出公钥。自己保留解开密文的私钥，可以最好地确保密钥的安全性。其基本模式如下：

接收者依靠某种函数计算出公钥和私钥。将公钥发送给对方，命其使用公钥对发送的信息进行加密，私钥自己保密。

发送者在获取到公钥后，按照接收者的要求使用公钥对信息进行加密。

接收者在收到密文后，使用自己保留的私钥对密文进行解密。

由于私钥只有自己保留，只要不将私钥泄露，那所有的通信都将是安全可靠的，如图2所示。

RSA加密是最典型的非对称密钥加密方式，也是当前使用最广泛的非对称密钥加密方式。其由MIT的三位数学家所提出，众多的国际组织均支持RSA加密标准。PGP（电子邮件安全协议）也是依据RSA加密标准设计的。RSA加密之所以被广泛地接受，是因为其算法通过大数难以因式分解的数学函数原理，确保加密机制的安全可靠[2]。

RSA加密所涉及到数论的相关知识如下：

同余：当p是大于1的自然数，x是整数，的倍数，在数论中就写成。

互质：公约数只有1的两个整数。如2和3互质，在数论中就写成。

欧拉函数：

欧拉定理：整数，整数，且，那么 。

RSA算法密钥的生成过程：

找到两个素数：p和q，p和q需要保密，并且p和q越大安全性越高。

计算出p·q=n，利用欧拉函数得出：

。

寻找一个随机数e，使用<，且。（e，n）就是加密的公钥。。

计算，得出d。（d，n）就是解密的私钥。

RSA的加密、解密过程：

加密运算：使用明文m和公钥e进行运算，得出的c就是密文。

解密运算：使用密文c和私钥d进行运算，还原出明文m。

RSA加密的特点：

密钥传输方便。因其是非对称加密，只需要传输对明文加密所使用的公钥，通过公钥无法推断出解密所需的私钥。

密钥生成麻烦。因其密钥生成的原理，生成密钥的过程复杂，很难实现每次传输信息都可以更换密钥。

速度慢。目前的RSA的分组要2048bit长度的密钥。

1.3 DES和RSA联合加密算法

经过DES和RSA算法的研究发现，其各自都存在优缺点。进一步分析两种算法的优缺点，发现双方是可以互补的[3]。两种算法对比一下：DES加密的速度虽然快，但是在密钥的保护上存在安全性隐患。RSA是將公钥传给对方，自己保留私钥，无密钥保护的问题，但是其算法复杂加密速度较慢。

综合两种加密方式做一种联合加密方式，先使用DES对明文进行加密，再使用RSA对DES的密钥进行加密。这样既解决了DES安全性问题，又提升了RSA加密的速度，如图3所示。

2 结语

文章从对称加密体系和非对称加密体系的原理开始阐述，从数学基础开始，到加解密原理，再到加解密过程，分别对两种加密体系的典型加密方式（DES加密和RSA加密）进行分析。提出一种DES和RSA联合加密的方式，充分利用DES和RSA的各自长处，弥补彼此的不足。使信息在加解密数据的安全性和加密效率上得到了平衡。希望这种联合加密的方式在各种业务中推广使用。

参考文献

[1] James S.Tiller.A Technical Guide to IPSec Virtual Private Networks[J].Boca Raton.FL：CRC Press LLC，2001：3-6.

[2] 陈春玲，齐年强，余瀚.RSA算法的研究和改进[J].计算机技术与发展，2016，8（8）：48.

[3] 陈侨川.一种基于DES和RSA算法的混合加密算法[D].昆明：云南大学，2015.