基于接收信号强度的阵列校正与信号源DOA估计及定位
2020-09-10陈涛康乐峰王凯锐王新文张贺勇
陈涛 康乐峰 王凯锐 王新文 张贺勇


摘 要:阵列信号处理是信号处理的重要部分之一,为了提升阵列处理波达方向估计和波束性能,需要对其实施阵列校正。本次研究在模拟分析阵列接收信号基础上,实现关于阵列信号处理的波达方向(direction of arriving,DOA)估计和阵列误差校正研究。研究结果显示阵列误差对DOA估计中,如果是阵元增益误差下不会导致出现谱峰位置偏移,但是谱峰幅度会降低;如果出现阵元相位误差,同时也存在附加相位项的影响,会出现谱峰偏移;如果存在互耦误差,不但会对空间谱尖锐程度造成影响,也会影响谱峰位置,因此均需要实施分析和校正。本次研究基于综合DOA估计算法实现信号源的模拟仿真,取得了良好的估计结果。
关键词:接收信号强度;阵列校正;信号源DOA;估计
中图分类号:TN953.7;TN957.51 文献标识码:A 文章编号:1674-1064(2020)09-0020-04
阵列信号处理,是在空间中设置多个传感器,以实现对空间不同位置信号的检测;建构传感器阵列,在阵列应用下实现空间信号的接收和处理,主要是提取阵列信号及其特征信息,也可以实现对噪声或不感兴趣信息的抑制[1]。阵列信号处理方式和其他处理方式存在差异,主要是基于信号空域的特性强化信号,且将信号空域信息提取出来[2]。因此也可以将其称为空域信号处理,具有信号波束控制强、抗干扰能力和信号处理能力高等优点,因此引起了广泛的关注,也逐渐扩大了其应用范围[3]。超分辨波达方向估计(DOA)为阵列信号处理的内容之一,文章结合综合DOA估计算法实现信号源的模拟仿真分析,以实现阵列校正,并对信号源的DOA进行估计。
1 阵列接收信号模型
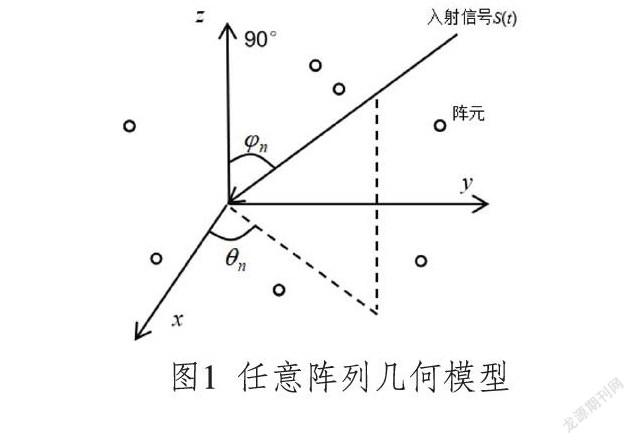
阵列由空间中不同位置的传感器构建,各个传感器即为阵列中的单个阵元。通常情况下阵元被看成是无尺寸的点,存在全向性等增益性。阵列信号处理即针对阵列接收信号实施处理。假设天线阵列的组成包含有M个阵元,且随意分布在三维空间中[4]。将编号为1的阵元作为参考阵元,将其位置作为坐标原点,以此构建空间坐标系,采用将编号为m(m=1,2,...,M)的阵元空间坐标表示出来。N个远场窄带信号在天线阵元中入射,采用将第n(n=1,2,...,N)个信号的入射方向表示出来。、分别为入射信号的俯仰角以及方位角,详情如图1所示。
2 基于DOA估計的阵列信号源仿真
高分辨算法可以实现信号角度的有效估计,然而对于先验条件的需求较多,如多重信号分类(Multiple Signal Classification,MUSIC)算法,需要了解信号个数,但是实际中难度较大。所以,在实际估计中通常不需要先验条件算法对其实施初步估计,而是在高分辨算法应用下实施角度估计,在多种算法应用下提升测角准确性。在本次分析中采用综合算法实施DOA估计,以提升估计准确度[5]。
在综合算法中,不需要先验已知信源数的算法针对目标实施估计,但就算是通过这些算法也无法对信号方位实施准确估计。然而,可以估计出信号中有所需要的信号。在本次分析中综合应用6种算法,估算中某个角度附近(1°范围内)出现5次及以上次数,即为期望信号方位。在此过程中,就能够实现对信号个数的估计,再次采用高分辨算法实施DOA估计,且在信源个数的应用下实施估计,采用高分辨算法实施验证,所得结果取平均值,即为想要获取的估计信号方位。
结合设置参数可以获取所需信号源数据,在以上DOA估计算法应用下对其实施仿真,获取某个角度附近(1°范围内)出现次数最多的角度,且在信源数估计方法以及MUSIC算法应用下对其实施估计,将获取角度计算平均值,即可以获取估计角度。
2.1 单频信号仿真
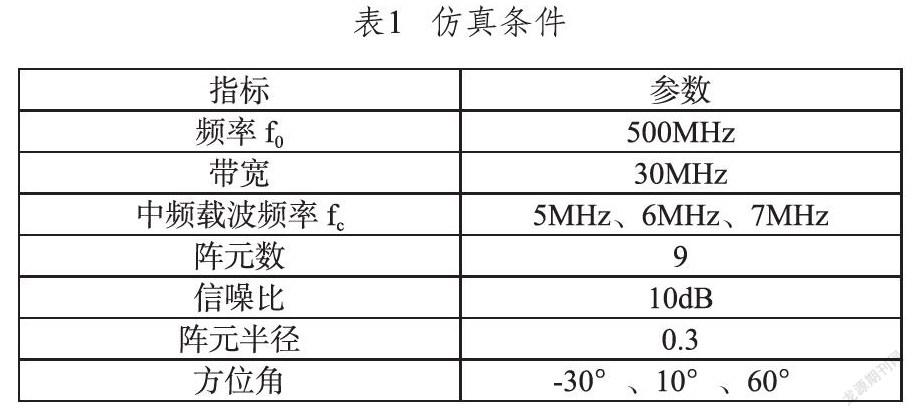
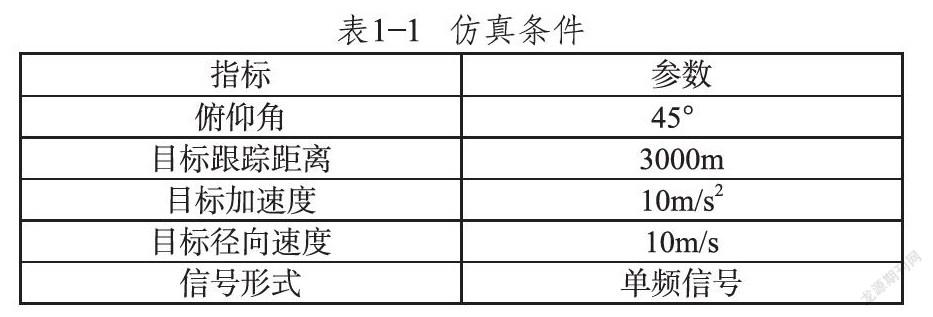
在对其实施仿真过程中,仿真条件具体如表1所示。
2.2 MUSIC算法估计
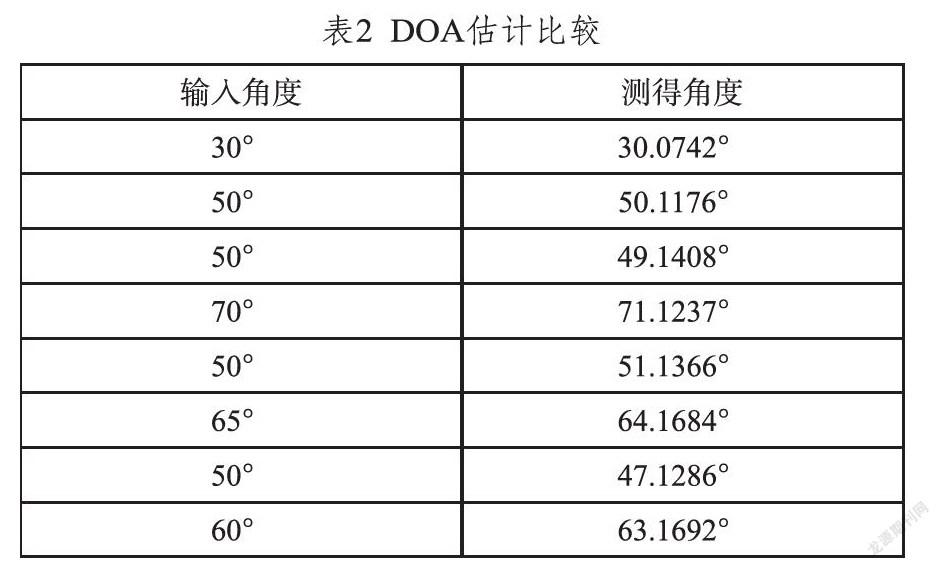
依照估计所得信号个数或采用信源个数估计算法估计的信源个数,在高分辨算法中输入以能够对其实施角度估计,在MUSIC算法应用下对其实施估计。结合阵列接收信号模型,以能够获取模拟信号源数据,在以上算法应用下实施估计,可以获取MATLAB仿真数据。从这一点可以看出,计算所得结果和信号角度接近度非常高[6]。其中,DOA估计对比结果如表2所示。
从表中可以看出,如果是在信号相互独立、同时位置差异较大的情况下,可以较为准确地估计各个信号方位;如果两个信号比较接近,对于信号方位角的估计难度则较大。依据测量数据可以发现,如果两个信号差异在15°之内,容易发生估计错误,部分情况下只能够估算出其中一个较为接近的信号。
2.3 通信信号仿真
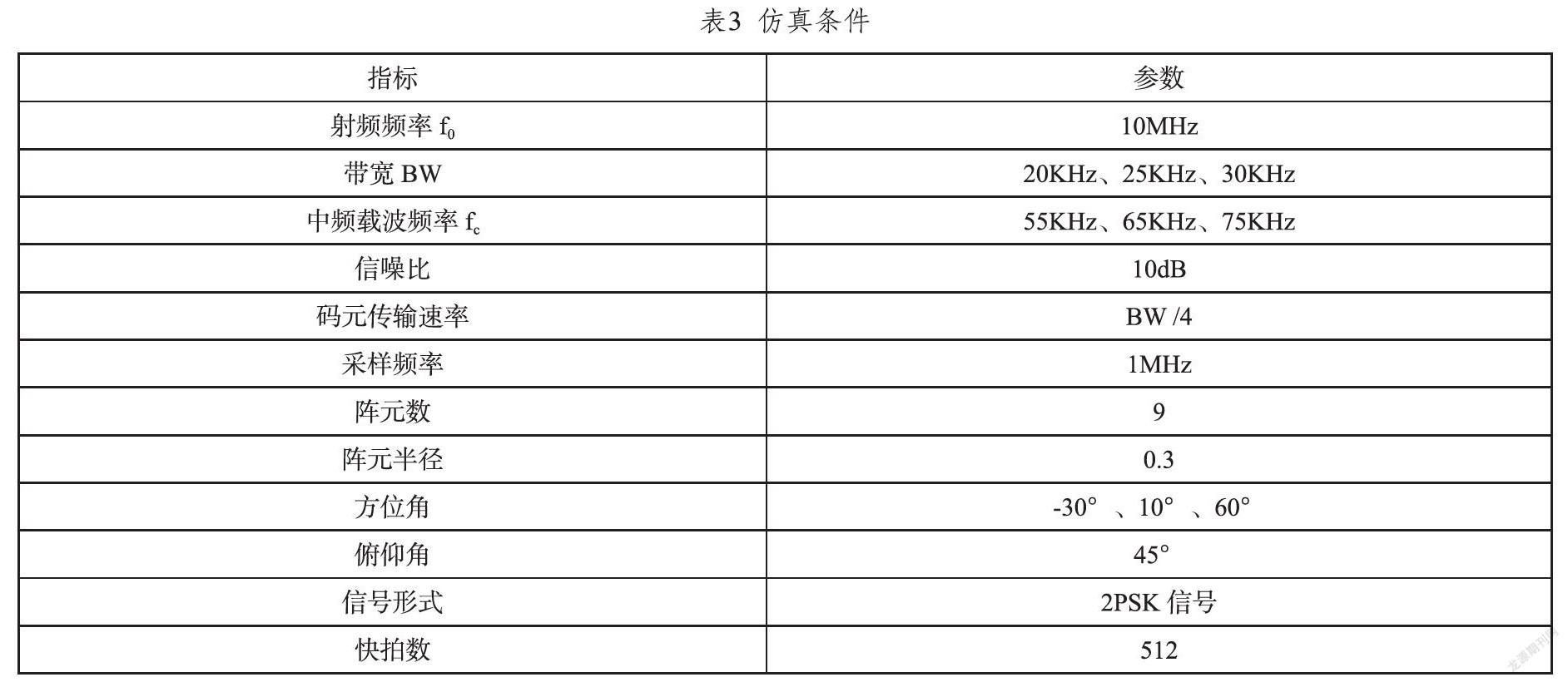
在对其实施仿真过程中,仿真条件具体如表3所示。
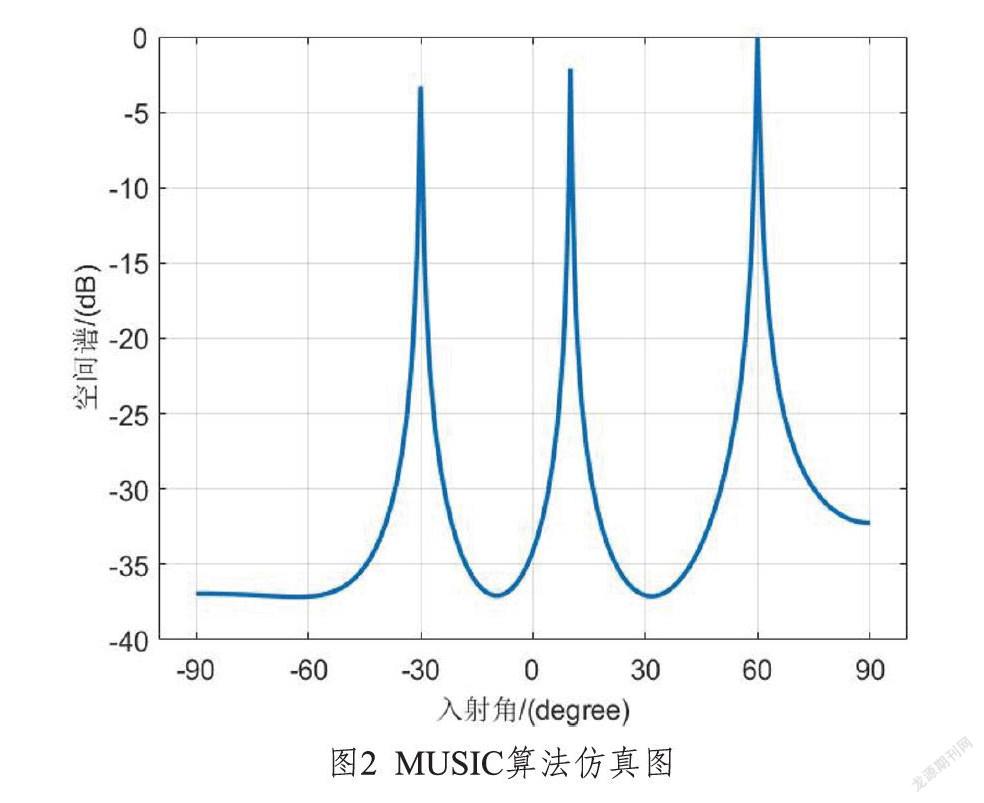
其中,在MUSIC算法应用下,所得仿真图如图2所示。
3 基于阵列误差的DOA估计
在实际工程中存在较多误差,通常阵列流型容易出现部分偏差和扰动。在此情况下,会直接影响到高分辨空间谱估计算法性能,严重时可能导致无法估计。之前,阵列校正实现方式为阵列流型直接测量、内插以及存储,然而实际应用中效果不佳也需要付出较大代价[7]。自20世纪90年代后,开始基于阵列扰动构建模型,以便将误差校正向参数估计进行转化。参数阵列误差校正通常包括两类方法,分别为有源校正类以及自校正类[8]。其中,有源校正类是在空间方位中已知辅助信源方位的前提下,离线估计阵列扰动参数。但是,自校正类方法则是结合某种优化函数,实现关于空间信源方位以及阵列扰动参数的联合估计[9]。
当前,阵列误差校正方法中主要包括有两种,分别为有源校正和自校正。有源校正,即在天线阵列接收校正源信号的应用下,估计分析阵列误差参数。其中,关于校正源个数以及方向等参数均为已知,之后在参数应用下校正接收信号,以此可以有效减少阵列误差对于不同阵列信号处理方法的影响。这一方法在应用中的优点是,可以在理想情况下实现对阵列误差影响作用的消除,计算量也不大。但是,需要针对校正源进行设置,增加了操作负担,在频繁校正中具有一定的不适用性。
自校正方法在阵列误差校正活动中,即便是没有校正源或缺乏先验知识的情况下也可以开展。当前,这一方法的基本思想是,针对空间谱和阵列误差实施联合估计。在测向过程中,也能够针对阵列误差参数实施估计,通常为构造代价函数。在关于其最优化问题的计算中,实现针对空间谱和阵列误差的联合估计[10]。这一方法在应用中无需校正源,操作较为简单,在频繁校正中较为适合。但是,通常会涉及到非线性多参量最优化问题,计算量比较大。
3.1 阵元幅相误差的校正方法
假设平面天线中存在着M个阵元,且没有方向性,存在着N个远场窄带信号,,...,在这一天线上入射,阵列输出信号矢量的表示方式为:
在以上公式中,,
,为空间来波信号;,代表的是第i个阵元中零均值同时方差为的高斯白噪声[11]。为第一个通道归一化第i个通道传输系数,表示为:,,。方向矩阵的表示方式为,是M行列向量,为第j个信号源的方向向量,为信号入射方向。
阵列输出协方差矩阵可以表示为:
在上式中,为的共轭转置矩阵,是信号向量的协方差矩阵,I是单位矩阵。针对特征值实施分解,也就可以获取相应噪声子空间,由此可发现在考虑天线幅相误差的情况下,对于MUSIC空间谱函数的修正结果可表示为:
所以,在校正过程中重点是求解误差矩阵。
3.1.1 校正原理
假设N个入射信号中已知方向校正信号个数为L个(L≥2且L≤N-1),相应代价函数即为:
在子空间基本原理应用下,可以获取误差矩阵向以下最小化问题进行转化,具体为:
因为在计算过程中,关于的计算公式为:
。
以上公式则可以转变为:
在以上公式中,假设,即存在有。假设目标函数为以下公式:
针对实现对r梯度的计算分析,且将其值等于零,即:。
将以上公式代入约束条件,即可以获取:
通过计算可获取r值,具体为:。
通过以上内容,即可以计算得出误差矩阵。但是,实际中所得结果为噪声子空间的估计值,因此需要对误差矩阵估计值进行计算。
3.1.2 仿真分析
假设阵列各通道增益和相位因子之间相关性,具体可以表示为:
在以上公式中出现的和为[0,1]内均匀分布的随机数,和为增益和相位因子方差,具体数值为:,,信噪比为10dB以及快拍数为1024。结合阵列幅相误差公式计算获取幅相误差,之后计算得到有幅相误差导向矢量以及有阵列幅相误差的阵列接收信号。
在仿真分析中假设天线阵为9元均匀圆阵,且均分分布,各阵元间距为0.5。远处存在有不相干信号,信噪比为20dB,角度为-60°、0°、30°。对其实施校正后所得曲线发现,这一情况下MUSIC谱线已失效,无法对信号实施估计,校正后三个信号方向上有尖峰存在,可以实现对信号方位角的准确估计。
3.2 阵元互耦校正方法
假设平面天线中存在有M个阵元,同时天线单元没有方向性,存在有N个远场窄带信号,,...,在这一天
线上入射,阵列输出信号矢量的表示方式为:
在公式(8)中,,
,为空间来波信号;,代表的是第i个阵元中零均值同时方差为的高斯白噪声。互耦矩阵C为M阶复方阵,方向矩阵的表示方式为:°
阵列输出协方差矩阵可以表示为:
针对特征值实施分解,也就可以获取相应噪声子空间,由此可发现在天线互耦误差存在情况下,修正MUSIC空间谱函数可表示为:
所以,在校正过程中重点是求解互耦矩阵C。
与阵元幅相误差校正方法一致,关于互耦矩阵C的求解,最终为求得互耦矩阵的估计值。通过仿真分析后,这一方法三个信号方向上存在尖峰,可以实现对信号方位角的准确估计。
3.3 阵元误差的自校正方法
假设平面天線中存在有M个阵元,同时天线单元没有方向性,存在有N个远场窄带信号,,...,在这一天线上入射,阵列输出信号矢量的表示方式为:
在公式(11)中,,
,为空间来波信号;,代表的是第i个阵元中零均值同时方差为的高斯白噪声。互耦矩阵C为M阶复方阵,方向矩阵的表示方式为。
阵列输出协方差矩阵可以表示为,通过以上计算可得阵列协方差为:
(12)
针对特征值实施分解,也就可以获取相应噪声子空间,由此可发现在天线互耦误差存在的情况下,修正MUSIC空间谱函数可表示为:
所以,在校正过程中重点是求解互耦矩阵C和幅相误差矩阵D。
与阵元幅相误差校正方法一致,最终为求得互耦矩阵的估计值以及误差矩阵估计值 。通过仿真分析后,这一方法三个信号方向上存在尖峰,可以实现对信号角度的准确估计。
4 结语
基于阵列信号的处理是波达方向估计的重要基础,文章首先分析了阵列接收信号的模型,然后综合使用DOA的估计算法进行了信号源的仿真,最后对阵列误差校正提出了不同的阵元误差处理方法。不同的处理方法有对应的修正MUSIC空间谱函数,在增加噪声无法估计信号源方向时,校正方法取得了良好的估计结果。
参考文献
[1] 汪子峰.阵列校正与信号源DOA估计和定位算法研究[D].成都:电子科技大学,2017.
[2] 戴峥.阵列误差校正与分布式信号源测向技术研究[D].南京:南京理工大学,2017.
[3] 张俊波.基于实测数据的阵列校正与测向研究[D].成都:电子科技大学,2015.
[4] 吴晗.存在互耦情况下的阵列测向技术研究[D].天津:天津大学,2015.
[5] 刘利国.基于虚拟天线及耦合自校正技术的抗干扰天线应用研究[D].哈尔滨:哈尔滨工程大学,2018.
[6] 谢坚.近场复杂源高分辨参数估计算法研究[D].西安:西安电子科技大学,2015.
[7] 李阳.DOA估计算法的改进及应用[D].南京:南京邮电大学,2015.
[8] 郑文艳.L型阵列的互耦误差秩损校正法的DOA估计方法[D].南京:南京邮电大学,2012.
[9] 任翠霞,王珍,段翔,等.考虑信源方位误差的阵元位置误差校正[J].雷达科学与技术,2015,13(04):390-394,409.
[10] 王敏,马晓川,鄢社锋,等.阵列幅度/相位误差的有源校正新方法[J].信号处理,2015,31(11):1389-1395.
[11] 张亚光.阵列接收信号模拟与DOA估计算法研究[D].成都:电子科技大学,2009.
