基于斋藤模型的滑坡临滑时间预报方法改进及应用*

亓 星 朱 星 许 强 赵宽耀 霍冬冬 王 浩 修德皓

（①四川轻化工大学土木工程学院，自贡643000，中国）

（②成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都610059，中国）

（③桥梁无损检测与工程计算四川省高校重点实验室，自贡643000，中国）

0 引 言

基于滑坡变形的科学监测预警模型和预报技术方法对有效防止滑坡灾害造成人员伤亡和减小经济损失具有重要意义，而滑坡临滑时间预报对于应急抢险和组织撤离具有重要的时间参考价值。目前，滑坡时间预报经历了长时间的发展，从最早的斋藤模型（Saito，1969），作图外延法模型（Hoek et al.，1977），到后续大量学者相继提出的灰色预报模型（陈明东等，1988）、Verhulst模型（晏同珍，1988）、黄金分割预报法模型（张倬元等，1998），尖点突变模型及灰色尖点突变模型（秦四清等，1993）、Verhulst反函数模型（李天斌等，1996）、速度倒数法模型（Segalini et al.，2018）等等，包括近年来基于已有数据的滑坡变形预测也得到了应用（秦四清等，2005；韩贺鸣等，2019；杨帆等，2019）。

通过梳理已有学者的研究发现，滑坡预报模型方法很多，算法各有差异，由此在滑坡临滑预报的应用中会出现预报时间的不同，但即使是相同模型，在不同计算区间下得到的时间预报值也会有明显差异，导致时间预报结果难以统一，对滑坡应急抢险、紧急撤离等需要较准确滑坡时间的处置工作增加了很大的困难。

事实上，滑坡预警和时间预报并非两个独立的过程，当滑坡进入加速变形并朝着失稳状态发展时，预警模型可及时判断滑坡的危险性（Fan et al.，2019），同时预报模型需要准确计算滑坡失稳时间，为针对性的应急处置提供可靠的时间数据，而目前并没有学者结合滑坡预警进行可靠的临滑时间预报研究。由此，本文针对现有滑坡时间预报中计算区间不统一的问题，通过预警切线角模型将不同滑坡变形数据无量纲化，并基于斋藤预报模型提出改进的临滑时间预报方法，为滑坡应急处置提供统一可靠的时间参考。

1 滑坡临滑时间预报方法的改进

滑坡应急抢险等实际应用中需要快速对滑坡发生时间进行初判，并结合预警等级确定抢险时间和撤离方案。在满足一定准确度的条件下，需要临滑时间预报模型简单易用，而斋藤时间预报模型正好符合这一要求，其早在1970年就成功预报了日本高汤山滑坡，具有一定的可行性，且不需第三方软件即可计算预报结果，具体方法为：选取变形曲线中t1、t2、t33个时间节点，确保其时间间隔内的变形量相等，则从t3开始，滑坡发生剩余时间T＝0.5（t2－

近年来，通过智能变形监测设备，获取了多个典型滑坡的全过程变形数据，如2019年2月17日发生在贵州兴义的龙井村滑坡，2017～2019年发生在黑方台的多次黄土滑坡，为滑坡时间预报方法的研究提供了良好的数据支持。

1.1 时间预报计算区间的确定

临滑时间预报是针对滑坡进入加速变形后，对短期内即将发生的滑坡进行时间预报。在实际应用中发现，即使是相同的时间预报方法，由于变形数据计算区间的不同也会导致结果的差异，因此，为避免计算区间差异导致预报时间不一致，影响时间预报的可靠性和稳定性，可尝试建立对各类变形曲线都有普适性的统一变形计算区间。

由于不同类型的滑坡对应的变形曲线也各不相同，无法直接通过时间节点或变形速率确定相同计算区间，但滑坡变形曲线可以通过坐标变换进行无量纲处理，转换为切线角变化曲线（许强等，2009），使各种滑坡变形曲线可以在相同切线角特征下比较。切线角模型将滑坡变形曲线划分为初始变形、匀速变形和加速变形3个阶段，并通过切线角大小反映滑坡危险程度，计算公式为 α＝arctan（V／V1）。式中，V为滑坡实际变形速率，V1为滑坡匀速变形阶段变形速率。当切线角大于45°时，认为滑坡进入了加速变形阶段，这一阶段又可细分为初加速（45°～80°）、中加速（80°～85°）、加加速（＞85°）变形阶段，切线角越接近90°，滑坡越接近发生。

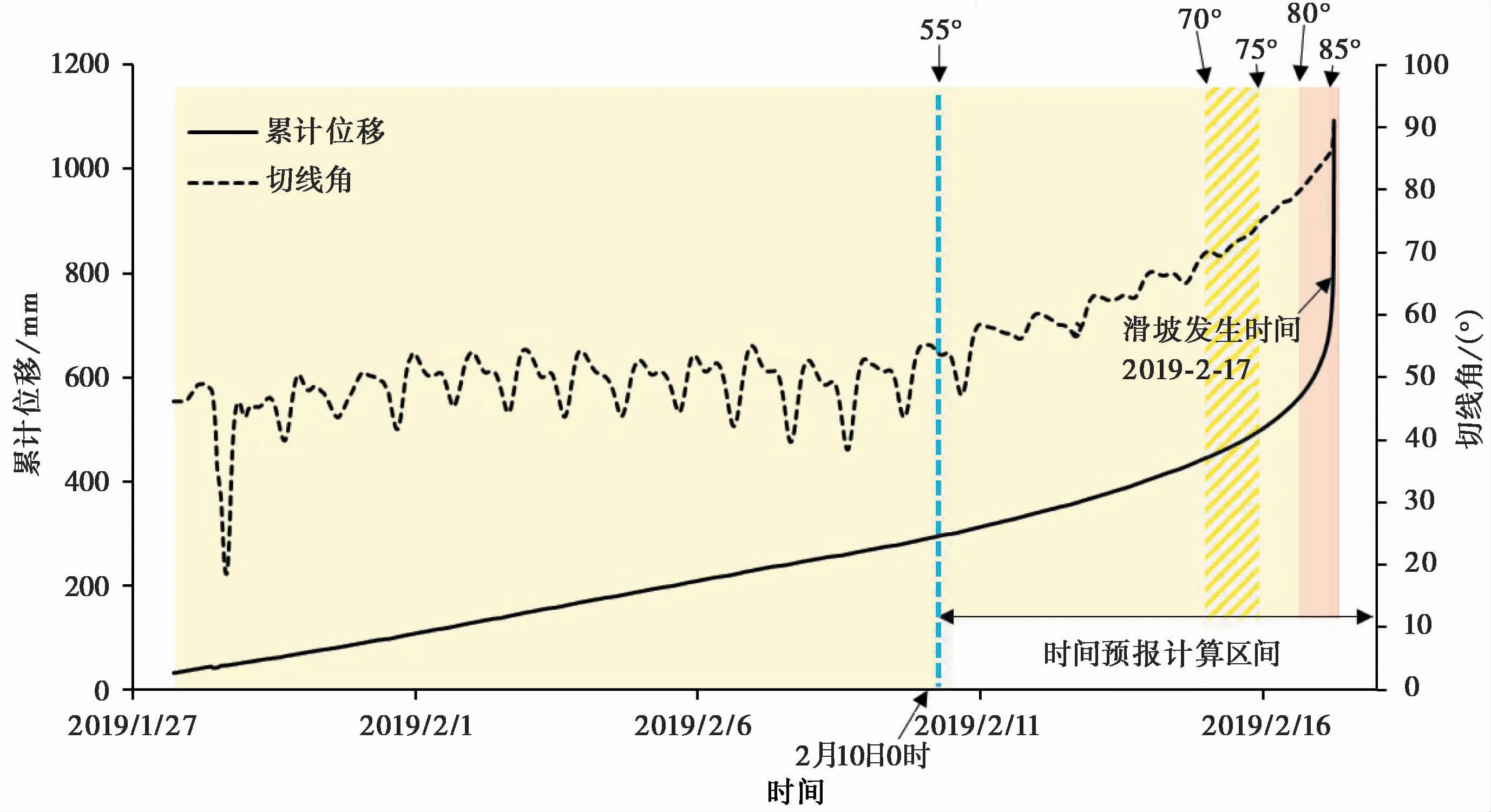
图1 龙井村滑坡1＃点变形数据Fig.1 Deformation data of 1＃point of Longjingcun landslide

以2017年2月17日龙井村滑坡1＃位移计获取的精细化变形数据为例，首先计算出对应的滑坡切线角变化特征（图1），再选取滑坡前7 d的2019年2月10日0时作为起算点，随时间逐渐接近滑坡发生的过程中，不断利用斋藤时间预报模型计算滑坡发生剩余时间，并获取计算剩余时间与实际剩余时间的偏差值（图2纵坐标），获取偏差值与滑坡失稳剩余天数的关系。以此类推，得到不同时间起算点对应的预报偏差值与滑坡剩余天数的关系（表1，图2），分析数据后发现，时间预报的起算点越早，最终计算的临滑时间预报偏差值反而越大。分析预报偏差与切线角的规律发现，滑坡预报时间偏差值随着滑坡的临近而趋于稳定，其在变形切线角超过75°以后不再有明显波动，即使计算点达到临滑点，偏差值也不会减小。

图2的趋势说明，时间预报计算区间的起点太早会增大预报偏差值，滑坡进入加速变形时，切线角＞45°，随着变形逐渐加快，切线角也相应增大，在初加速变形阶段（45°～80°）的前期，加速变形趋势不明显，且距离滑坡实际发生时间还较长，任何轻微的波动都会导致时间预报产生较大的差异；而计算区间结束点过晚也并不能减小偏差，同时，计算点越晚，滑坡越接近失稳，当切线角超过80°后，滑坡进入中加速阶段，随着切线角继续增大，甚至进入加加速变形阶段，时间预报提前量越来越小，对于滑坡应急处置等工作也越不利。根据龙井村滑坡变形数据发现，当切线超过75°后时间预报值基本稳定。

为证实时间预报中滑坡变形对应切线角在70°～75°时，计算的偏差相对稳定且具有普适性，以2017年5月13日发生在甘肃省盐锅峡镇的黑方台陈家6＃黄土滑坡精细变形数据为例进行验证。陈家6＃滑坡变形虽然表现出一定的突发性，但通过计算切线角，并采用斋藤预报模型仍然能反映出较明显的规律，即不同起算点进行时间预报计算的偏差在切线角超过75°以后逐渐稳定（图3）。

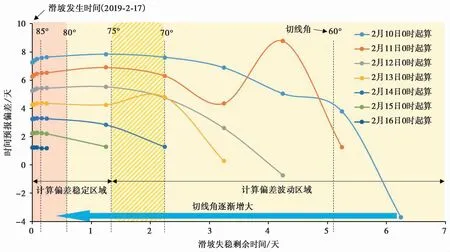
图2 龙井村滑坡1＃点不同起算点斋藤预报模型偏差特征Fig.2 Deviation characteristics of saito prediction model at different starting points of Longjingcun landslide

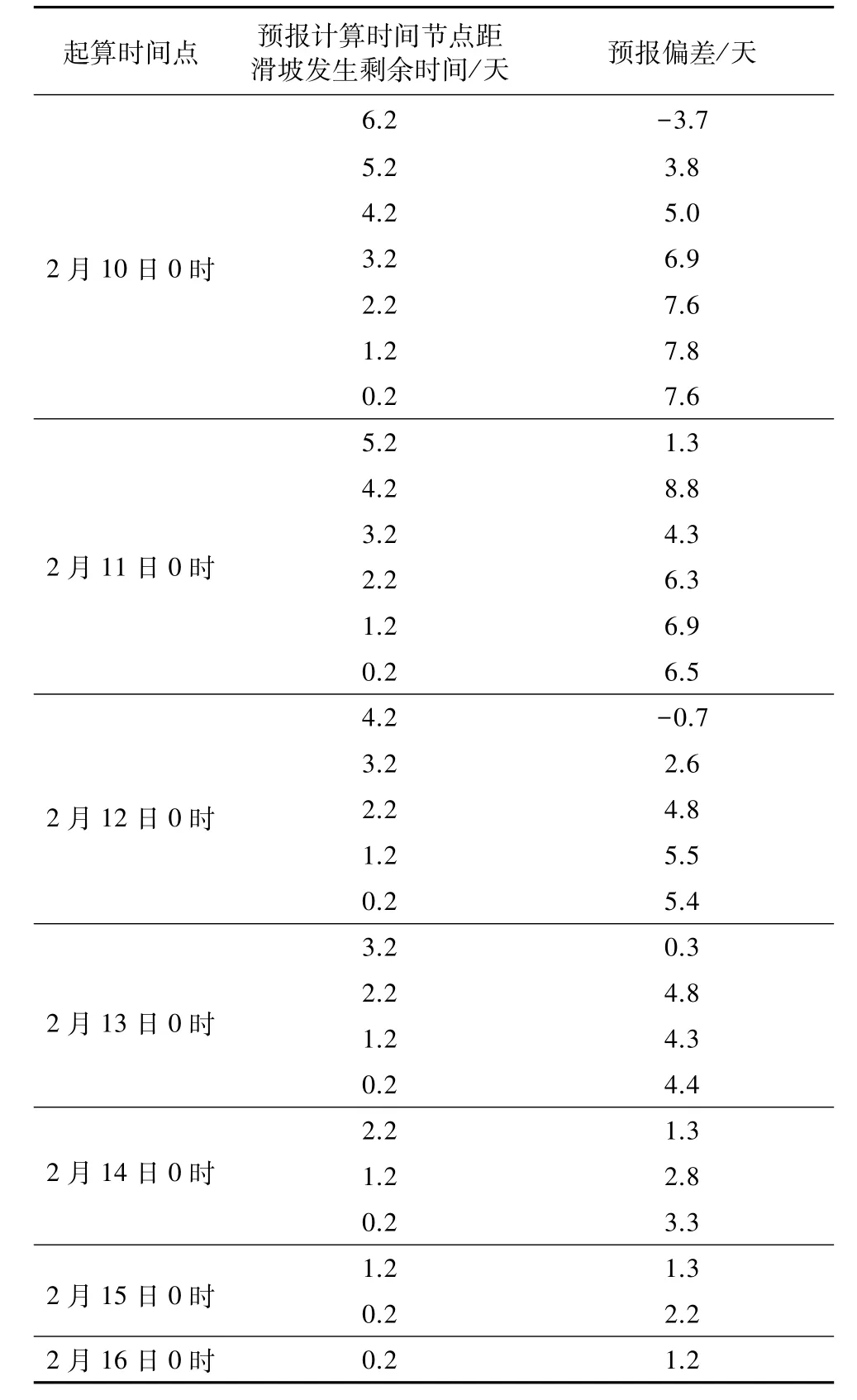
表1 龙井村滑坡不同预报时间点对应的预报误差Table 1 Forecast errors of Longjingcun landslide at different forecast time points

综合考虑滑坡预报偏差的稳定性和起算点的影响，可以以切线角70°～75°作为滑坡临滑时间预报的计算区间，以此实现不同滑坡变形曲线计算区间的统一，避免计算区间差异导致滑坡时间预报的差异（图4）。

1.2 时间预报计算值的修正

在滑坡临滑预报的实际应用中发现，现有滑坡临滑时间预报方法还存在预报时间偏晚的问题，龙井村滑坡前3天利用斋藤模型计算得到的滑坡时间比实际滑坡时间滞后超过3 d，而其他临滑时间预报模型计算结果仍然偏晚。分析近年来通过智能位移计获取的多个滑坡精细变形曲线（亓星，2017）后发现，滑坡进入加加速变形阶段后，变形速率会在已有加速增长的基础上再次陡增，表现出累计位移曲线出现明显的上翘特征，与一般临滑预报模型所拟合的光滑曲线不完全相符，使预报时间比实际发生时间偏晚，可能对滑坡应急处置等防灾工作带来潜在威胁。

变形曲线出现明显的陡增，其内在变化体现在变形切线角的迅速增大，滑坡提前发生对应了切线角的非线性增长。通过模拟滑坡变形时切线角的变化特征发现：当切线角匀速增大时，切线角斜率为常数，此时选取切线角在70°～75°区间的变形数据进行斋藤时间预报，计算的滑坡失稳时间与实际失稳时间完全一致；而当预报区间的变形切线角加速增大时，其切线角斜率也相应增大，滑坡变形会在逐渐增长的基础上再次加速，使滑坡发生时间提前（图5a），表现为切线角的斜率由a1增大至a2时，滑坡发生时间由t2提前至t1，两者包含的面积相等，即a2／a1＝t2／t1（图5b）。

以贵州龙井村滑坡1＃智能位移计变形和切线角数据为例（图6），采用70°～75°切线角作为时间预报计算区间，其切线角平均斜率为5.8，由此计算滑坡在2.4 d后发生。而切线角75°至滑坡发生期间的实际平均斜率增大至11.5，增加了约一倍，对应实际滑坡时间为1.3 d后发生，滑坡发生时间也大致缩短为原预报时间的1／2。由此发现，滑坡提前发生表现出加速变形阶段中切线角的斜率增加的现象，而通过计算切线角斜率增加值在时间上的积分量，可以计算出滑坡实际发生时间相对于预报时间的提前量。

分析现有精细化监测获取的大量变形曲线特征发现，当切线角从75°增大至接近90°期间，变形曲线都存在明显的陡增，表现为切线角的斜率进一步增大，而不同滑坡变形曲线中加速变形阶段相似的特点，使时间提前量可通过大致相同的修正系数确定，在应急抢险等需要快速估计滑坡失稳时间时，其折减值不用精细积分计算切线角斜率增加量与滑坡时间减少量的关系来确定。由此，以贵州龙井村滑坡变形数据为例，根据其切线角斜率增加了一倍的规律，定义修正系数值0.5作为改进斋藤模型的时间预报修正系数，即以滑坡变形切线角70°～75°为计算区间计算出滑坡失稳剩余时间，再乘以折减系数0.5得到最终滑坡失稳时间。

图3 陈家6＃滑坡不同起算点斋藤预报模型偏差特征Fig.3 Deviation characteristics of saito prediction model at different starting points of Chenjia 6＃landslide

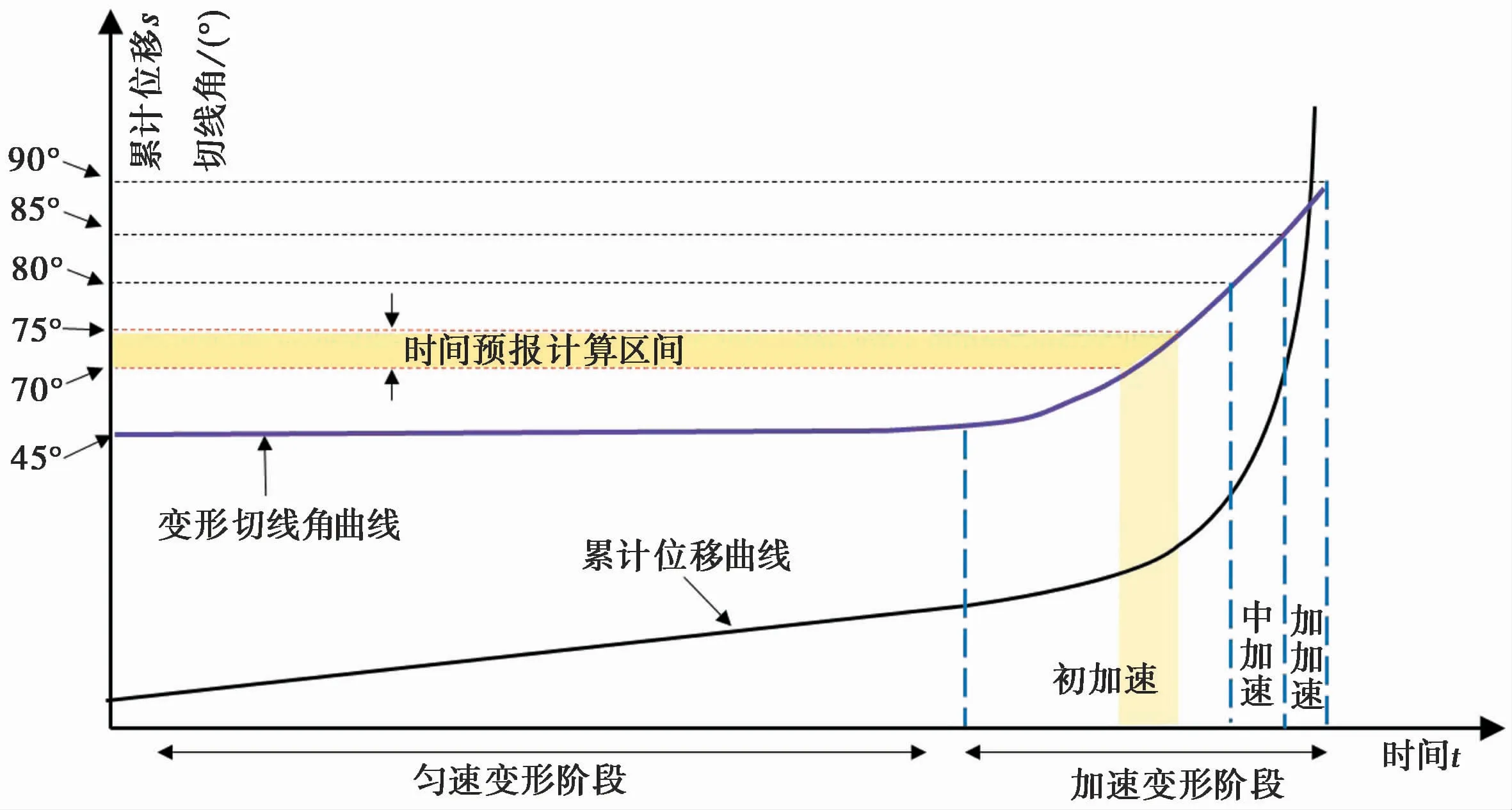
图4 滑坡时间预报计算区间示意图Fig.4 Interval diagram of time prediction of landslide

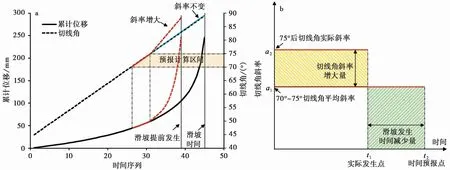
图5 切线角斜率变化与滑坡发生时间的关系Fig.5 Relation between tangential gradient change and landslide occurrence time

2 临滑时间预报方法应用实例

2.1 贵州兴义龙井村9组滑坡

2019年2月17日凌晨5点53分，贵州省黔西南州兴义市龙井村9组发生了一起深层顺层岩质滑坡，超过60万立方米山体失稳破坏，直接威胁了滑坡下游数百人的安危，由于本团队成员提前近1 h发布了红色预警，结合现场科学管理和处置，该滑坡并未造成人员伤亡和财产损失。

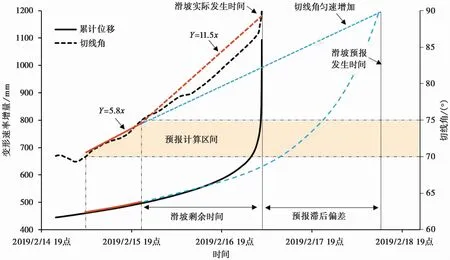
图6 贵州龙井村滑坡斋藤预报时间和滑坡发生时间关系Fig.6 The relationship between the time of landslide prediction and the time of landslide occurrence in Longjingcun，Guizhou

龙井村滑坡为深层顺层岩质滑坡（图7），2014年该处曾发生一次小规模滑动，在东侧形成了高约25 m的垂直临空面，后缘也形成了新的裂缝并不断发展，对滑坡下方400余人的生命安全造成了严重威胁。2019年1月起，随着智能化监测设备的布设，滑坡变形过程得到精确掌控（图7），至2月12日开始，滑坡出现明显的变形加快趋势。以布设的1＃裂缝计为例（其余正常工作的裂缝计进入加速变形阶段的时间基本一致（亓星，2019）），2019年2月14日23点，裂缝计变形对应的切线角达到70°，累计位移444.4 mm，2月15日22点，切线角达到75°，累计位移496.9 mm。根据改进的斋藤时间预报模型，在变形对应的切线角达到75°时进行时间预报，预报计算区间为切线角70°～75°对应的变形量，并将计算值折减0.5倍，得到滑坡预报时间为2019年2月17日2点10分，提前32 h做出时间预报，与实际滑坡发生时间相差不足4 h，而未折减的原始斋藤时间预报模型计算滑坡发生时间为2月18日6点20分，误差超过24 h。

2.2 甘肃黑方台黄土滑坡

图7 龙井村滑坡前后对比Fig.7 Comparison of landslide in Longjingcun

黑方台位于我国西北黄土地区，地处甘肃省永靖县盐锅峡镇，是灌溉诱发的黄土滑坡集中发育区，由于常年灌溉每年在台塬边会产生多次黄土滑坡。近年来，结合早期识别工作在可能发生滑坡的区域布设了多个位移监测设备，成功获取了黑方台多次黄土滑坡的完整变形数据（图8）。

陈家6＃滑坡位于黑台东北侧磨石沟右岸，滑源区长116 m，宽165 m，为典型的突发型黄土滑坡。2017年5月13日，陈家6＃滑坡产生了一次滑动，滑坡体积不足1×104m3。党川4＃滑坡和党川6＃滑坡位于甘肃省永靖县盐锅峡镇黑方台西南侧黄河边，党川4＃滑坡自2017年8月底开始产生变形并逐渐加速，2017年10月1日凌晨5时许，党川4＃滑坡附近连续产生滑动，在滑源区形成了3个凹槽，并在滑坡下方形成了超过300 m长的堆积体。党川6＃滑坡也为突发型黄土滑坡，自2019年3月24日后变形开始加快，并于2019年3月26日凌晨产生滑动。由于针对几次滑坡都布设了有效的监测设备，并通过完整的滑坡变形数据成功提前预警，并未造成人员伤亡。

分析黑方台数次黄土滑坡的变形数据，以变形对应的切线角在70°～75°作为计算区间，根据改进的斋藤时间预报模型进行计算并折减0.5倍，得到滑坡预报时间和实际发生时间（表2）。

由表2可见，即使是具有一定突发性的黄土滑坡，改进的斋藤时间预报方法计算的滑坡失稳时间精度均优于改进前，预报偏差值更小，且计算区间的明确使得不同的人采用相同方法计算出的时间预报值基本一致。

由此，本文提出的基于斋藤时间预报模型的滑坡变形临滑时间预报方法具有较强的普适性，可以用于多种类型的滑坡临滑时间预报。在需要精确判断滑坡发生时间时，还可根据变形数据实际切线角的斜率变化量，精确确定出滑坡发生时间的提前量。

3 结论与认识

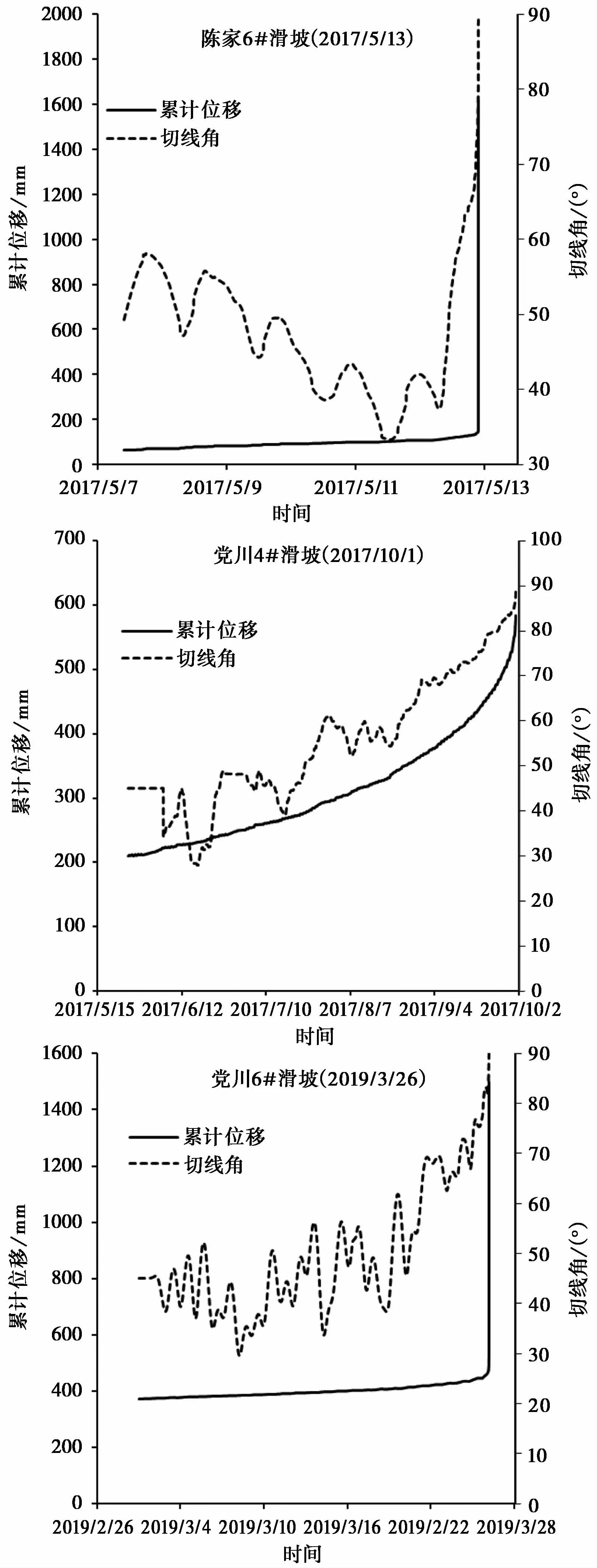
图8 黑方台多次黄土滑坡变形曲线Fig.8 Deformation curve of Heifangtai loess landslide

表2 改进后的黑方台黄土滑坡临滑时间预报比较Table 2 Short-term time prediction comparison by Heifangtai loess landslide

（1）针对现有滑坡临滑时间预报模型计算区间不统一导致相同预报方法结果不同的问题，以斋藤时间预报模型为例，通过分析时间预报偏差与选取计算区间的差异规律，提出了以变形切线角70°～75°作为计算区间，避免了过早计算导致时间预报偏差过大和过晚计算应急处置时间不足的问题。

（2）实际应用中考虑加速变形阶段切线角斜率不断增大导致滑坡发生时间提前的特点，通过实际斜率与计算区间斜率的比值修正滑坡预报时间，并基于统计初步确定修正值为0.5，由此在滑坡应急处置期间可直接采用修正系数对各类变形计算预报时间进行修正。以贵州龙井村滑坡和甘肃黑方台多个滑坡的精细变形数据检验表明，改进后的滑坡临滑时间预报可应用于多种滑坡，预报时间更为精确，且具有一定的普适性。

（3）滑坡时间预报是滑坡灾害防治的重要内容之一，随着监测技术的不断发展，今后基于多源数据协同的科学时间预报模型也将进一步提升滑坡预报的可靠性，在地质灾害防治中发挥重要作用。