蚕蛹热泵干燥特性及其动力学模型研究
2020-09-10吴钊龙林芳陈振林莫嘉华杨艳兰
吴钊龙,林芳,陈振林,*,莫嘉华,杨艳兰
(1.大连工业大学食品学院,辽宁大连116034;2.贺州学院食品科学与工程技术研究院,广西贺州542899)
蚕蛹又名小蜂儿,蚕蛾科,是蚕发育到一定阶段的产物,桑蚕业的附属品,而且是卫生部批准的作为普通食品管理的食品新资源中唯一的昆虫类食品[1-2]。我国蚕蛹资源非常丰富,年产蚕蛹30万t以上,约占全世界总产量的80%[3-4]。蚕蛹不仅具有很高的营养价值,还具有多种药理作用,其营养价值可与牛奶、鸡蛋相媲美[5]。蚕蛹蛋白质中含有18种氨基酸,其中8种人体必需氨基酸占总氨基酸的42%,必需氨基酸与非必需氨基酸的比例达到0.7∶1.0,非常符合联合国粮农组织及世界卫生组织建议的理想氨基酸模式[6-7]。蚕蛹因为富含人体所必需营养和活性成分而在食品、医药、化工等行业有着广泛的用途,非常符合当今人们对高蛋白低脂肪的膳食消费需求[8-9]。
目前,有关蚕蛹综合利用的研究已经逐渐开展起来,干燥是一种通过将物料中的水分降低到一定程度而获得干制品的方法,对食品贮藏期太短而造成浪费的问题可以有效地解决[10]。热泵干燥是一种具有节能、高效和提高干燥产品品质的新型干燥方法[11-12]。目前对于昆虫的干燥加工研究尚处于初级探索阶段,尤其是采用热泵干燥方法加工昆虫的有关研究更是鲜有报道,迄今还未见有采用热泵干燥方法干燥蚕蛹的研究报道。本研究以蚕蛹为原料,探究不同干燥温度、不同铺料密度两个条件对蚕蛹热泵干燥特性的影响,构建关于蚕蛹热泵干燥的动力学模型,并对试验结果进行验证,为蚕蛹干制深加工提供理论依据。
1 材料与方法
1.1 材料
蚕蛹:广西平乐国弘茧丝绸有限公司。
1.2 试验设备
WRH-100AB型环闭除湿热泵干燥机:正旭新能源设备科技有限公司;JJ1000型电子天平:常熟市双杰测试仪器厂;MB90型水分测定仪:奥豪斯仪器常州有限公司。
1.3 试验方法
1.3.1 工艺流程
冷冻蚕蛹→清洗→漂烫→沥干→摆盘→热泵干燥→成品
1.3.2 干燥温度对蚕蛹热泵干燥特性的影响
在恒定风速,湿度为25%,铺料密度为0.6 g/cm2条件下,分别考察干燥温度为45、55、65、75℃时对蚕蛹热泵干燥特性的影响。在干燥过程中,相隔15min取一次样,使用MB90型快速水分测定仪测定样品湿基水分含量,直至干燥至湿基含水量小于5%为止。
1.3.3 铺料密度对蚕蛹热泵干燥特性的影响
在恒定风速,温度为65℃,湿度为25%的条件下,分别考察铺料密度0.4、0.6、0.8 g/cm2对蚕蛹热泵干燥特性的影响。在干燥过程中,相隔15 min取一次样,使用MB90型快速水分测定仪测定样品湿基水分含量,直至干燥至湿基含水量小于5%为止。
1.4 测定方法
1.4.1 含水量的测定方法
通过用MB90型快速水分测定仪测定蚕蛹的含水量。得到蚕蛹平均初始含水量为76.39%。蚕蛹干基含水量根据式(1)计算:

式中:M为蚕蛹热泵干燥到t时刻时的干基含水量,g/g;W为蚕蛹热泵干燥到t时刻时的湿基含水量,g/g。
1.4.2 干燥速率的测定方法

式中:DR为干燥速率,g/(g·min);Δt为相邻2次测定蚕蛹的时间间隔,min;Mt+Δt为干燥至 t+ Δt时刻蚕蛹的干基含水量,g/g;Mt为干燥至t时刻蚕蛹的干基含水量,g/g[13]。
1.4.3 水分比的测定

式中:MR为水分比;Mt为干燥至t时刻蚕蛹的干基含水量,g/g;Me为蚕蛹平衡干基含水量;M0为蚕蛹初始干基含水量;由于蚕蛹的平衡干基含水量Me远远小于Mo和Mt,通常可以忽略不计,因此,可将式(3)简化成式(4)进行计算[14-15]:

1.4.4 干燥模型的拟合
本试验选用了5种最常见的干燥模型对蚕蛹的干燥模型进行线性拟合[16],有利于对试验数据进行分析处理,5种动力学模型及其表达式见表1。
1.4.5 数据分析
试验数据分析处理用SPSS 19.0软件。
2 结果与分析
2.1 蚕蛹热泵干燥特性
2.1.1 干燥温度对蚕蛹热泵干燥特性的影响结果
在恒定风速,湿度为25%,铺料密度为0.6 g/cm2条件下,不同温度的蚕蛹热泵干燥曲线如图1所示。
由图1知,蚕蛹热泵干燥曲线相对比较光滑,蚕蛹干基含水量随着干燥时间的延长呈现出逐渐下降趋势,蚕蛹干燥到一定程度后干燥曲线逐渐趋于平缓;蚕蛹干燥特性易受温度的影响,随着温度升高蚕蛹热泵干燥曲线越陡峭,达到相同含水量时的时间也就越短;当温度为75℃时,达到平缓的时间为180 min,而温度为45℃时,达到平缓的时间为415 min,这与叶维等[17]研究魔芋热泵干燥特性时发现干燥温度对魔芋干燥曲线影响较大的研究结果一致。因为随着干燥温度的上升会使蚕蛹表面水分迅速蒸发,还可以将空气的相对湿度降低,蚕蛹表面的湿度与空气介质的湿度相差越大,蚕蛹水分的挥发就会越快,使蚕蛹表层水分向干燥气体的扩散动力增加,进而缩短蚕蛹的干燥时间[18]。表明蚕蛹在相同初始干基含水量,干燥温度不同的情况下,物料水分变化存在显著差异。干燥速率曲线如图2所示。

表1 5种动力学模型及其表达式Table 1 Five kinetic models and their expressions

图2 不同温度蚕蛹热泵干燥速率曲线Fig.2 Heat pump drying rate curves of silkworm pupa at different temperatures
由图2可知,干燥温度为75℃的失水速率明显高于干燥温度为45℃的失水速率。在不同温度下温度越高,蚕蛹干燥速率曲线变化就越陡峭,所需的干燥时间就越短,恒速阶段越不明显。蚕蛹干燥速率随着干基含水量的变化而变化,随着干基含水量的降低,4条曲线均存在明显的增速阶段和降速阶段。蚕蛹在干燥温度为45℃和55℃时出现明显的恒速期约为80 min~120 min,而在干燥温度为65℃时出现短暂的恒速期约为50 min~70 min,在干燥温度为75℃时未出现明显的恒速期,随后均逐渐下降,降速阶段占绝大部分。出现明显的恒速期是因为蚕蛹表面水分蒸发与内部水分迁移之间保持短暂的恒定,在整个干燥过程中,降速期占大部分是因为干燥初期蚕蛹表面水分会在空气中扩散较快而且失水速率相对较高,因此不易形成恒定的水分浓度差,从而加速阶段和恒速阶段相对于降速阶段来说持续时间较短,而随着蚕蛹表层水分降至一定程度后,水分从内部向表层迁移的速率减慢,失水速率下降变慢[19-20]。
2.1.2 铺料密度对蚕蛹热泵干燥特性的影响结果
在恒定风速,温度为65℃,湿度为25%的条件下,不同铺料密度对蚕蛹热泵干燥的影响如图3、图4所示。
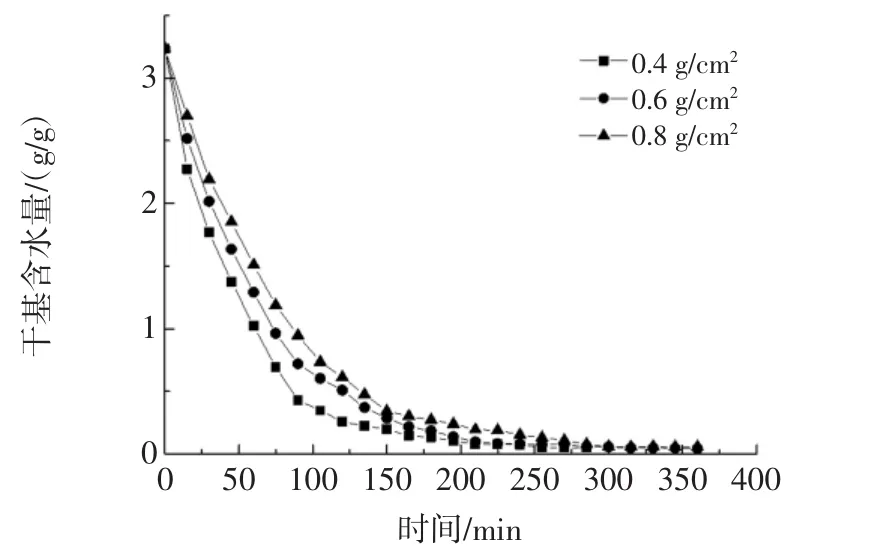
图3 不同铺料密度蚕蛹热泵干燥曲线Fig.3 Heat pump drying curves of silkworm pupa at different traying density

图4 不同铺料密度蚕蛹热泵干燥速率曲线Fig.4 Heat pump drying rate curves of silkworm pupa at different traying density
由图3可知,铺料密度是影响蚕蛹热泵干燥的重要因素,不同铺料密度蚕蛹干燥曲线线形相似,随着干燥时间的延长,蚕蛹干基含水量逐渐减小。铺料密度为0.4、0.6、0.8 g/cm2的蚕蛹在65℃下干燥时,干基含水量降低至趋于平缓的含水量分别需要190、230、300 min。蚕蛹铺料密度越大,含水量降低越慢,干燥曲线趋于平缓时间就越长。由于铺料密度不同蚕蛹形成的水分梯度大小也不同,会有不同的水分驱动力形成,所以在不同的铺料密度、相同的干燥时间情况下蚕蛹的含水量有所不同[21]。
由图4可知,铺料密度对蚕蛹干燥速率影响较大,3条不同铺料密度的干燥速率曲线均有明显加速阶段,随后迅速下降,在整个干燥过程中降速阶段占大部分。铺料密度为0.8 g/cm2时存在明显恒速期约为80 min~100 min,铺料密度为0.4 g/cm2和0.6 g/cm2时未出现明显的恒速期,即随着铺料密度的减小,恒速期越不明显。3条曲线均表现出明显降速阶段转折点,但是不同铺料密度的干燥速率曲线转折点处蚕蛹水分含量有明显差异。这是因为在温度相同的情况下,在蚕蛹热泵干燥初期阶段产生的热量主要用来提高蚕蛹自身的温度,随着铺料密度的增加,因此水分蒸发所需热量也就越多,从而干燥速率会越缓慢。
2.2 蚕蛹热泵干燥模型的建立
2.2.1 蚕蛹热泵干燥过程试验数据的拟合
按照1.4.4选用的5种最常见干燥动力学模型,对蚕蛹热泵干燥过程进行线性拟合,干燥动力学模型中Newton、Henderson and Pabis、Lagarithmic的-lnMR-t均为线性关系,干燥模型Wang and Singh的MR-t为线性关系,Page模型的ln(-lnMR)-ln t为线性关系。因此分别以不同干燥温度和铺料密度下,蚕蛹热泵干燥过程 MR、-lnMR、ln(-lnMR)为纵坐标,t、t、lnt分别为对应的横坐标作图。结果如图5~图7所示。
由图5可知,不同干燥温度和铺料密度下,蚕蛹热泵干燥过程MR-t是非线性关系,因此,Wang and Singh模型不适合用来描述蚕蛹热泵干燥。
由图6可知,不同干燥温度和铺料密度下,蚕蛹热泵干燥过程-lnMR-t是非线性关系,因此,Lagarithmic、Henderson and Pabis、Newton 3 种模型不适合用来描述蚕蛹热泵干燥。
由图7可知,不同干燥温度和铺料密度下,蚕蛹热泵干燥过程ln(-lnMR)-lnt是线性关系,所以Page模型可以描述和预测蚕蛹热泵干燥。
经计算得到Page模型拟合方程中的系数R2=0.990,表明Page模型适合用于不同干燥温度和不同铺料密度条件,所以Page模型可以适用于蚕蛹热泵干燥动力学模型。
2.2.2 蚕蛹热泵干燥动力学模型的建立
采用Page模型ln(-lnMR)=lnk+nlnt建立蚕蛹热泵干燥动力学模型,令:

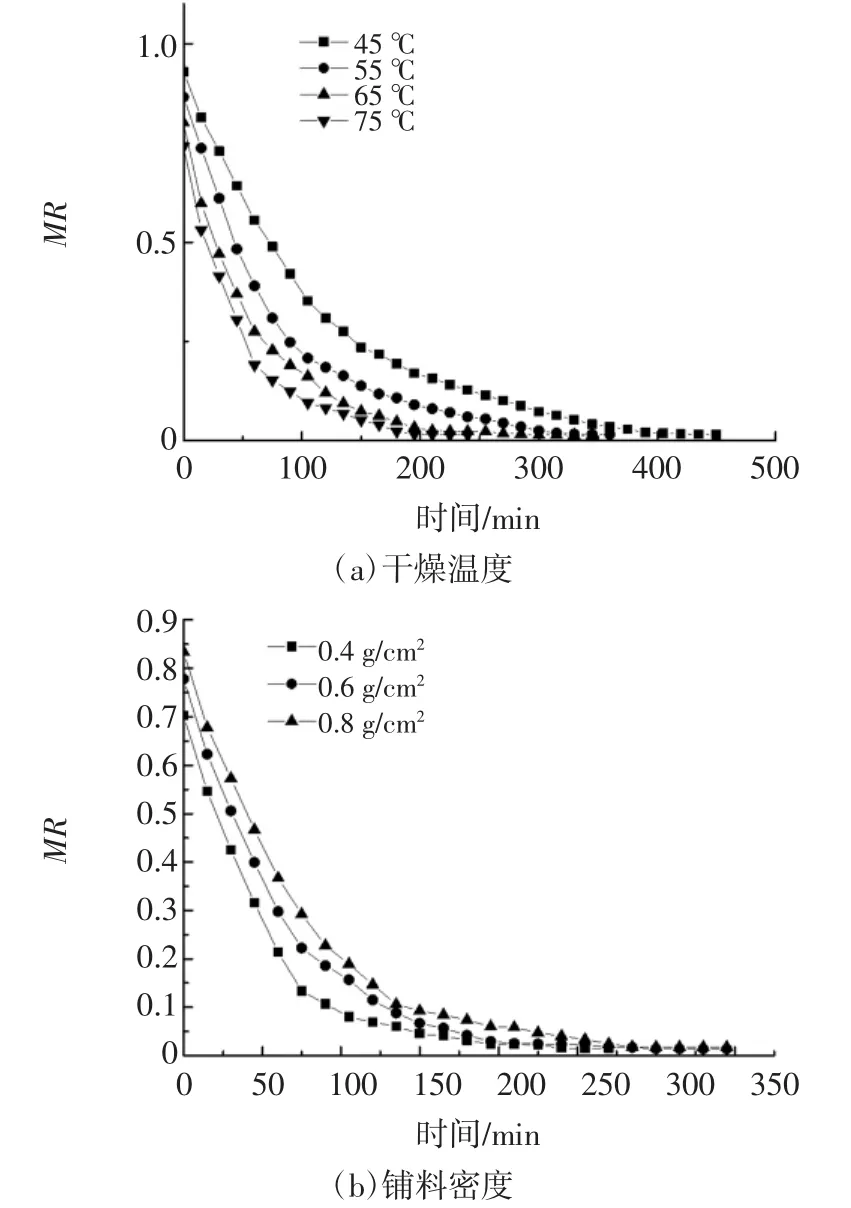
图5 不同条件蚕蛹热泵干燥过程MR-t曲线Fig.5 MR and t of silkworm pupa heat pump drying process under different conditions
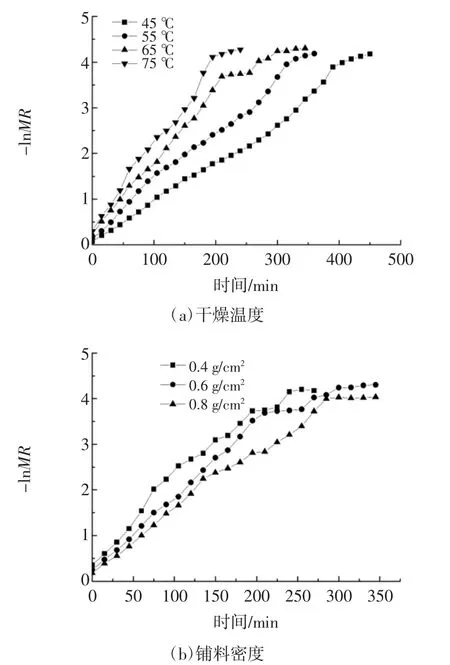
图6 不同条件蚕蛹热泵干燥过程-lnMR-t曲线Fig.6 -lnMR and t of silkworm pupa heat pump drying process under different conditions
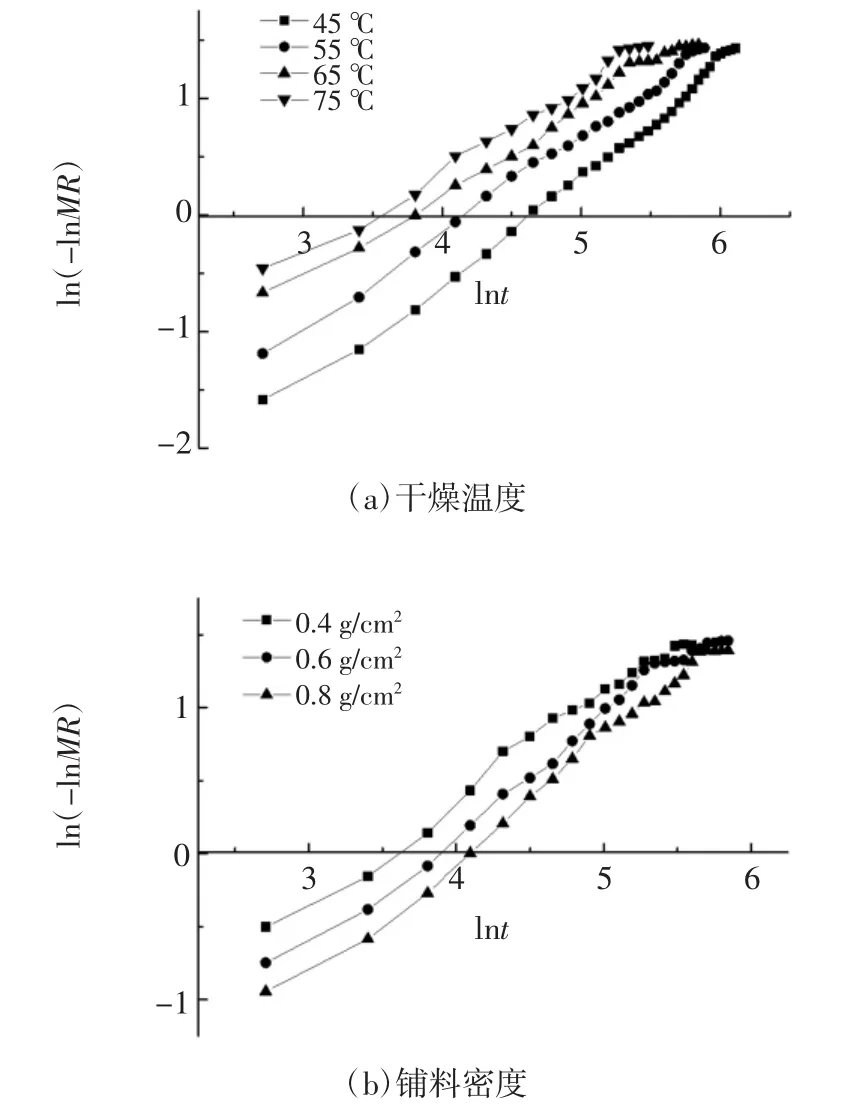
图7 不同条件蚕蛹热泵干燥过程ln(-lnMR)-lnt曲线Fig.7 ln(-lnMR)and lnt of silkworm pupa heat pump drying process under different conditions

式中:H 为铺料密度,g/cm2;L 为温度,℃;a、b、c、d、e、f为待定系数,可得到:
ln(-lnMR)=a+bH+cL+(d+eH+fL)lnt
通过软件SPSS19.0对试验数据进行拟合得到待定系数 a,b,c,d,e,f的数值为 a=-5.545,b=-2.024,c=0.059,d=1.034,e=0.259,f=-0.006。
得拟合方程为:

式中:k=e-5.545-2.024H+0.059L,n=1.034+0.259H-0.006L
该拟合方程 F=2 860.281,p<0.001,R2=0.990,表明该方程极显著且拟合度比较高。
2.2.3 动力学模型的检验
为了检验回归模型和试验数据的准确性,设置试验条件为铺料密度为0.8 g/cm2,干燥温度为45℃进行验证。拟合值和试验值结果见图8。
由图8可见,Page方程的试验值与拟合值对比得出二者拟合比较好,说明Page模型能够较好的反映和预测蚕蛹热泵干燥规律。
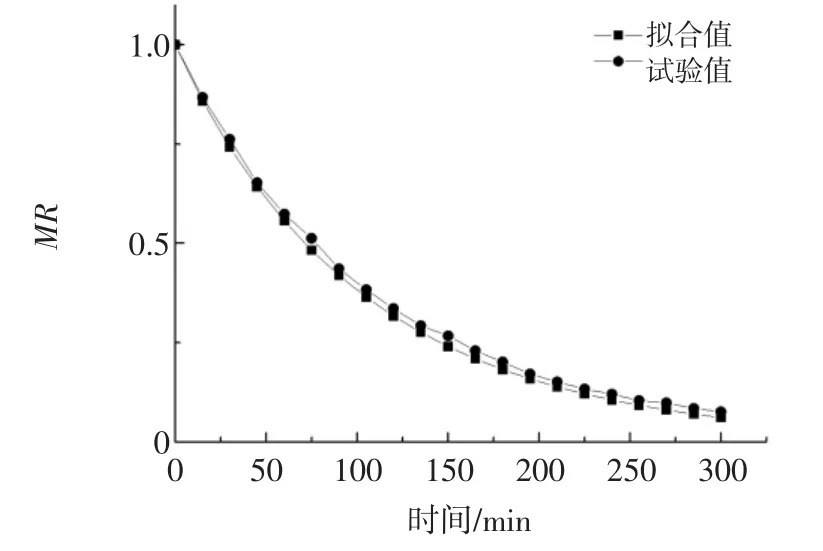
图8 蚕蛹热泵干燥的动力学模型检验曲线Fig.8 Test curve for kinetic model of the heat pump drying silkworm pupa
3 结论
1)本试验表明,干燥温度越高,铺料密度越小,蚕蛹干燥所需要的时间就越短,干燥速率越快,恒速期也就越不明显。蚕蛹的热泵干燥过程中主要存在加速、恒速和降速3个阶段,其中降速阶段占干燥过程中的大部分。
2)通过对5种常见的动力学模型拟合分析,确定蚕蛹热泵干燥特性符合Page模型,并通过用SPSS19.0软件对试验数据进行拟合,得到拟合方程为ln(-lnMR)=-5.545-2.024H+0.059L+ (1.034+0.259H-0.006L)lnt在试验条件范围内,Page模型的试验值与拟合值拟合比较好,能较好的反映蚕蛹的热泵干燥规律,且通过得出干燥温度、铺料密度的函数表达式和模型相关的参数,可以用来准确地预测到任意时刻蚕蛹水分比的含量。
