基于秋千法的带电作业入场位置确定方法研究

王磊，杨芳，谢龙光，浦石

（1.广东电网公司电力科学研究院，广州 510000； 2广东电网公司清远供电局， 清远 511500；3.北京拓维思科技有限公司，北京 100080）

引言

近几年来，随着用电需求的不断增加，各个电力系统的规模以及复杂程度也在不断提升。工业、农业用电以及生活用电的安全性以及稳定性也在逐年增加，这对我国电力系统的稳定性以及安全性带来了更大的挑战，现阶段确保供电的稳定运行成为电力系统的重要内容。

带电作业是保证公用电网供电持续性以及供电稳定性的一种作业方式，其中主要包含对高压电力电气装置的定期检查、维修以及相关设备的替换[1,2]等。电气设备长时间运行，需要对其定时进行测试、检查以及维修等，带电作业能够在不停电的情况对电气设备进行检修，同时为电网的安全稳定运行发挥了十分重要的作用。

随着电力系统检修体系的迅速发展，带电作业已经成为电力系统最为主要的作业方式。针对于带电作业入场位置确定的研究现阶段十分有限，并且现有方法也存在一定的弊端。针对以上问题，设计并提出基于秋千法的带电作业入场位置确定方法。仿真实验结果表明，所提方法能够有效降低运行时间，同时能够准确确定带电作业入场位置。

1 方法

1.1 最小距离计算

在计算区域没有确定边界的情况下，需要将无穷变设定为虚拟边界，同时将无穷边的边界条件设定为定解条件。在大多数情况下，场域是不存在边界的，但是形成它的源却存在边界，由此能够获取穷边的边界条件[3]，具体的计算式如下所示：

分析公式（1）可知，在无穷边的位置设定A代表一个有限量，则场函数是由边界确定的，与之对应的场函数u的取值为0。

均匀属于理想场，由此能够将其设定无穷变的边界条件，具体的计算式如下所示：

结合相关理论，需要将带电作业场地的连续域离散化成多个有限元的组合，通过有限元对部分距离[4,5]进行计算。

矩阵方程的表达式为：

式中：

[K]—系数矩阵；

[b]—不同节点的函数矩阵；

[f]—激励矩阵。

公式（3）为整体矩阵方程，通过公式（3）能够计算各个区域内不同函数的具体变化规律[6]，其中系数矩阵能够表示为以下的形式：

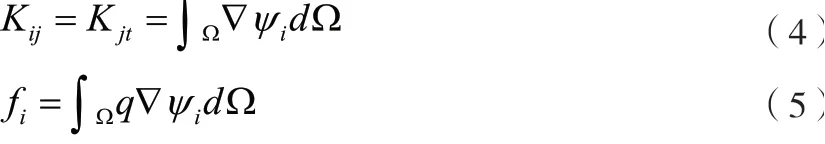
当q=0时，则fi=0。

假设相关待定系数的取值为节点处的函数数值，则矩阵方程能够表示为以下的计算式：

为了求解系数矩阵的相关操作步骤，需要分别计算出不同单元的结果后再继续进行叠加，假设利用N代表不同单元的数量，以下给出具体的计算方程：

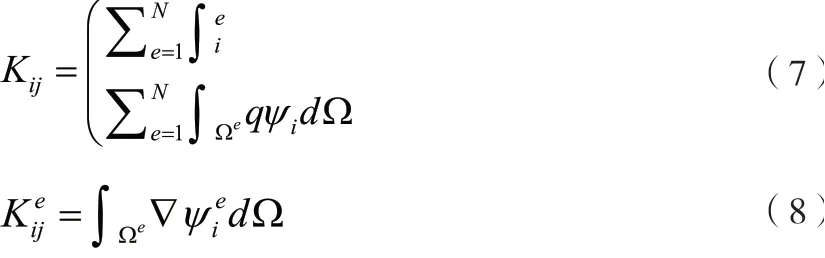
式中：

e—不同单元的量；

Ωe—对应单元的子区域；

综合分析上述计算式可知，系数矩阵能够划分成多个单一的局部系数矩阵；激励矩阵中的元素能够划分成不同子区间的积分取值[7]，以下给出具体的计算式：

不同的作业人员需要通过吊篮进入强电场，通过有限元方法对不同距离的电源数据进行采集以及计算。

其中多导体系统的总能量计算能够表示为以下的形式：

式中：

将公式（11）带入公式（12）中，则能够获取以下的计算式：

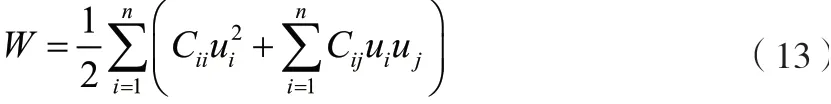
结合有限元分析方法，分别计算不同距离下带电作业人员的转移能量：

由于高压输电线路的电压等级十分高，在作业的过程中人体和导线之间的距离十分近，且人体的场强是十分强大的，需要通过屏蔽服务来确保作业人员的安全，其中屏蔽效率的计算式为：

式中：

U—屏蔽后的电压。

综合分析带电作业场地的实际情况，通过对应的计算方法获取带电体的点云数据，利用点云数据能够得到不同作业人员在各个位置到带电体的之间的最小距离[8]，具体的计算式如下所示：

1.2 基于秋千法的带电作业入场位置确定方法

在带电作业入场位置确定的研究中，需要通过秋千法计算坐标位置，以下给出具体的操作过程：

移动节点(x,y)接收到N个坐标，通过无线信号传播模型能够准确获取移动节点的距离[9]，同时能够获取坐标和第一距离以及第二距离之间的几何关系，具体的方程式如下：

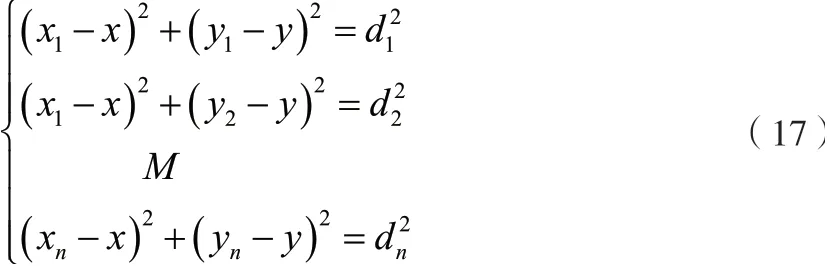
移动节点D的估计坐标计算式能够表示为：

其中：

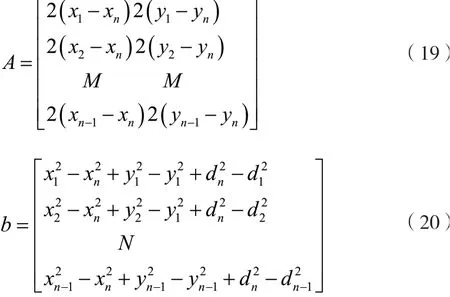
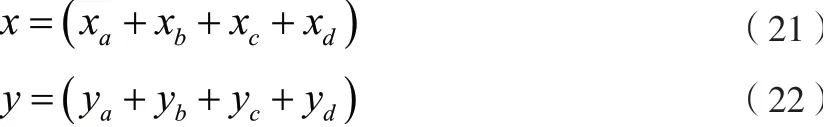
以下通过秋千法中的绝缘绳获取带电作业人员在相同预定位置的第一最小距离以及第二最小距离的距离和[10]，具体的计算式如下所示：

将公式（23）以及公式（24）展开，则能够获取以下的计算式：

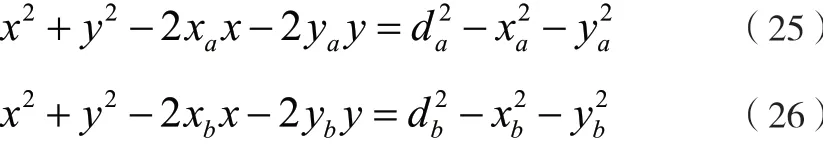
继续将公式（25）以及公式（26）展开，则能够获取以下的计算式：

其中：

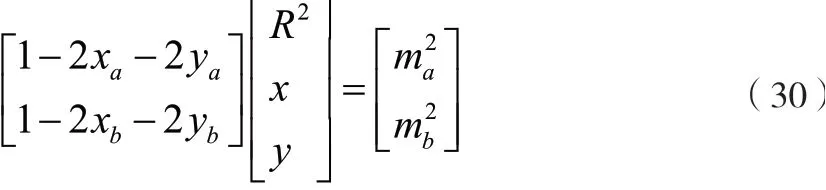
令公式（30）中的：

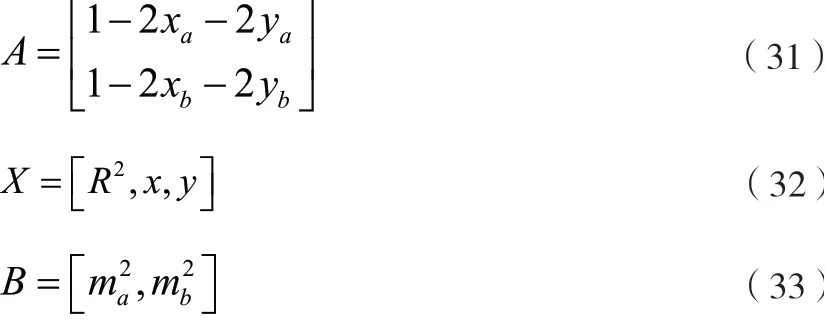
则以上公式能够转换为以下的形式：

引入改进的四点差分修正算法对测量误差进行修正，以获取准确的带电入场位置，具体的计算式如下所示：

2 仿真实验

为了验证所提基于秋千法的带电作业入场位置确定方法的综合有效性，需要进行仿真实验，实验环境为：CPU为PIV2.6 G，内存512 M，操作系统为Windows XP，编程环境为Matlab 6.0。

1）运行时间/（ms）：

以下分别对不同方法的运行时间进行比较，具体的对比结果如图1所示。

分析图1可知，所提方法能够有效减少运行时间，在节点距离不断增加的情况下，所提方法的运行时间依然保持相对稳定的状态，充分验证了所提方法的有效性，同时所提方法的操作过程简单，并且容易实现。

图1 不同节点距离下不同方法的运行时间对比结果

2）带电作业入场位置确定结果对比：

为了进一步验证所提方法的有效性，本文选取入场位置确定平均误差以及相对误差作为评价指标，两个指标的取值越低，则说明方法的带电作业入场位置确定结果越准确，以下分别给出不同方法的带电作业入场位置确定结果位结果，具体如表1～6所示。

综合分析表1～6的实验数据可知，随着节点距离的不断变化，文献[4]方法以及文献[5]方法的平均误差以及相对误差一直在增加，但是所提方法的平均误差以及相对误差则呈直线下降趋势，这充分说明所提能够更加准确的确定带电作业入场位置。

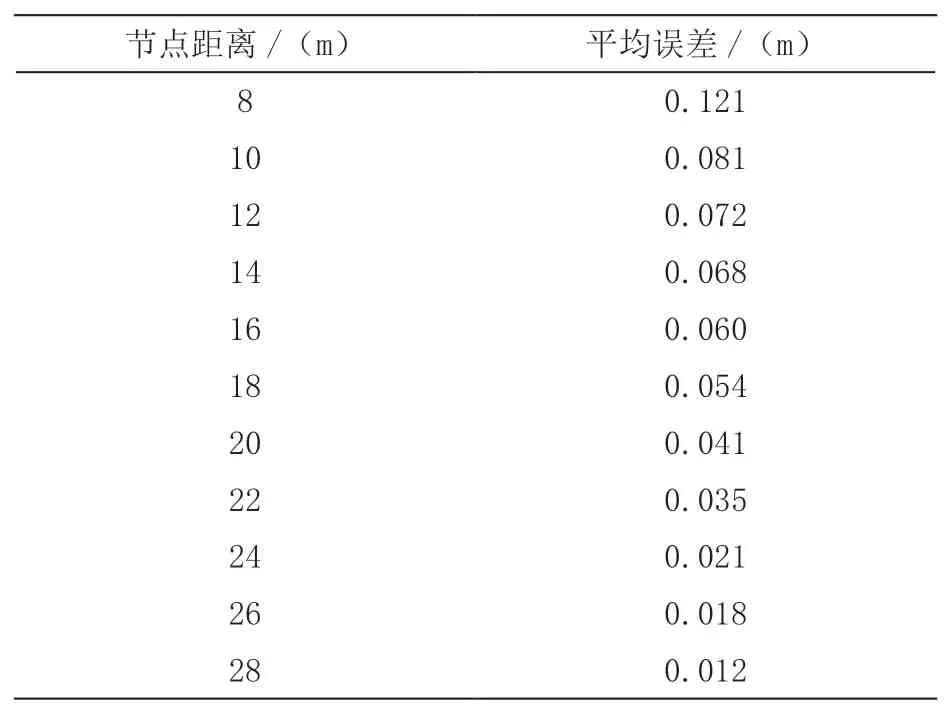
表1 所提方法的平均误差变化情况

表2 文献[4]方法的平均误差变化情况

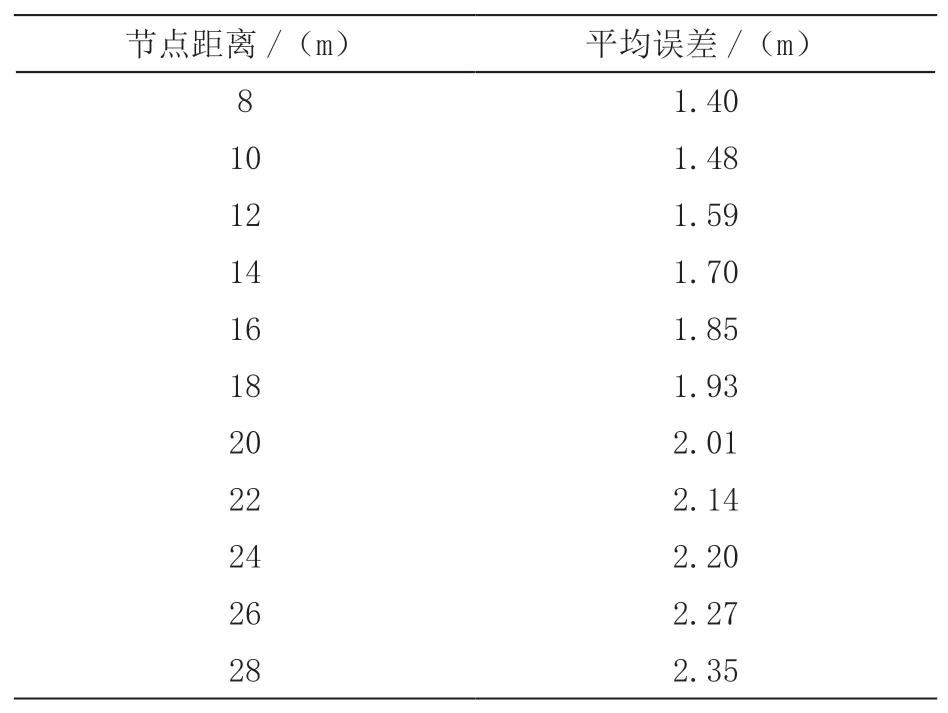
表3 文献[5]方法的平均误差变化情况

表4 所提方法的相对误差变化情况

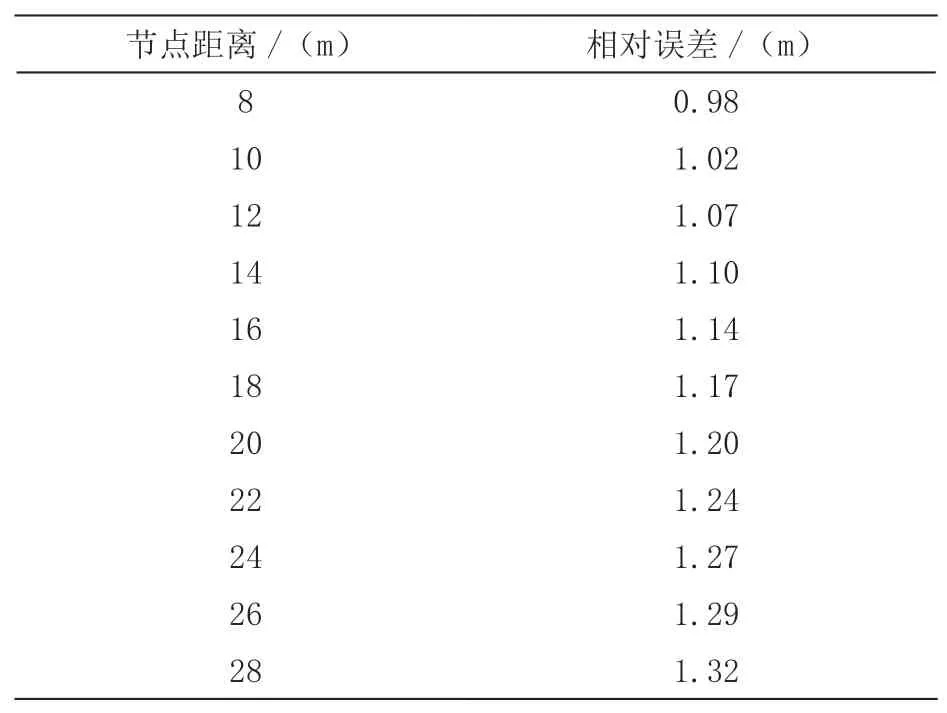
表5 文献[4]方法的相对误差变化情况

表6 文献[5]方法的相对误差变化情况

4 结束语

针对传统的带电作业入场位置确定方法存在的一系列问题，设计并提出基于秋千法的带电作业入场位置确定方法。仿真实验结果表明，所提方法能够有效降低运行时间，同时提升带电作业入场位置确定精度。