湿地湖泊相黏土应力-应变及屈服特性试验

朱 楠,张静娟,2,刘春原,2

(1.河北工业大学 土木与交通学院,天津 300401； 2.河北省土木工程技术研究中心,天津 300401)

湖泊湿地或古湖泊湿地在中国广泛分布[1]，由于气候变化及人类活动，大量的湖泊湿地干缩变小或消失.湿地湖泊相黏土由湖泊湿地或古湖泊湿地干缩形成，分布于湖泊湿地周边及古湖泊湿地遗迹地区，经历了湖泊湿地形成和扩张阶段的饱和湖相沉积，以及后期湖泊湿地干缩水位下降的陆相沉积，形成区别于海相软土的结构特征和工程特性[2].现有规范[3]对软基处理的要求主要针对海相软土制定.工程实践表明，若根据湿地湖泊相黏土较好的物理力学指标而不做地基处理，在施工后期或运营阶段会出现过大的沉降，造成工程事故；若直接套用海相软土的处理方法进行地基加固，又会出现过度加固的问题，造成浪费.

研究不同应力路径下天然沉积黏土的应力-应变特性和屈服特性能够帮助了解土体在实际工程中不同应力状态下的力学特性，并为土体本构模型的建立提供试验依据，目前主要通过室内应力路径试验进行相关研究.殷杰等[4-5]采用应力路径试验研究了连云港软黏土和张家港天然沉积粉质黏土的应力-应变关系和屈服特性.曾玲玲等[6-8]以广州南沙软土和连云港软土为对象，通过应力路径试验研究了固结方式、剪切方式和应力比对软土不排水剪切应力-应变特性和抗剪强度特性的影响.陈林靖等[9]对福州软土进行一系列卸载-加载应力路径试验，研究了不同固结条件下软土的卸载-加载应力-应变特征.李校兵等[10]通过应力路径试验研究了温州软土的应力-应变关系及强度特性.

天然沉积土往往具有一定的结构性，结构性使天然沉积土的力学性质与重塑土有显著区别[11].早期的研究主要针对结构性对土的压缩特性和剪切强度的影响展开[12-13]，随着研究的深入，近年来学者们已经开展不同应力路径下结构性对土体力学性质的影响及结构性演化规律的研究[14-15].目前，天然沉积黏土的应力路径试验研究及考虑结构性影响的应力路径试验研究，其研究对象主要为沿海发达地区的海相软土，对于海相软土应力-应变特性、屈服特性及结构性影响的研究已经取得较多成果，研究较为成熟，但对于内陆平原湖泊湿地干缩地区的湿地湖泊相黏土，尚未有相关研究报道.

本文从衡水湖附近的某高速工程现场取得湿地湖泊相黏土原状土样，分别对原状样和重塑样进行8个代表性路径的应力路径三轴试验，研究结构性和应力路径对湿地湖泊相黏土应力-应变关系的影响，并对结构性和各向异性影响下湿地湖泊相黏土的屈服特性进行系统研究.研究成果可指导相关地区工程建设，并为建立湿地湖泊相黏土本构模型提供依据.

1 试验概况

1.1 土的基本性质

湿地湖泊相黏土主要分布于湖泊湿地周边及古湖泊遗迹地区，厚度一般为3～8 m，上覆1～8 m冲积形成的粉土和粉砂薄层，下部为深厚的粉土和粉砂层，黏土在水平向呈连续分布，在地层纵向上呈成层分布，同一土层土质较均匀.原状土样取自衡水湖旁某高速工程现场，该区域土体具有自西北向东南由粗变细、自上而下由细变粗的规律，湿地湖泊相黏土层的含水率、孔隙比和压缩系数随深度增加呈减小趋势，取样位置为埋深5 m处土层，该处土层土质较均匀，取样具有代表性.湿地湖泊相黏土多为褐色、褐黄色，部分路段有灰色、灰黑色黏土，土样呈可塑、软塑状态.湿地湖泊相黏土的基本物理力学指标见表1，天然含水率ω超过35%，孔隙比e大于1.0，土样的物理指标较差，接近或达到软土标准，但天然含水率ω小于液限ωL，且液性指数IL小于1.0.同时土的力学性质较好，其压缩系数av1-2、压缩模量Es1-2、内摩擦角φ和黏聚力c也高于一般软土.

表1 湿地湖泊相黏土的基本物理力学性质

1.2 湿地湖泊相黏土的结构特性

湿地湖泊相黏土的固结压缩曲线见图1，采用R. Butterfield双对数压缩曲线法[16]确定土体的结构屈服应力为σy=107.89 kPa，而土体的上覆压力pc=88 kPa，两者之比为1.23.另外，根据无侧限抗压强度试验结果，湿地湖泊相黏土的灵敏度为4.1，属于中高灵敏性土，上述结果表明湿地湖泊相黏土具有明显的结构性.

Jiang等[17-18]的研究表明，不同荷载作用下，原状土与重塑土强度和变形特性的差异，主要由土体颗粒的胶结联结和孔隙比及孔径分布导致，即由胶结和组构所决定.在加载的不同阶段，土体胶结联结的破损程度、孔隙大小和孔径分布的变化情况，决定了土体的变形特性及强度大小.

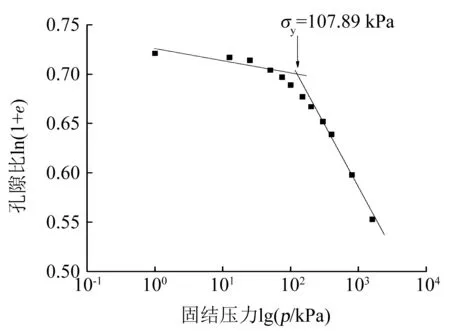
图1 湿地湖泊相黏土双对数压缩曲线

湿地湖泊相黏土的微观结构见图2(a)所示，湿地湖泊相黏土为片状大颗粒和土团粒相互依靠、搭接形成的叠片状和团粒状混合结构，颗粒之间和团粒之间存在胶结联结，表明土体具有明显胶结特性.在三轴试验剪切后(图2(b)所示)，土体发生结构屈服破坏，片状大颗粒和土团粒被压碎，胶结联结破坏，孔隙受到压缩，破碎的小颗粒在荷载作用下重新集聚成土团粒，形成新的结构.上述结果表明，当应力水平超过湿地湖泊相黏土的结构屈服应力后，土体发生结构屈服破坏，土体的胶结和组构发生相应改变，进而影响土体的强度和变形特性.

1.3 试验方案

采用英国GDS应力路径三轴试验仪，分别对原状土样和重塑土样进行8个代表性路径的应力路径三轴试验.由K0固结试验得到土的静止侧压力系数K0=0.49，结合土样埋深5 m处的竖向有效应力，计算得到土样的原位应力状态为p′=57.29 kPa，q=44.96 kPa.应力路径试验加载方案见表2和图3.

图2 湿地湖泊相黏土结构屈服前后微结构的变化

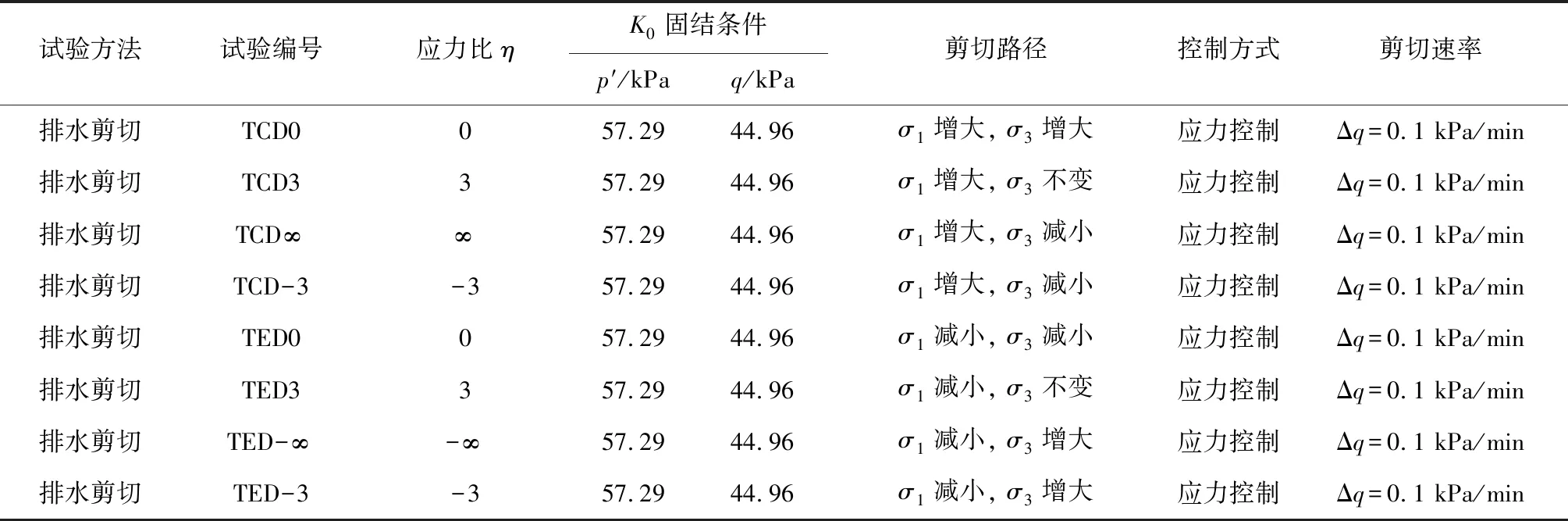
表2 应力路径试验方案

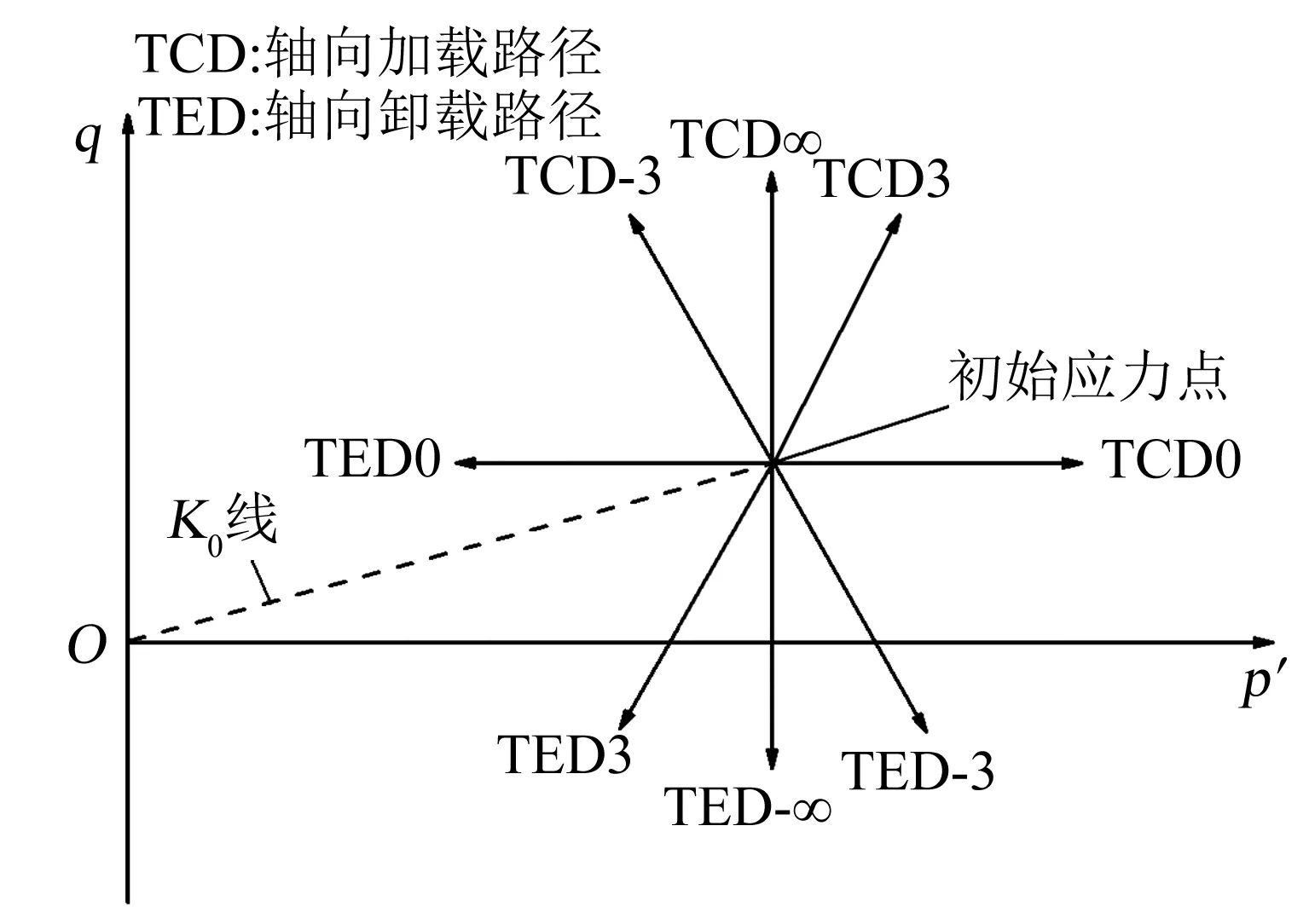
图3 不同应力路径的试验加载方案

2 试验结果分析

2.1 湿地湖泊相黏土与海相软土结构特性对比

图4为结构性对湿地湖泊相黏土[19]与温州软土[20]不排水剪切应力-应变特性影响的对比，可见湿地湖泊相黏土的结构强度较高，在围压150 kPa固结后仍有明显的结构性，原状土的q-εa曲线呈现软化特征，剪切过程中原状土的偏应力始终大于重塑土，直至剪切时土的结构屈服破坏，结构性影响逐渐消失，土体的q-εa曲线才逐渐趋近于重塑土.而温州软土结构强度较低，在围压150 kPa固结后土体结构损伤破坏，q-εa曲线呈现一定的硬化特征，在剪切初期原状土q-εa曲线与重塑土接近，在剪切后期，重塑土由于硬化作用剪切强度提高，偏应力大于原状土，而原状土的偏应力增长逐渐稳定.

上述分析表明，湿地湖泊相黏土具有明显的结构性，结构强度高于海相软土，在应力水平较高时才发生结构屈服破坏，应力-应变曲线呈软化特征，而海相软土结构强度较低，在低应力水平下即发生结构屈服破坏，应力-应变曲线呈现一定的硬化特征.

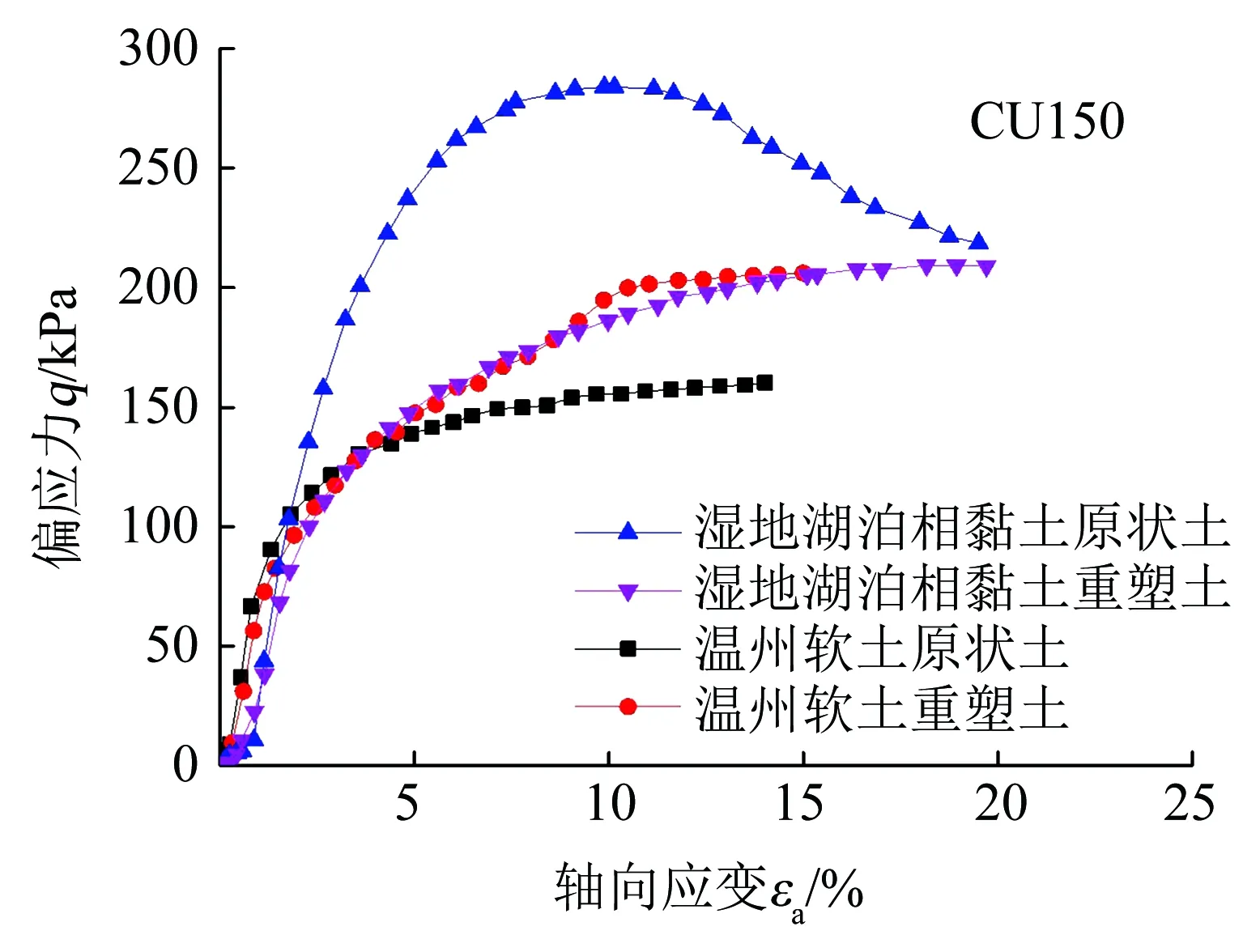
图4 结构性对不排水应力-应变特性影响对比[19-20]

2.2 结构性对应力-应变关系的影响

图5～7为湿地湖泊相黏土8个代表性应力路径的p′-εv曲线、q-εs曲线和εs-εv曲线.不同应力路径下湿地湖泊相黏土p′-εv曲线见图5，除等p′纯剪路径(TCD∞和TED-∞)外，其他应力路径的体积应变εv均随球应力增量Δp′的发展明显变化.当土体球应力增量Δp′>0时，在土的结构破坏前，原状土的抗压强度大于重塑土，并且压缩变形更小；当土体球应力增量Δp′<0时，原状土承担拉应力的能力高于重塑土，且最终的膨胀变形更大.等p′纯剪路径的球应力增量Δp′变化较小，基本呈水平向发展，但p′-εv曲线略有偏移.

分析可知，由于原状土具有结构性(胶结+组构)，胶结和组构能够共同承担压力并抵抗压缩变形，因此，在球应力增量Δp′>0的应力路径中，原状土抗压强度更高且压缩变形更小；在球应力增量Δp′<0的应力路径中，由于组构无法承受拉应力，荷载主要由胶结承担，并且胶结具有一定的延性，因此，当球应力增量Δp′<0时，原状土承担拉应力的能力更好且膨胀变形更大.

图6为不同应力路径下湿地湖泊相黏土的q-εs曲线.对于三向等压(TCD0)和三向等拉(TED0)路径，原状土与重塑土的偏应力q基本不变，但仍有剪切应变εs产生，并且原状土的剪切变形大于重塑土.当土体处于轴向加载路径(TCD3、TCD∞和TCD-3)时，原状土的q-εs曲线呈明显应变软化或理想弹塑性性质，在土的结构屈服破坏前，原状土的剪切强度高于重塑土；当土体处于轴向卸载路径(TED3、TED∞和TED-3)时，原状土与重塑土的q-εs曲线特征相似，原状土对负偏应力的承载能力略低于重塑土.

图5 不同路径下湿地湖泊相黏土的p′-εv曲线

分析可知，轴向加载条件下，由于原状土的胶结和组构能够共同承担偏应力，提高了土体的剪切强度，直到土的结构屈服破坏前原状土的剪切强度高于重塑土.而在轴向卸载条件下，原状土的组构不再承担偏应力，仅由胶结承担荷载，由于原状土骨架主要由颗粒间的胶结固定，在胶结破坏后，土颗粒很快进入滑动调整状态，因而在剪切过程中原状土承受的负偏应力小于重塑土，且在剪切后期趋近于重塑土.

图7为不同应力路径下试样的εs-εv曲线，可见当土体处于体积压缩Δεv>0的路径时，在相同剪切应变εs下原状土的体积应变εv小于重塑土；而在土体处于体积膨胀Δεv<0的路径时，相同剪应变εs下，原状土的膨胀变形εv也等于或大于重塑土.

分析可知，当土体受压体积压缩时，原状土具有的胶结和组构能够共同作用帮助土体抵抗压缩变形，因而在剪切过程中原状土的压缩变形小于重塑土.但当土体受拉体积膨胀时，由于土的组构无法承受拉应力，仅由胶结承担，并且胶结具有一定的延性能产生拉伸变形，因此，在剪切时原状土的膨胀变形大于重塑土.

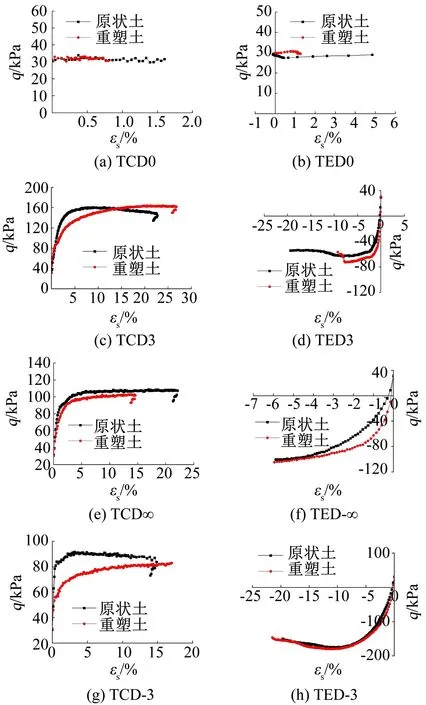
图6 不同路径下湿地湖泊相黏土的q-εs曲线

分析图5～7可知，对于三向等压路径TCD0和三向等拉路径TED0，原状土除体积应变外仍有剪切应变产生；对于等p′纯剪路径TCD∞和TED-∞而言，除剪切应变外试样仍有体积应变产生.这表明球应力和偏应力之间存在交互影响，无论是三向等压路径、三向等拉路径还是纯剪路径，不同应力路径下土体都同时受到球应力和偏应力的共同影响，这与文献[5]中的规律一致.对比图3和7可知，由于原状土的球应力和偏应力存在交互影响，不同应力路径下试样的应变εs-εv曲线方向与应力路径q-p′曲线方向并不完全一致.

2.3 各向异性对屈服轨迹的影响

q=σ1-σ3.

(1)

则|q|=|-q|可表示为

σ1-σ3=-(σ1-σ3).

(2)

进而有

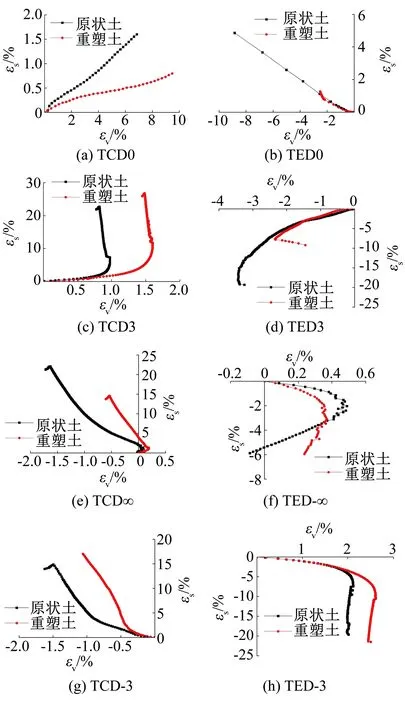
图7 不同路径下湿地湖泊相黏土的εs-εv曲线

σ1=σ3.

(3)

重塑土的竖向应力与径向应力相等，具有各向同性性质.由制样过程分析可知，重塑土在制样过程中胶结和初始组构完全破坏，结构性和各向异性丧失，因此，可视为均质的各向同性材料.

由图8可知，原状土的初始屈服点轨迹呈旋转的椭圆形，屈服轨迹上p′相同的两点纵坐标q不等，即|q|≠|-q|.由于湿地湖泊相黏土在沉积过程中

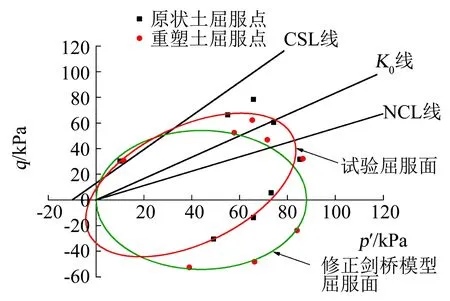
图8 原状土与重塑土的屈服轨迹

受到K0固结作用，导致土体在竖向和径向力学性质存在差异，因而具有各向异性性质.

针对目前我国农村水利的立法工作相当滞后的状况，应在近期的水利立法工作中将农田水利法、农村供水条例列为重点项目，尽快颁布施行；应加快制订节水灌溉补偿及激励办法等法规；同时加快编制县级农田水利建设规划，尽快将农田水利基础设施建设和管理、农村供水工程的建设和管理纳入法制化和依据规划管理的轨道。

2.4 湿地湖泊相黏土的屈服特性

2.4.1 屈服面的对比

湿地湖泊相黏土与海相软土屈服面对比见图9，各类土体的初始屈服轨迹均呈旋转的椭圆形.其中，连云港软土屈服面小于湿地湖泊相黏土，杭州软土、温州软土和上海软土屈服面大小和旋转角度与湿地湖泊相黏土接近，但各类软土屈服面均经过q-p′平面原点，且临界状态线CSL也均从q-p′平面原点出发.

湿地湖泊相黏土特殊的沉积环境和沉积历史，导致其工程特性与海相软土有着显著区别[2].受沉积时的K0固结状态影响，湿地湖泊相黏土屈服轨迹的旋转角度与其他软土有一定偏差；同时，由于胶结对湿地湖泊相黏土有明显的影响，其临界状态线CSL和初始屈服轨迹不经过q-p′平面原点，而是在q-p′平面原点左侧与p′轴相交[19]，这一点与其他海相软土明显不同.

2.4.2 屈服轨迹特征

由图8可知，原状土初始屈服轨迹呈旋转椭圆形，而重塑土初始屈服轨迹近似为以p′轴为对称轴的椭圆形，与修正剑桥模型屈服面形状相似，因此，首先采用修正剑桥模型对重塑土屈服轨迹进行拟合.

修正剑桥模型屈服面方程为

(4)

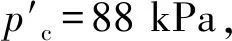
天然沉积黏土由于K0固结的影响具有各向异性性质[4-5,21-26]，其屈服面形状在q-p′平面呈现旋转的椭圆形.为了正确描述天然沉积黏土的各向异性特征，学者们尝试通过旋转修正剑桥模型的屈服面来描述天然沉积土旋转的屈服轨迹，其中具有代表性的有Nakano[25]和Wheeler等[26]提出的各向异性模型.

Nakano等将修正剑桥模型的屈服面旋转为以K0线为对称轴的椭圆形屈服面，认为K0线与NCL线是重合的，即认为ηNCL=ηK0，以K0线的斜率ηK0作为描述各向异性影响的参量引入修正剑桥模型的屈服面方程中，其屈服面方程为

(5)

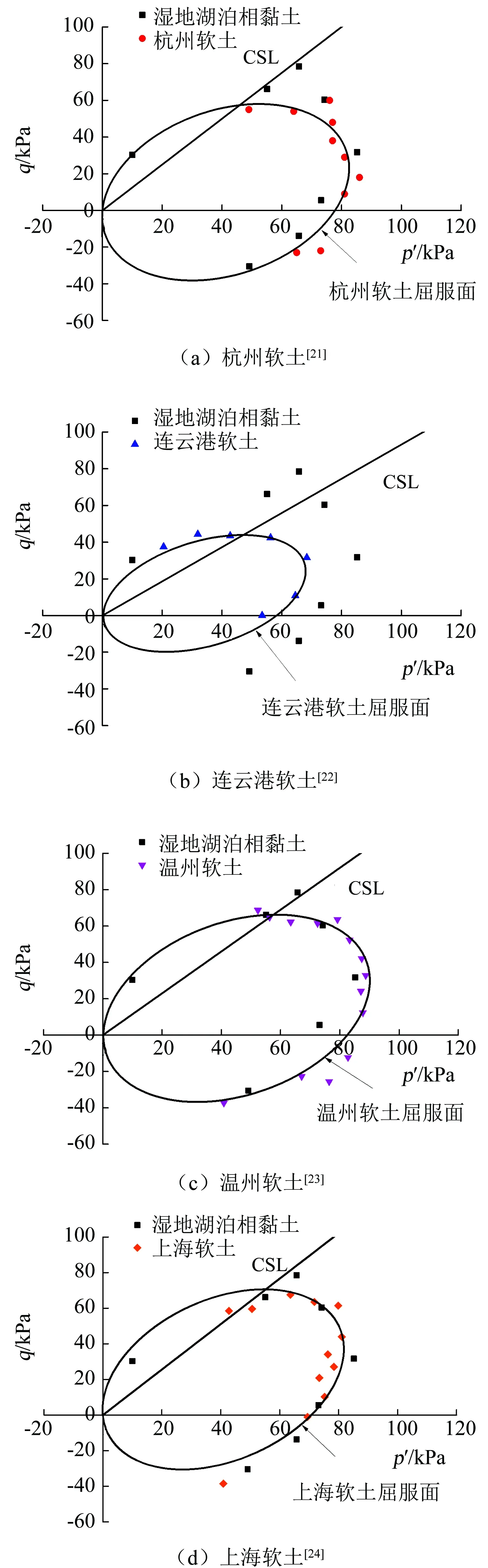
图9 湿地湖泊相黏土与海相软土屈服面对比

此外，Wheeler也提出了一种旋转修正剑桥模型椭圆屈服面的方法，认为原状土旋转后的屈服面应以NCL线为对称轴，且NCL线与K0线之间存在一定夹角，二者斜率ηNCL和ηK0之间的关系可表示为

(6)

以NCL线的斜率ηNCL作为描述原状土各向异性的参量，将其引入到修正剑桥模型椭圆形屈服面方程中，得到Wheeler模型的屈服函数为

(7)

将Nakano模型和Wheeler模型的屈服面同湿地湖泊相黏土的屈服轨迹进行对比(见图10)，发现Wheeler模型的屈服面比修正剑桥模型和Nakano模型能更好地描述湿地湖泊相黏土的初始屈服轨迹，但由于各模型屈服面均经过q-p′平面原点，与试验屈服轨迹之间仍有一定偏差.

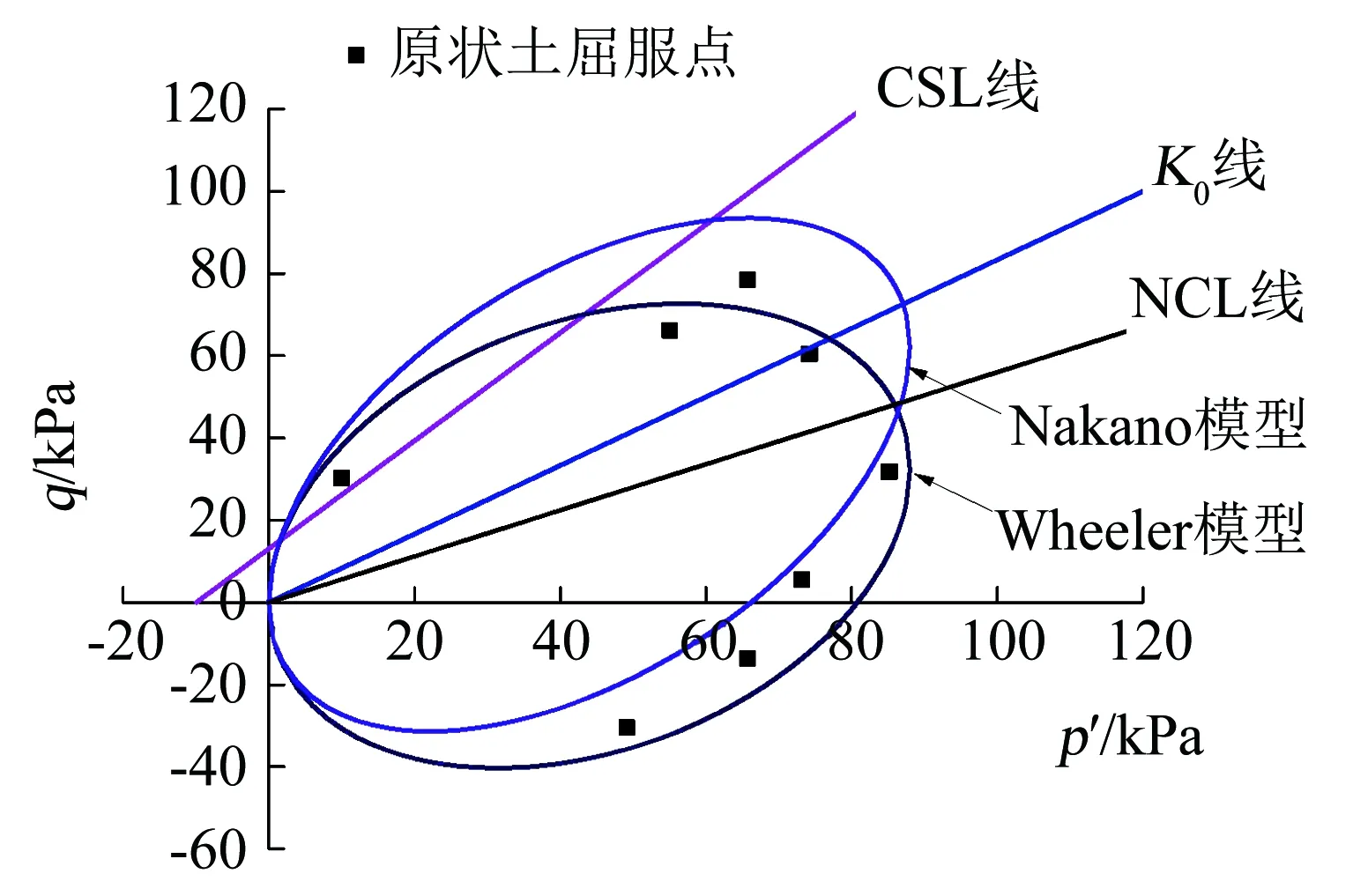
图10 湿地湖泊相黏土屈服轨迹与其他本构模型屈服面对比

许多学者的研究发现[27-29]，结构性土中普遍存在胶结的影响，胶结的存在使结构性土能够承受一定的拉应力，使得结构性土的CSL和初始结构屈服面都与p′轴相交于q-p′平面原点左侧，CSL与q轴有一定的截距C，因此,在描述结构性土的屈服面时，应考虑胶结引起屈服面平移.由图10可知，湿地湖泊相黏土的屈服轨迹左端点位于q-p′平面原点左侧，因此,需要考虑胶结对屈服轨迹的影响.

2.4.3 屈服轨迹的验证

为验证湿地湖泊相黏土屈服轨迹的正确性，同时解释湿地湖泊相黏土的屈服和破坏规律，采用固结不排水三轴剪切试验来验证试验得到的屈服轨迹.

湿地湖泊相黏土原状土固结不排水三轴试验的应力路径与屈服轨迹见图11[19]，原状土的固结不排水应力路径在应力(p′，q)约为(59 kPa，66 kPa)处达到屈服，在屈服后随剪切应变继续增加，原状土偏应力q增长趋势减慢，最终在应力达到CSL后发生破坏.经固结不排水三轴试验的验证表明，由应力路径试验得到的湿地湖泊相黏土屈服轨迹较为符合实际，能够比较合理地反映湿地湖泊相黏土的屈服和破坏特性.

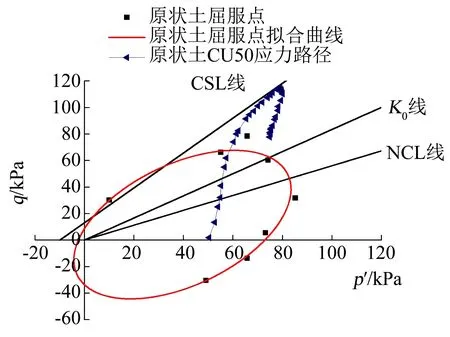
图11 三轴不排水剪切应力路径与屈服轨迹关系

2.4.4 塑性流动特性

当原状土达到屈服状态后，土体在屈服后的应变以塑性应变为主，弹性应变可忽略不计，因此，采用屈服后土体的应变增量方向作为该路径下试样屈服后的塑性应变增量方向.在判断塑性应变增量方向时，取约1%大小的塑性应变进行判断，这样既不会因为数据量较少过分离散，又不会因为塑性应变过大影响对塑性应变增量方向的判断[4].

以逆时针为正，判断在各应力路径的屈服点处塑性应变增量方向与该点处屈服轨迹法线方向的夹角.湿地湖泊相黏土塑性应变增量与屈服轨迹法线的关系和夹角如图12和表3所示.可以看出，除了TED3路径的塑性应变增量方向与屈服轨迹法线夹角为39.6°外，其他路径塑性应变增量方向与屈服轨迹法线的夹角均在0～24°，可近似认为湿地湖泊相黏土的塑性应变增量与屈服轨迹的正交性较好，在建立本构模型时可以采用相关联流动法则.

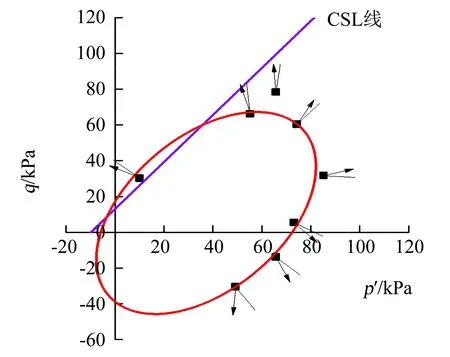
图12 屈服后湿地湖泊相黏土的塑性流动方向

湿地湖泊相黏土塑性流动特性的分析表明，尽管土体的应力路径q-p′与应变方向εs-εv受球应力和偏应力的交互影响而存在偏差，但其屈服后的塑性应变方向始终与应力增量的方向存在一致性.因为结构性土的塑性应变主要由土体结构屈服破坏后土颗粒不可恢复的滑动调整产生，在大主应力方向上土体的结构破坏趋势会更明显，而土颗粒的滑动调整也更为剧烈，该方向的塑性应变会更为显著，因此湿地湖泊相黏土屈服后的塑性应变与屈服轨迹的正交性较好.

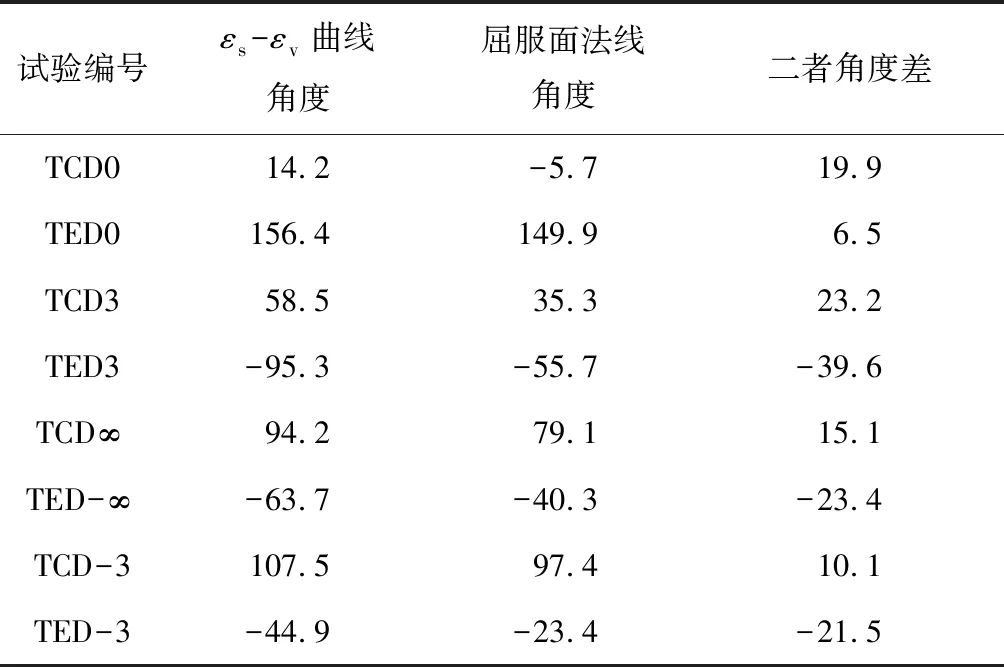
表3 湿地湖泊相黏土εs-εv曲线方向与屈服轨迹法线方向对比

3 结 论

1)湿地湖泊相黏土的应力-应变特性受到胶结和组构的显著影响，由于不同应力路径下湿地湖泊相黏土均受到球应力和偏应力的交互影响，一方面是应变方向与应力路径方向存在一定偏差，另一方面塑性应变增量与屈服轨迹却存在较好的正交性.

2)湿地湖泊相黏土的应力-应变特性受到结构性(胶结和组构)的显著影响.当土体球应力增量Δp′>0产生体积压缩时，胶结和组构共同承担荷载，使原状土的抗压强度更高，压缩变形更小；当土体球应力增量Δp′>0产生体积膨胀时，土体的组构不能承拉应力，只有胶结承担荷载，使原状土比重塑土的承载力更高，膨胀变形更大.

3)不同应力路径下湿地湖泊相黏土都同时受到球应力和偏应力的交互影响，试样的应变曲线方向与应力路径方向并不完全一致，但塑性应变增量与屈服轨迹的正交性较好，在建立本构模型时可以采用相关联流动法则.

4)受到沉积时K0固结和胶结的影响，湿地湖泊相黏土的屈服轨迹与其他海相软土相比存在显著差异.湿地湖泊相黏土的屈服轨迹为一旋转椭圆形，大致以NCL线为对称轴，并且CSL线和屈服轨迹不经过q-p′平面原点，而是与p′轴相交于q-p′平面原点左侧.

湿地湖泊相黏土固结不排水三轴试验的验证表明，试验屈服轨迹能够比较合理地反映湿地湖泊相黏土的屈服特性.可以采用修正剑桥模型为基础，考虑屈服面的旋转和平移来建立湿地湖泊相黏土结构性和各向异性本构模型.