人力资本要素与企业创新绩效——基于上海科技企业的实证研究

裴 政，罗守贵，2

（1.上海交通大学 安泰经济与管理学院，上海 200030；2.上海交通大学 中国城市治理研究院，上海 200030）

人力资本对企业创新的促进作用已被大多数学者认同。不同理论视角考察人力资本在企业创新中的作用时的落脚点不尽相同。在人力资本的计量上，众多文献选择人力资本某一方面进行研究，少有文献对人力资本的各个要素进行全面的分解与度量。本文以完备的分解方式，将总人力资本划分为数量特征、质量特征以及结构特征等多个要素，并通过学历差异、职称差异两种方式衡量不同角度的人力资本质量差异，考察各要素对创新绩效的影响。本文认为人力资本的数量、质量与结构可通过不同的作用机制对创新绩效产生影响。人力资本的数量特征是对人力资本“规模效应”的一种度量，隐含了研发人员个体作用的同质性假设，这也是一般理论模型对创新人员这一变量的简化表达，即仅采用创新人员人数指代创新人力资本投入；人力资本质量特征假设不同研发个体作用不同，研究研发人员创新绩效的“偏态分布”，在这种情况下，人力资本的“规模效应”可能不再明显，而会出现诸如“明星科学家（star scientist）”的效应，即少部分人决定创新过程与创新绩效；人力资本结构特征是指创新部门和非创新部门的比例，表征了研发、生产与后勤的人力配比，是对创新部门的“规模效应”与公司组织结构的衡量。

人力资本通常分为通用型和企业专用型两类，故本文采用学历与职称衡量人力资本质量差异，将其分解为学历差异与职称差异。研发人员的学历一般形成于工作之外（或之前），衡量标准为研发人员的学习能力、通用知识与技能的掌握；而研发人员的职称来自长期工作积累与工作成果的转化，衡量标准为研发人员对该行业经验、专用知识与技能的掌握［1-3］。通过比较人力资本的学历差异与职称差异对创新绩效的影响，可以分析通用型和专用型的人力资本对企业创新绩效的不同影响。

资源基础观（resource-based view）认为，人力资本是企业的内在资源，为创新提供着用之不竭的动力。但这一观点有一定的局限性，ROTHAERMEL和HESS［4］将企业创新的影响因素分成个人层次、企业属性以及创新网络3个层次，而根据FELIN和FOSS［5］、DANSEREAUN等［6］、KLEIN 等［7］的研究，仅在单一层次考察人力资本的作用存在对不同层次要素同质性、独立性的过强假设，因此在对某一层次的要素进行研究时，必须要考虑或控制其他层次要素的交互影响。因此，本文在考察人力资本的同时，也控制了创新网络变量及其与人力资本的交互作用。

本文采用上海市1 585家企业的5年跟踪数据，度量了上海市科技企业的人力资本总量及其分解后的数量、质量、结构三要素对企业创新的作用，并将人力资本质量要素分解为学历差异、职称差异，即衡量通用型与专用型的人力资本质量差异对企业创新绩效的不同影响，此外，还进一步探究了企业按照行业、规模分类后各要素作用的变化情况。

研究发现，人力资本的数量、质量、结构要素都对创新绩效有正向影响，在全样本中数量及结构两个要素的贡献更显著，但在子样本中的结论则表现不同。首先，大企业相较小企业、制造业相较服务业，均有更明显的人力资本“规模效应”。其次，不同规模、行业的企业人力资本的质量差异虽均对创新绩效产生影响，但因其作用方式与机制不同，导致通用和专用型人力资本对不同类型的创新过程作用效果不同。大企业、制造业存在更高比例的渐进式过程创新，需要专用型的人力资本，因此职称差异是人力资本质量差异的主要因素；而小企业、服务业则有更多的突破式产品创新，需要通用型的人力资本，学历差异将会对创新绩效产生更明显的作用。

1 文献综述

NELSON和PHELPS［8］最早论证了人力资本对创新的作用机制。此后，LUCAS［9］定义了专业人力资本，指出其诞生于生产实践中，并对创新有重要作用；BAUMOL［10］提出了人才配置与创新绩效关系的相关理论，认为长期经济增长的稳态差异主要来自人力资源差异导致的创新效率差异。其他理论文献也倾向于将人力资本作为创新的核心变量，GRILICHES［11］提出创新是人力资本、物质资本以及创新效率（剩余）的函数，HITT等［12］认为企业的创新表现至少应该是以人力资本为变量的某个函数。

人力资本在企业层面对创新的影响是多层次的。人力资本的积累与人力结构的配置将共同作用于创新［13-15］，且人力资本的作用会随着其他创新要素的投入不同而变化。但多数文献对人力资本计量与考察并不全面。对于人力资本的数量特征，杨勇和达庆利［16］、何庆丰等［17］、李柏洲等［18］、朱承亮等［19］采用创新人员数量为指示变量；MARVEL和LUMPKIN［20］、LÖÖF［21］、卢馨和黄顺［22］采用创新人员受教育年限加总这一变量，但从本质上仍是对人力资本数量特征的研究。对于人力资本质量特征，高素英等［23］、朱承亮等［19］、吴小立和廖东声［24］、王娟和王毅［25］、PARROTTA等［26］采用平均学历或学历占比度量人力资本质量；何庆丰等［17］、叶明确和杨亚娟［27］、曾德明等［28］、ANDRIES和CZARNITZKI［29］采用高级研究人员或高级职称占比度量人力资本质量；吴淑娥等［3］、ØSTERGAARDA等［30］，SUBRAMANIAN等［31］则采用上述两种方式衡量。对于人力资本结构，洪俊杰等［32］、卢馨［33］、张斌［34］均采用研发人员占全时人员比作为结构的衡量指标，并进行了详细讨论。

人力资本异质性与质量差异对创新绩效会产生显著影响，LOTKA［35］早在研究中指出人力资本创新绩效的“偏态分布”，统计结果表明在化工产品的创新中5%的研发人员大约贡献了全部创新成果的50%，ERNST等［36］也得出类似的结果。此外，胡凤玲和张敏［37］、ØSTERGAARD等［30］也指出人力资本的异质性和质量差异对企业创新有显著影响；ROTHAERMEL和HESS［4］发现少部分顶尖的创新人才主导了美国制药企业的创新过程，引申出“明星科学家”效应；ZUCKER等［38］最早在研究生物制药产业时提出该问题，STUART等［39］在后续的研究中发现，在生物医药领域，公司内部的创新人才发挥“看门人”的作用，有利于促进企业内部知识和外部知识的交互；LIEBESKIND等［40］认为企业内部的科学家对于评估企业所进行研究的质量和潜力至关重要，并且可以直接影响企业合作伙伴的选择；HESS和ROTHAERMEL［41］发现明星科学家存在于成熟产业链中的强势企业，并在产业链与知识整合中发挥巨大作用。

除了“明星科学家”效应，按照职称、学历划分的人力资本专用型与通用型差异也是人力资本质量差异的讨论重点。人力资本专用型理论来自资产专用性理论。吴淑娥等［3］针对西安高新企业的调研数据将人力资本按类型划分为创新人才（通用人才）及效率人才（专用人才），她认为创新人才具有全面的知识体系以及强大的创造动机，学历衡量了创新人员的研发能力、自学能力和知识惰性，因此可将学历作为衡量创新型人才的指示变量；而效率型人才依据经验学习，通过“干中学”获取知识，最终解决了企业的专用问题，因此可将职称作为衡量效率型人才的指示变量，并得出了“通用人才促进了产品创新绩效，专用人才虽抑制了产品创新绩效，但却促进了生产效率提高”的结论。吴爱华和苏敬勤［2］进一步深化了该问题，将专用人才与通用人才结合渐进式创新与突破式创新，认为拥有通用知识的通用人才更能在突破式创新中发挥作用，而拥有专用知识的专用人才更适合渐进式创新。ANDRIES与CZARNITZKI［29］认为，就小企业而言，基础研发人员对创新绩效展现出很强的促进作用，且这种作用和研发人员参与的创新类型相关，即相比于过程创新，基础研发人员更适合在产品创新中发挥作用。HERSTAD等［42］发现从高校、科研机构返聘的研发人员以及高学历的研发人员对企业技术突破创新有明显促进作用。ØSTERGAARDA等［30］、PARROTTA等［26］也指出以学历或职称来衡量人力资本质量存在显著差异。综上，本文认为以学历衡量人力资本质量差异可反映研发人员通用知识差异，与突破式创新更加相关，而以职称衡量人力资本质量差异可反映研发人员专用知识差异，与渐进式创新更加相关。但是，仅研究人力资本某一方面是片面的，有必要将人力资本划分为数量、质量、结构不同要素，并采用非数量（本文采用受教育年限）的方式对人力资本质量的差异进行描述。

此外，当视角聚焦到企业的创新网络时，人力资本依旧发挥着重要作用。首先，企业的属性（包括人力资本、R&D支出、吸收能力等）会影响创新网络对创新的效用发挥［43-44］。其次，专业化分工使得企业的人力资本等自主创新要素并不能满足企业的创新需求，当企业无法完全从内部获取资源时，就会寻求从外部获取资源，进而形成创新网络［45］。因此，异质性的人力资本是企业形成并需要创新网络的重要原因之一，在考虑企业之间创新网络的影响时，必须要考虑各企业人力资本的异质性与结构差异［5，46］。人力资本与创新网络之间存在正向的交互关系，因此在研究中必须要控制创新网络及其交互作用。

2 数据和变量

2.1 数据来源

自2008年起，上海市科学技术委员会按年度开展科技企业统计工作，其编制的年报内容包括企业研发投入（资金、人员等）、创新绩效（专利申请、专利授权等创新成果）、经济联系（政企、企业创新合作）和经济产出的情况，其中包括极具价值的研发人员描述及企业创新合作伙伴的统计指标。鉴于本研究目标及数据的可得性，本文采用2011—2015年的平衡短面板数据，剔除异常值后，最终样本量共7 925个（即1 585家企业5年的跟踪数据）。

选用该数据出于以下原因。①该数据具有较强的可信度。数据由官方在年度科技企业登记时一并完成统计，作为完成登记的硬性指标，因此整体质量及可信度较高，上海市科委对企业的调研问卷原则上与《上海市统计年鉴》中“主要年份科技型企业状况表”统计方式相同。②该数据具有一定的代表性。上海市作为中国经济与创新活动最活跃的地区，上海数据可以在一定程度上反映我国科技企业的创新过程，该样本涵盖了92个行业和所有经济属性，并包括上市及非上市企业，因此普适性及代表性强。③选择该数据贴近本文对科技企业创新绩效的研究，样本企业的年平均创新成果数为13件，平均研发人员数为92人，且该样本为上海市科委抽样选择，对科技企业有很强的代表性。

由于2015年以后上海市科委的统计数据口径发生变化，无法形成有效的跟踪面板数据，因此本样本截止到2015年，在时效性上存在一定折扣。但根据上海市2011—2018年统计年鉴对上海市科技企业和规模以上工业企业的创新统计，上海市规模以上工业企业2010—2017年的创新投入及绩效始终保持稳定上升（年化复合增速6%）。对于科技型企业，2010—2017年企业平均申请专利数稳定在4.5件左右，平均从业人员和研发人员投入均保持稳定上升，未见2016年及2017年相较之前有较大趋势性变动。因此，本文的相关结论可以解释近8年来上海科技企业创新绩效持续增长的内在原因，且实证规律有一定时间维度上的普适性。

2.2 变量测量

本文沿用了之前文献［4，47-49］大多采用的企业创新成果数量来度量企业的创新产出，包括企业专利、软件著作权登记、集成电路布图设计登记以及其他创新成果登记。对于这些变量均采用申请或上报口径，以尽可能减少创新过程和成果之间的间隔［50］。尽管采用创新成果数量度量创新绩效有一定的缺陷，但本文认为采用的变量是相对准确的指标：①此处教育年限按以下方法设定：本科学历16年，硕士19年，博士23年，并将非本科（专科及以下）的教育年限统一为12年（该部分在研发人员中占比极少）。为了避免专利的过高申请门槛，采用各种创新成果件数加总的方式，以求尽可能囊括全部创新成果；②由于样本选用上海市的研发企业，数据直接来自上海科委的企业调查，企业有较高的创新申报意愿，不太可能隐瞒创新成果。

通常来说，用货币计量人力资本主要有3种方式，即报酬折现法、人力资本加工成本法和未来折现法［51］。考虑数据可得及统计准确性，本文选用第2种方式，将研发人员所受教育作为人力资本加工成本的主要部分，通过受教育程度来衡量人力资本，即将企业中从事科技活动人员的受教育年限加总作为总的人力资本。对于研发人员，其所受的教育应该作为其人力资本形成的主要投入。为避免将教育年限简单的同质加总，本文采用舒尔茨教育年限法对不同教育年限①进行赋权加总，具体权重根据周晓和朱农［52］的研究中上海地区的测算结果。因此，本文中公司的总人力资本等于企业中从事科技活动人员的受教育年限的舒尔茨赋权加总。

本文尝试对总人力资本进行完备且独立的分解，即将总的人力资本分解成数量、质量和结构3个要素，并分别用研发人员总数、平均受教育年限（下文用平均人力资本指代）、研发人员占公司人员比例（下文用研发人员占比指代）衡量，而这3个要素的乘积即为总人力资本。值得注意的是，这里的平均人力资本是采用学历来衡量人力资本质量。在分解一中，可以通过观察研发人员总数与研发人员占公司人员比例的显著性来推断人力资本数量和结构对创新绩效的影响。

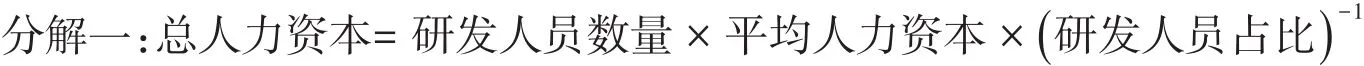
进一步将总人力资本分解成4个要素，并通过学历和职称两个维度衡量人力资本质量，即将研发人员人数分解为非高级职称研发人员人数和高级职称研发人员人数。将人力资本质量划分为专用型与通用型，可以更全面地刻画人力资本的质量差异，进一步提高分解的全面性和完备性。

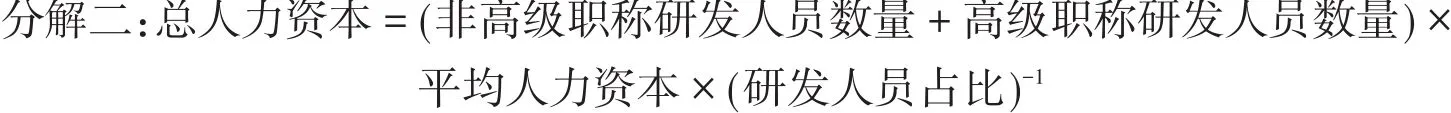
分解二在分解一的基础上增加了人力资本质量的两种衡量方式，可以通过观察高级职称与非高级职称研发人员人数对创新贡献的差异来判断研发人员创新绩效的“偏态分布”，以及以职称衡量的研发人员质量差异是否对创新绩效有影响，进而探究创新过程中的“明星科学家”效应。此外，可以通过观察平均人力资本对创新贡献的显著性来判断以学历衡量的研发人员质量差异是否对创新绩效有影响。通过比较学历和职称两个维度衡量的人力资本质量结果，可以研究专用型与通用型人力资本在企业创新绩效中的作用。

值得强调的是，本文进行的上述分解在数学上是完备的，而其经济解释也相对独立，因此可作为一组变量综合考察人力资本对创新绩效的影响。实证部分会分别用研发人员受教育总年限以及分解一、分解二各变量作为核心自变量进行回归，并比较这3种结果。

为了消除跨层次影响的干扰，对创新网络及其交互效应进行了控制。本文采用企业创新合作伙伴个数这一指示变量。该变量来自上海科委对受调查企业的问卷问题，询问企业主要且持续的技术创新合作伙伴个数及所在区域。本文将企业依照创新合作伙伴数量的多寡分为四种类型：无创新合作伙伴、1个合作伙伴、2个合作伙伴、3个及以上合作伙伴。企业合作伙伴越多，企业的创新网络密度越大，企业的合作行为越密集。

此外，本文还对科技活动经费支出、委托外单位开展科技活动支出这两项研究经费支出进行控制。根据ROTHAERMEL和HESS［4］的三层次模型，R&D经费支出、研发人员雇佣与激励与创新成果高度相关。同时，本文对企业规模（总资产和主营业务收入）、高新技术产品收入、企业净利润也进行控制。此外，为了控制政企关系，还控制了高新企业的认定以及税收优惠这一政策因素。最后，对企业所处的行业及区域进行控制，行业的分类依照《国民经济行业分类》（GB/T4754-2011）合为7类行业②本文将制造部门与能源建筑业归为制造业，将流通部门、生产服务部门、科学文化及公共事业归为服务业，其余分类不变。，地区分为上海核心区、次中心城区、近郊区及远郊区③具体划分方式为：核心区包括黄埔、静安、闸北（现归入静安）；次中心城区包括虹口、浦东新区、普陀、徐汇、杨浦、长宁；近郊区包括宝山、嘉定、闵行；远郊区包括崇明、金山、青浦、松江、奉贤。。

本文还选择了研发经费支出、总资产、主营业务收入的一阶滞后项作为控制变量，同时控制了因变量的一阶滞后项。JACOBSON［53］认为添加回归自变量的滞后项会使估计结果更加保守，并能有效控制模型设定偏误，而对创新成果的滞后可有效控制企业规模及历史研发水平。

2.3 数据描述

本文按照企业主营业务收入中位数将样本分为小型企业和大型企业；按照上文分类标准将企业分为制造型企业与服务型企业。对全样本和各子样本进行描述性统计，比较样本之间因变量、自变量、企业规模、盈利水平、企业外部关系的不同，并对各子样本之间的包含关系进行分析。具体结果见表1。

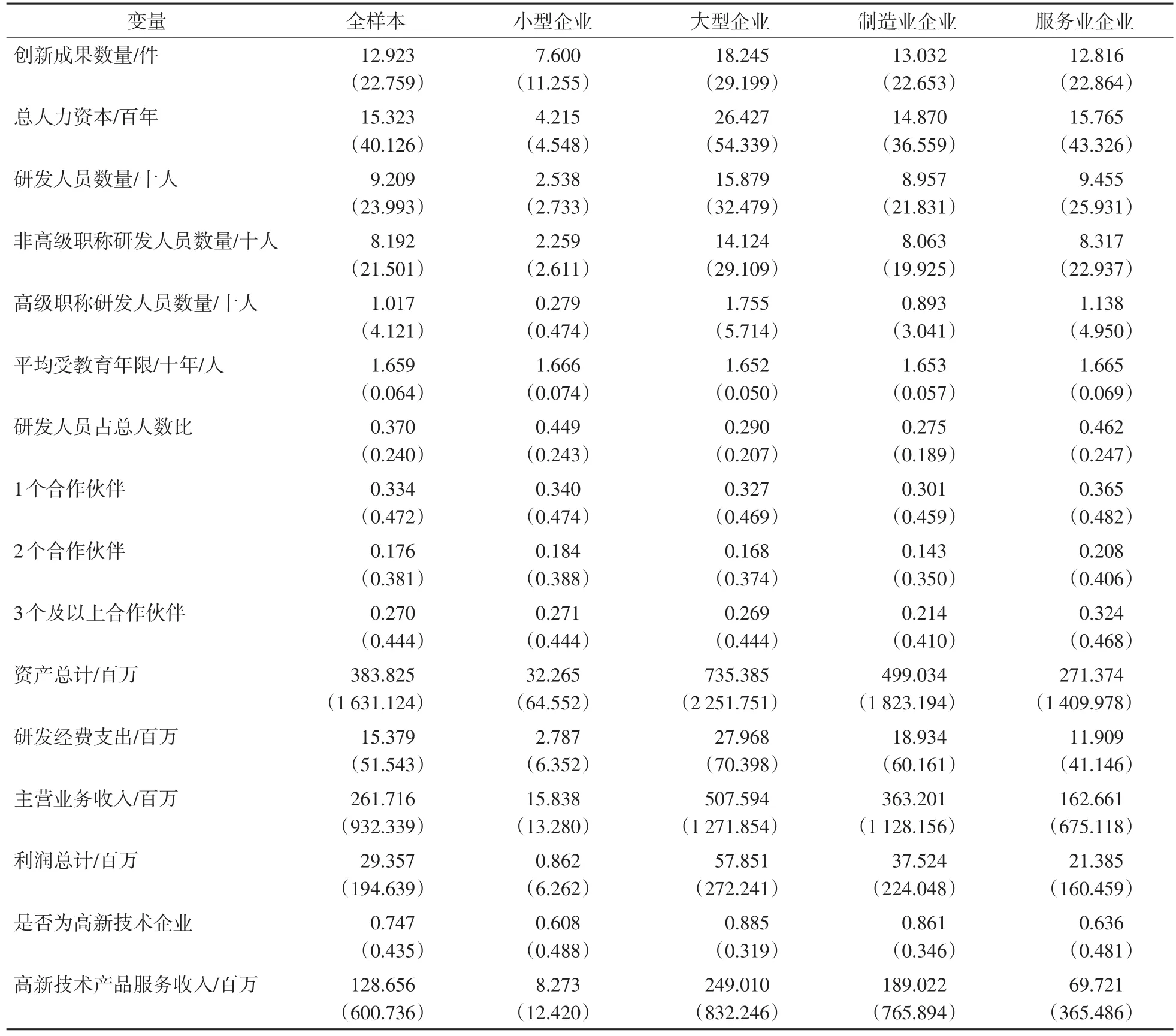
表1 各样本描述统计结果Tab.1 Descriptive statistics for the sample and subsample

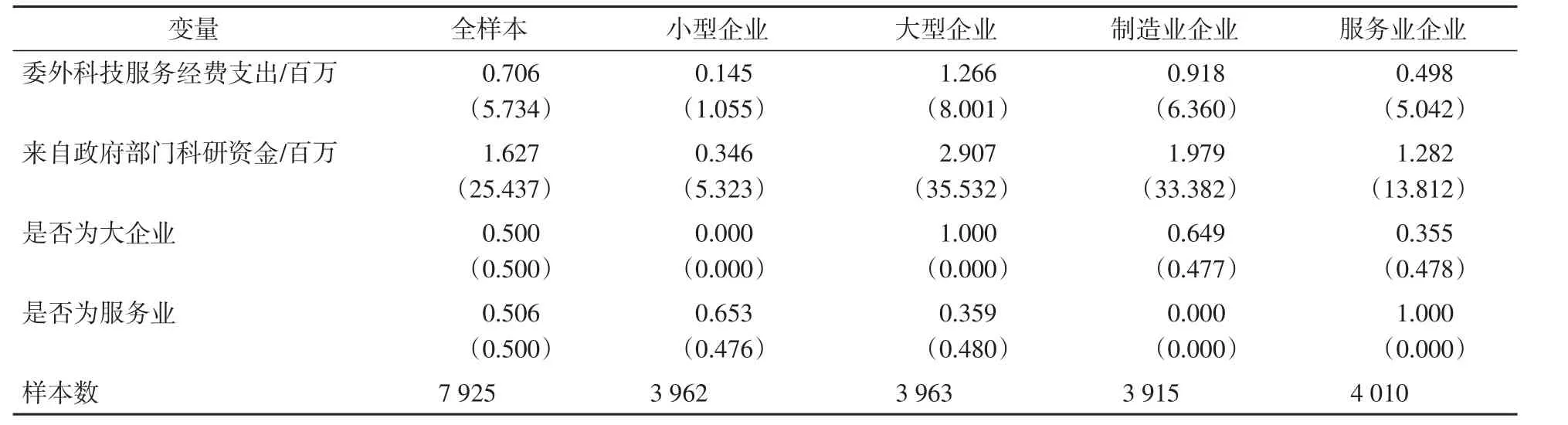
续 表

如表1所示，全样本中的制造业与服务业企业数量基本相当，制造业中64.9%为大企业，而服务业中仅35.5%为大企业，小企业中服务业占比65.3%。

值得注意的是，按行业分类与按企业规模分类的样本重合度过高，可能导致对回归结果解释困难，即按行业分类的回归结果差异可能不是由行业差异造成的，而是由样本主成分（即规模）的差异造成的。但本文观察到尽管制造业中大企业较多，服务业中小企业较多，一些重要的自变量（如人力资本总量、数量、质量、结构以及合作伙伴个数）的大小关系与样本的主要成份（即大企业和小企业）的大小关系并不相符。比如，大企业人力资本总数为小企业的近7倍，研发人数是小企业的近6倍，但这两个指标在服务业与制造业企业间几乎相同。本文认为服务业与制造业之间对比回归将会呈现不同于按企业规模分类回归的新规律，因此，按行业分类是有意义的。

3 估计策略

本文的回归均基于以下创新方程，具体表达式为

其中，被解释变量Yi为企业创新成果数量，方程（1）中的人力资本以人力资本总量（THCi）度量，方程（2）中将人力资本分为研发人员数量（NHCi）、平均人力资本（AHCi）和研发人员占比（SHCi）3个变量，方程（3）中lNHCi表示非高级职称研发人员数量，hNHCi表示高级职称研发人员数量。Xi表示控制变量；ei为随机误差项。

因变量创新成果数量是非负的整数变量，针对这种类型的因变量，可以采用“加1后取对数”方法、泊松回归及负二项回归。其中，对数回归法相对粗糙（在贸易相关研究中较为常用），回归结果一般仅作为参考对照；而针对专利等创新成果有明显的过度离散分布的情况，负二项回归相较泊松回归可以更好地拟合数据④泊松回归假设变量的均值和方差相等，而本文对因变量的假设检验显示变量存在过度离散的分布，因此泊松分布不适用。，并能对遗漏变量、异方差有较好地处理效力［54］。本文对因变量分布进行检验，在全样本中，因变量均值为12.92，方差为22.76，未通过均值与方差相等的假设检验。此外，对全样本回归结果采用LR检验过度分散参数，置信区间为1.03～1.18，拒绝原假设，故认为负二项回归是更合适的估计方式。因此，本文主要采用负二项回归，并将其与非面板（pooled）的回归结果对照。

固定效应及随机效应都可以控制面板数据的内生性，本文采用Hausman检验对两种模型的效力进行比较，从结果上来看，最终选择了随机效应模型，同时观察到类似文献［4］也采用了随机效应模型。在此基础上，为了防止其他未观测到的内生性，将规模变量（研发经费支出、总资产、主营业务收入）和因变量做了一阶滞后处理。

本文首先对全样本分别按总人力资本的两种分解方式进行回归，探究人力资本各个要素对创新绩效的影响；为了进一步探究不同企业条件（规模、行业）下人力资本的效力，将样本按收入分成大型和小型企业，按行业分成制造业和服务业企业，分别回归比较人力资本影响。通过以上步骤，本文将回答以下问题：人力资本对创新绩效的影响是否为正？创新效应主要是由哪部分贡献（数量、质量、结构）？对于创新人力资本的数量与质量，是“以质取胜”还是“以量取胜”？创新人力资本存在规模效应还是偏态分布？对于创新人力资本质量的影响，学历因素和职称因素哪个更重要？是否存在明星科学家效应？创新人力资本在不同的企业阶段和行业中更强调专用性还是通用性？

4 估计结果

4.1 全样本估计结果

在全样本条件下，以创新成果数量为因变量、人力资本总量及各分量（对应分解一和分解二）为自变量进行负二项回归，并控制创新伙伴个数等控制变量。此外，本文对负二项回归模型进行了Hausman检验，为避免异方差问题，一并对检验采用自助法修正。对于以总人力资本为自变量的方程（1），卡方值为6.62，以各人力资本分量为自变量的方程（2），卡方值为12.38，均不能在10%的显著性水平下拒绝原假设，因此采用随机效应模型得出的结果更加有效。下文所有表格中的结果均为回归系数值，但在结果分析中会将系数转换为更有经济意义的发生比率（incidence rate ratio，IRR）调整值⑤即结果会以自然常数e为底，回归系数为指数，计算其对应的IRR值，而(IRR-1)则表示该变量对因变量的贡献比例。。

全样本的核心结果为表2的分解一、分解二，而对于人力资本总量（未进行分解）的负二项回归结果（模型1和模型2）将作为正式结果的对照。本文将未添加与添加控制变量的结果进行对照，以检验控制变量的效力。

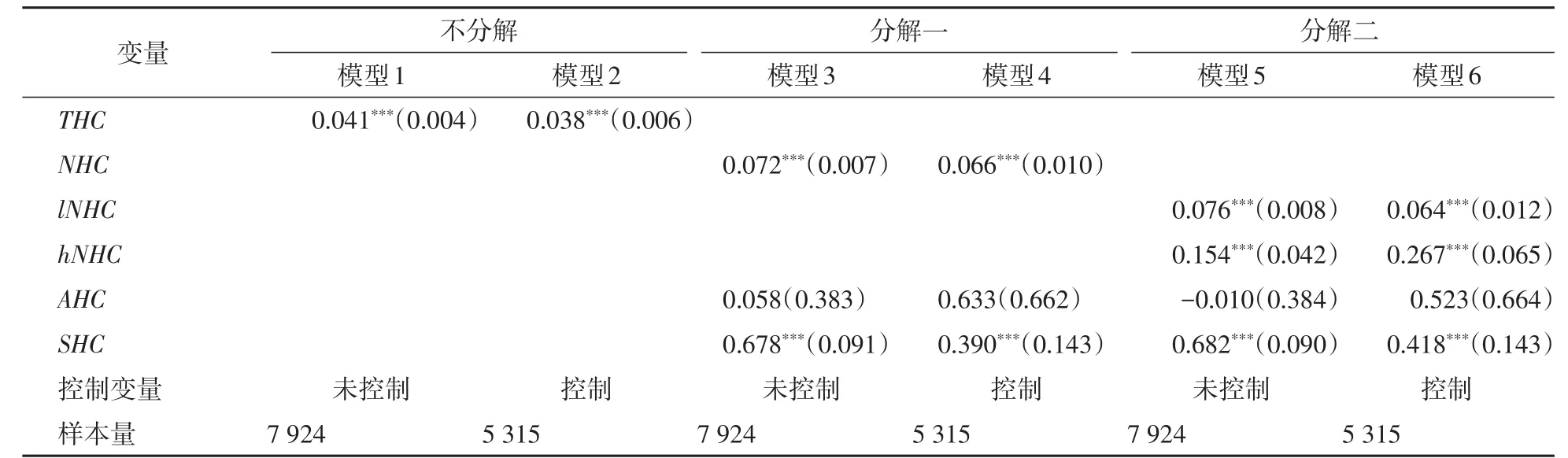
表2 全样本负二项回归结果Tab.2 Regression results of negative binomial estimation on the total sample

模型1和模型2是总人力资本的回归结果，模型1中未添加控制变量，模型2则添加了所有的控制变量。结果显示，添加控制变量前后总人力资本的影响依旧显著而数值上略有下降，这说明对于全样本而言，人力资本明显对创新绩效有正向贡献（3.8%）。模型3和模型4采用第一种方式对人力资本各个要素进行了分解，结果显示，人力资本的数量及结构对全样本的创新绩效影响更为显著，而质量的影响不显著，即人力资本对创新绩效的正向贡献可以分解为人力资本数量（每百人）7%及人力资本结构（每10%）4%，而人力资本质量（以学历衡量）无显著影响⑥均已做IRR调整，后面各结果的分析也同样处理，之后不再赘述。。模型5和模型6的结果表明，无论是高级职称还是非高级职称的研发人员数量均对创新绩效有显著影响，且具有高级职称研发人员的贡献（31%）约为具有非高级职称研发人员（7%）的4.7倍，这说明以职称衡量的人力资本创新贡献存在明显的偏态分布。

综上，针对全样本回归模型，本文得出以下结论：①对于上海科技型企业，总人力资本的作用明显，具体是由于人力资本数量和结构的差异导致；②无论是人力资本数量还是结构，都是对人力资本规模的衡量，这似乎说明企业对创新人员的投资应该“以量取胜”，人力资本对创新绩效的作用有很强的规模效应；③以学历衡量的人力资本质量差异对创新绩效影响不明显，以职称衡量的人力资本质量差异对创新绩效影响显著，这说明在人力资本质量对企业创新绩效影响这一问题上存在较大分歧。为了进一步解释全样本的回归结果，下文将样本按照规模和行业进行分类，可更加细致地观察各样本下的不同结论。

4.2 按企业规模分类的子样本结果

本文按照企业主营业务收入中位数将样本分为小型企业和大型企业，分别对两类样本进行回归，结果如表3所示。对于总人力资本，两类企业都显示了较为显著的正效应，且小型企业人力资本贡献的绝对值更高。对于小型企业，企业人力资本每千年的教育年限增长，将每年贡献137%的创新成果；对于大型企业，这一数值降到了12%。

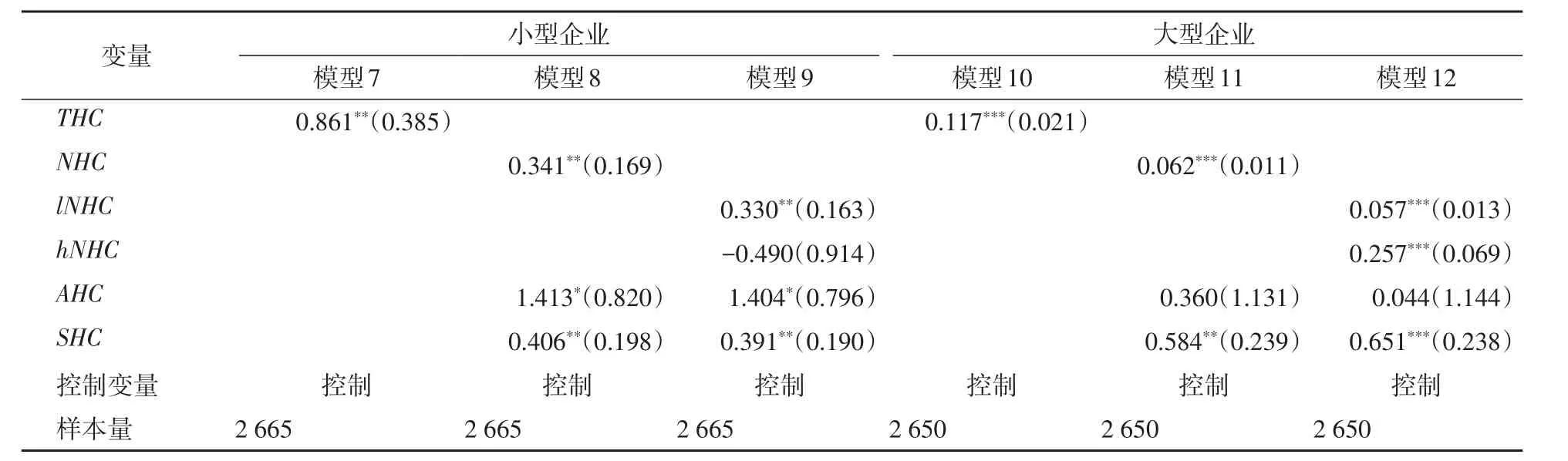
表3 按企业规模分类的子样本负二项回归结果Tab.3 Regression results of negative binomial estimation：by different scale

模型8和模型10表明人力资本数量和结构的回归结果与全样本一致，两者均为影响企业创新绩效的主要变量。此外，人力资本数量对小企业的贡献显著强于大企业，但人力资本结构对小企业的贡献则弱于大企业，即对于小企业，每增加百名研发人员，企业每年将提高创新产出41%，而大企业仅为7%；保持其他变量不变，对于小企业，研发人员每增加10%，创新产出可提高5%，而大企业则为8%。值得注意的是，人力资本质量的相关结论与全样本不同：对于小企业，人力资本质量对企业创新绩效同样有正向作用，研发人员的教育年限每提高一年，创新产出将提高311%；对于大企业，人力资本质量（以学历衡量）的贡献不显著。这一结果说明人力资本对所有企业并非都是单纯“以量取胜”，对小规模企业来说，人力资本质量（以学历衡量）则非常重要。

对人力资本进一步进行分解，模型9和模型12的回归结果如下：对于小企业，以学历衡量的人力资本质量（即平均人力资本）对企业创新绩效有显著的正向影响，而以职称衡量的人力资本质量（即高级职称研发人员数量）对企业创新绩效无显著影响，回归数值甚至为负数；而对于大企业，这一结论相反，以职称衡量的人力资本质量（即高级职称研发人员数量）对企业创新绩效有显著正向影响。这一结果说明，对于小企业的创新，更重要的是研发人员的平均学历，即研发人员的通用知识与能力，而所谓“明星科学家”的效应并不突出；对于大企业，“明星科学家”效应尤为重要，研发人员的通用知识与能力反而并不能更多助力于企业创新。

对于这一结论，KLAAS等［55］的研究表明，小企业常常依赖创始人的知识与技能，使得非管理层研发人员的创新作用被相关文献系统性低估；而ANDRIES与CZARNITZKI［29］认为，对于小企业，基础研发人员对创新绩效展现出很强的促进作用，且这种作用是和研发人员参与的创新类型相关（相比于过程创新，基础研发人员更适合在产品创新中发挥作用），他们建议小企业应考虑自身的创新类型，并让更多的基础研发人员参与创新而非局限于几个顶尖的研发人员或管理者。本文认为小企业创新中更多是突破性产品创新，需要知识转移能力并非线性地进入其他知识领域，因此需要具备较强通用知识与能力的人才，回归结果也显示出中小企业创新更需要较高的研发人员平均学历；而大企业创新中更多的是渐进性的过程创新，需要具备较强专用知识与能力、经历较长实践的人才，因而研发人员的专用性知识与能力对于企业创新尤为重要。这一结论和吴爱华和苏敬勤［2］的研究结论较为一致。此外，“明星科学家”效应在大企业中更加突出，主要原因是顶尖科学家所谓的“看门人（gate keeper）”“锚（anchor）”的作用是建立在成熟的研发体系与研发方案上的，从某种意义上来讲也是渐进式创新的一部分。

综上，人力资本分解一和分解二的结果说明，人力资本数量、结构、质量对不同规模企业的创新绩效均有非常重要的影响，但这种影响在不同企业中表现不同。对于小规模企业，通过学历衡量的通用型人力资本质量差异更加重要，而对于大规模企业，则存在更明显的“明星科学家”效应，专用型的高质量研发人才更加关键。

4.3 按行业分类的子样本结果

本文将企业按制造业和服务业分成两组，回归结果如表4。通过上文可看出，服务业企业多为小企业（64.5%），而制造业企业多为大企业（67.7%）。除企业规模外，两类样本其他变量差距不大（包括创新成果数量、单位资产对应人力资本、平均受教育年限、合作伙伴数量等）。将回归结果与按企业规模的回归结果进行对照，发现制造业（服务业）关于人力资本、合作伙伴的特性与大企业（小企业）并不完全一致，据此认为按照行业分类的回归是有意义的，其反映的规律与企业规模并无直接关系。

表4 按行业分类的子样本负二项回归结果Tab.4 Regression results of negative binomial estimation：by different industries

首先，总人力资本对创新绩效的作用非常明显，且在制造业企业中，人力资本对创新绩效的影响更为明显，是服务业的近三倍⑦可以看到大企业人力资本总量系数的绝对值远低于小企业，而多为大企业的制造业却在这一数值上是服务业的3倍。这进一步说明了行业子样本的回归结果并非是企业规模导致的，这部分结果反映了新规律。。其次，对于制造业来说，研发人员与制造、后勤人员的比例并不能对创新绩效有显著影响，这可能与制造业企业的较多创新来自“干中学”的实践有关，且较多创新需要后勤人员支持。而在服务业企业中，研发人员占比越大，越能促进创新成果产出，这一点也较符合预期。最后，制造业企业似乎更加“以量取胜”，从模型14和模型17对比来看，其研发人员数量对创新的贡献是服务业的3倍以上（13%对4%）。

两种分解的结果可以更加清楚地解释这一问题。首先，制造业企业呈现出更明显的“规模效应”特征，即使对于更加细致的分解二，通过对比模型15和模型18，也得出了制造业企业非高级职称研发人员数量的贡献是服务业企业的近3倍（13%对5%）、高级职称研发人员数量的贡献是服务业企业的7倍（70%对10%）这一结论。其次，制造业企业与服务业企业的人力资本质量均对企业创新绩效有正向影响，但其贡献方式并不一致，对比模型15和模型18可知，服务业企业研发人员的平均学历非常重要，其对创新绩效的影响远高于制造业企业；而制造业企业则更关注研发人员的职称等级。这说明“明星科学家”效应在制造业中起到更大的作用，且制造业企业相对于服务业企业更需要专用性的知识与能力。

5 结论与启示

本文将人力资本按数量、质量、结构细化，并引入学历、职称这两种人力资本质量相结合的方法进行研究，有助于全面完整地刻画出人力资本对企业创新绩效的影响。研究发现：人力资本对创新绩效的正向提升是毋庸置疑的，并且这种提升主要是由于人力资本的规模效应引起的，而在全样本中人力资本质量对创新绩效的正向提升作用有分歧（至少研发人员学历差异对创新绩效的影响不显著）。

当细化到分行业、分企业规模进行实证研究时，结论变化较大。人力资本对创新绩效的作用不仅由其规模（数量与结构）决定，也由其质量决定，但在不同环境下决定的机制不同。对于小规模企业，人力资本质量的影响主要表现为研发人员的通用知识与技能，即研发人员的平均学历对创新绩效有显著提升；而对于大规模企业，尽管研发人员平均学历的影响不显著，但人力资本质量通过研发人员的专用知识影响创新绩效，即大型企业更需要职称高的有经验、有专用性知识与能力的研发人员，从而发挥“明星科学家”效用。对于制造业企业，人力资本的“规模效应”强于服务业企业，且研发人员的职称对创新绩效有显著提升；而服务业企业则需要研发人员有更高的平均学历。

本文的实证研究表明在一般意义上人力资本对创新的作用可以仅用人力资本的“规模效应”来表征，也说明在众多经济模型中⑧比如ROMER［56］的内生增长模型、GRILICHES［8］的创新函数等。仅考虑研发人员的数量是相对合理的。此外，本文为人力资本专用性与创新过程的联系提供了实证依据，是对产品创新理论及人力资本专用性理论的有效补充。研究说明了人力资本质量差异在不同行业、不同企业规模下的作用机制不同，而人力资本的通用与专用性理论可以有效解释该作用机制，即学历反映人力资本的通用知识与技能差异，而职称差异反映专用知识技能及经验的差异，正如前文所述，专用型研发人员与渐进式创新更相关，而通用型研发人员与突破式创新更相关。对于小规模企业或是服务业企业，突破式产品创新在企业创新中所占比例更大，因此更需要通用型人才；而对于大规模企业或是制造业企业，渐进式过程创新在企业创新中所占比例更大，因此更需要专用型人才。同时，“明星科学家”效应更容易出现在渐进式过程创新中。

最后，本文的结论对企业自身战略决策、人才培养与政府人才引进政策均有启发意义。创新企业在对人力资源进行规划时，应该充分考虑企业自身情况，尤其是企业创新的过程（渐进创新还是突破创新），不应盲目扩充人员数量或者聘请所谓的高端人才。对于制造业类企业或成熟企业，创新人才在企业渐进式创新中的“规模效应”以及“明星科学家”效应更明显，企业可以通过扩大创新人才数量、雇佣顶尖的高职称人才来有效提升创新绩效。而对于服务业企业或初创企业，高学历的通用人才会对企业的突破式产品创新有更大贡献，人才平均学历与素质对创新绩效的提升更有效。此外，政府在高学历人才和高技术人才的引进政策上，也可参照本文研究结论进行分行业、分部门的细化，进行“精准引才”，做到“人尽其才，才尽其用”。

本文样本是上海市的科技企业，对全国一线城市中的科技企业有一定代表性，并体现了中国创新最活跃地区之一的创新情况与规律。出于数据口径和一致性的考虑，样本截至2015年末，对于在新形势下结论是否发生改变，以及人力资本要素在新兴的创新过程中是否有新的作用机制，都值得在未来的研究中进一步探讨。