双曲线的基圆及其性质
2020-09-09陕西省汉中市镇巴中学723600刘再平
陕西省汉中市镇巴中学(723600) 刘再平
陕西省汉中市龙岗学校(723000) 唐宜钟
定理在平面直角坐标系Oxy下,对于任意给定的双曲线R2为其基圆,则有:
(1)圆O基的切线交双曲线两支于A、B两点,则OA⊥OB;
(2)设A、B是双曲线C两支上的动点,OP⊥AB且P为垂足,若OA⊥OB,则点P的轨迹就是圆O基;
(3)设A、B是双曲线C两支上的动点,若OA⊥OB,则线段AB长的最小值为2R,三角形AOB面积的最小值为R2;
(4)过双曲线的中心且互相垂直的两条直线与双曲线的四个交点构成的四边形为棱形,且棱形的内切圆就是该双曲线的基圆.

图1
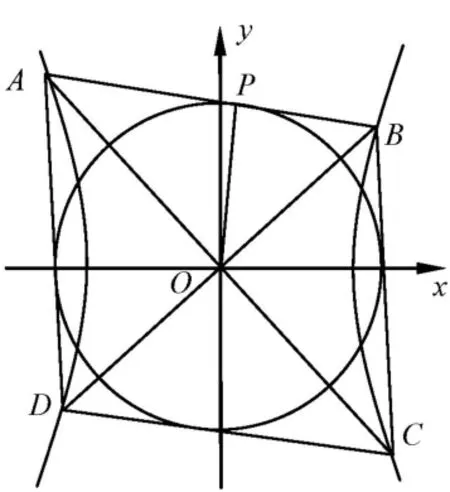
图2
证明(1) 设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),即y1=kx1+m,y2=kx2+m,则

又直线y=kx+m与O基:x2+y2=相切,即则m2(b2-a2)=(1+k2)a2b2,将直线AB方程与双曲线方程联立:消y得:(b2-a2k2)x2-2a2kmx-a2m2-a2b2=0,所以

即

故OA⊥OB.
(2)设直线OA方程为y=kx,A(x1,kx1),将直线OA方程与双曲线联立:得即所以

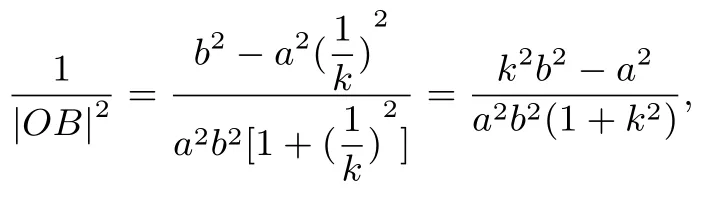
所以

即|OP|=R,所以点P的轨迹就是以原点O为圆心,R为半径的圆O基:x2+y2=R2.
(3)由(2)

则
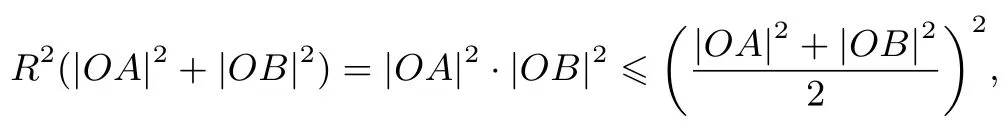
当且仅当|OA|=|OB|时取等号,即|OA|2+|OB|2≥4R2.
根据题意OA⊥OB知|AB|2=|OA|2+|OB|2,所以|AB|2≥4R2,故|AB|≥2R,即SΔAOB=|AB|·|OP|≥·2R·|OP|=R2.
(4)如图2,根据双曲线关于原点的中心对称性,即OA=OC,OB=OD,则四边形ABCD为平行四边形,由AC⊥BD,所以四边形ABCD是棱形,又根据(2)可直接推出棱形ABCD的内切圆就是该双曲线的基圆.
从上述性质的生成与证明过程中,不但能够加深我们对其数学本质的理解,而且还能感受到数学的简洁美、严谨美与和谐美.
